Dass an einem Ort immer nur ein Gegenstand sein kann, ist für uns ziemlich selbstverständlich. Wenn wir etwas greifen, funktioniert das, weil unsere Hand nicht in den Gegenstand eindringt, wenn wir auf dem Boden stehen, dann fallen wir nicht durch den Boden durch, weil eine Kraft uns daran hindert. Fragt sich nur, was das eigentlich für eine Kraft ist und woher sie kommt. Überraschenderweise braucht man die Regeln der Quantenmechanik (kurz QM), um wirklich zu verstehen, warum wir nicht durch den Boden fallen.
Atome
Alle Materie besteht aus Atomen. Man kann sich Atome einfach als kleine harte Kügelchen vorstellen, die sich anziehen können (deshalb sind unser Fuß und der Boden Festkörper), die sich aber auch abstoßen, wenn sie sich zu nahe kommen. Dass wir nicht durch den Boden fallen, liegt also daran, dass die Atome im Boden die Atome in unseren Füßen abstoßen, wenn sie sich nahe genug kommen.(Eine Bindung gibt es zwischen ihnen nicht, weil die Atome in Füßen und Boden schon vollständig gebunden sind und keine weiteren Bindungen eingehen können.)
So weit, so einfach. Aber es stellt sich natürlich die Frage, woher eigentlich diese Abstoßung kommt. Und da fängt es durchaus an, kompliziert zu werden.
Energieniveaus
Objekte im Alltag können beliebige Energien haben. Ich kann einen Ball hochheben, dabei ändert sich seine Energie im Schwerefeld der Erde (potentielle Energie) oder ich kann ich werfen, dabei ändert sich seine Bewegungsenergie. Die Energie kann dabei beliebige Werte annehmen. [Expertinnenhinweis: Ja, natürlich hat der Ball eine Ruhemasse, die einer Energie entspricht und die ich nicht einfach ändern kann und ja, natürlich kann man das Verhalten im Schwerefeld genauer mit der Allgemeinen RT beschreiben, aber diese Feinheiten sind heute irrelevant.]
Elektronen, die an einen Atomkern gebunden sind, können nur ganz bestimmte Energien haben, nicht beliebige Werte der Energie. (Mit Hilfe der Quantenmechanik kann man auch verstehen, warum das so sein muss.) Hier ein Diagramm der Energieniveaus im Wasserstoff (geklaut in meinem Buch “Funktionswerkstoffe”):
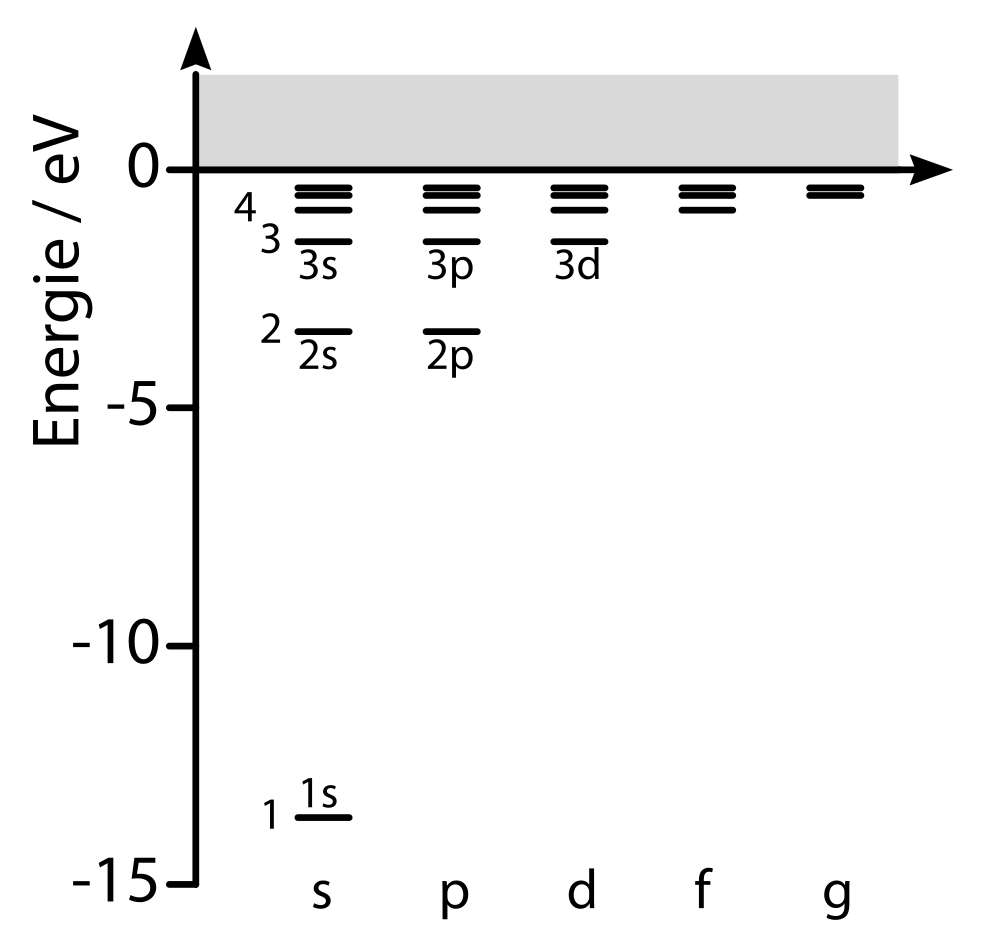
Auf den ersten Blick sieht das kompliziert aus, aber wir brauchen zum Glück nicht alle Details. Wichtig ist nur, dass nur bestimmte gebundene Zustände für ein Elektron möglich sind, die durchnummeriert werden (von 1 bis unendlich). Alle diese Zustände sind gebunden, deshalb zählt man ihre Energie negativ. Die Energie ist dabei in Zuständen mit niedrigerer Zahl kleiner (die Elektronen sind stärker gebunden). Zustände mit Energie größer als Null gibt es auch, die sind dann aber nicht gebunden und das Elektron kann sich beliebig vom Atomkern entfernen. Das ist das graue Band oben. Die Skala links misst einfach die Energie in einer Einheit namens “Elektronenvolt”. Weil nur ganz bestimmte Energien möglich sind, spricht man auch davon, dass die Energie “quantisiert” ist – sie kann sich nur in ganz bestimmten Mengen ändern, nicht beliebig.
Die unterschiedlichen Buchstabenkürzel (s,p,d,f usw) kennzeichnen verschiedene Zustände; für die Energie ist aber nur die Nummer des Zustands relevant – die Zustände 3s, 3p und 3d haben alle dieselbe Energie. (Das ändert sich dann, wenn man mehrere Elektronen hat wie bei anderen Atomen, dann verschieben sich diese Energieniveaus ein wenig, das habe ich mal in diesem Artikel erklärt.)
Wie sieht so ein Zustand aus? Im berühmten Bohrschen Atommodell, das ihr vielleicht in der Schule kennengelernt habt, wurde angenommen, dass die Elektronen auf Kreisbahnen um den Atomkern sausen wie Planeten um die Sonne. Das ist allerdings zu vereinfacht, denn in der QM beschreibt man die Elektronen nicht einfach als ein punktförmiges Teilchen, sondern eher als eine Art Elektronenwolke (die man auch “Orbital” nennt).
Wenn ihr genau wissen wollt, was es mit dieser Wolke auf sich hat, empfehle ich die QM-Artikel aus meinen Artikelserien. Für heute reicht zu wissen, dass man sich ein Elektron so vorstellen kann, als wäre es über einen gewissen Bereich “verschmiert”, es lässt sich nicht genau lokalisieren, ein bisschen wie Wasser, das in Form von Nebel vorliegt. Je mehr ihr versucht, das Elektron an genau einem Punkt festzunageln, desto höher ist die Energie des Elektrons. Das lässt sich auch über die berühmte Unschärferelation verstehen (wenn euch das nichts sagt, ignoriert dieses Argument einfach…): Wenn man den Ort eines Elektrons sehr genau kennen will, dann ist seine Geschwindigkeit unbestimmt (ähnlich wie der Ort nicht eindeutig ist, ist es auch der Wert der Geschwindigkeit nicht) und damit auch seine Bewegungsenergie.
Elektronen lassen sich also durch eine Elektronenwolke beschreiben, und die hat eine um so kleinere Energie, je weiter sie ausgedehnt ist. (Das ist etwas vereinfacht, reicht aber für den Moment.) Auf der anderen Seite möchte unser Elektron im Wasserstoffatom natürlich dicht beim Atomkern sein, weil der positiv geladen ist und unser negativ geladenes Elektron anzieht. Deshalb bildet sich ein Kompromiss heraus, bei dem das Elektron sich in der Nähe des Atomkerns aufhält, aber nicht komplett in den Atomkern hineinstürzt. Dass Materie also überhaupt eine nennenswerte Ausdehnung hat, liegt daran, dass Elektronen sich nicht so gern auf einen sehr kleinen Raum einengen lassen. (In Metallen kann man allein auf dieser Basis bereits den Widerstand gegen das Zusammendrücken relativ gut abschätzen.)
Hier mal ein Bild von solchen Elektronenwolken, oben in einer Darstellung wie Nebeltröpfchen, unten als eine Art “Blob”.

Gemeinfrei, Link
Ihr seht, dass die Elektronenwolken unterschiedlich groß sein können und dass unterschiedliche Zustände wie 1s und 2p unterschiedliche Formen der Wolke haben. Der 1s-Zustand ist so dicht am Atomkern konzentriert wie möglich, deshalb hat er auch die kleinste Energie, die anderen Zustände sind weiter ausgedehnt. Dass es bei 2p drei Varianten gibt, ist eine zusätzliche Komplikation, die ignorieren wir erst mal. Die genaue Form der Elektronenwolken ist eh nicht so wichtig, wichtig ist nur, dass die Elektronenwolke nicht beliebig um den Atomkern angeordnet sein kann.
Atome auf Kollisionskurs
Nehmen wir als Beispiel zwei Atome des Heliums. Ein Heliumatom hat zwei Elektronen, die beide im Zustand 1s sind, also eng an das Atom gebunden in einer schönen Elektronenwolke. Jetzt schieben wir die beiden Atome aufeinander zu. Was hindert die Elektronenwolken daran, sich zu durchdringen? (Helium ist natürlich insofern kein gutes Beispiel, weil Helium keinen Festkörper bildet, aber es macht das Prinzip leichter zu verstehen, wenn wir uns mit möglichst wenig Elektronen beschäftigen.)
Zum einen spielt hier die elektrische Ladung der Elektronen eine Rolle: Elektronen sind negativ geladen und die Elektronenwolken stoßen sich deshalb ab. Das kann man auch ohne QM verstehen, gleiche elektrische Ladungen stoßen sich ja auch laut den Regeln der klassischen Physik ab. Das ist aber nicht das ganze Geheimnis, in Wahrheit ist die Sache komplizierter. Wenn die Elektronen nämlich tatsächlich wie eine Wolke um den Atomkern herum angeordnet sind, warum verformen sich die beiden Wolken nicht einfach ein wenig, so als würde man zum Beispiel zwei Kissen aneinander vorbeiquetschen?
Es ist prinzipiell möglich, Elektronenwolken zu verformen, aber sobald man das tut, ist das Elektron eben nicht mehr im Zustand 1s, sondern in einem anderen Zustand. Dieser Zustand hat dann eine höhere Energie, entsprechend bräuchte man eine große Kraft, um die Elektronenwolken wie Kissen aneinander vorbei zu quetschen. [Expertinnenhinweis: Ihr könnt einen passenden Überlagerungszustand aus den einzelnen Zuständen basteln, bei dem die Elektronen z.B. stärker auf der einen oder anderen Seite konzentriert sind. Beispielsweise könnte man zum 1s-Zustand den 2p-Zustand addieren, der hat ja auf einer Seite ein negatives Vorzeichen und damit würde insgesamt der Wert auf dieser Seite verringert. Der Zustand ist dann, weil ihr unterschiedliche Eigenzustände kombiniert, kein Energieeigenzustand mehr und damit auch zeitabhängig, das wäre hier aber ja o.k., weil wir ja zwei Atome gegeneinander bewegen wollen. Wichtig ist hier nur, dass die Energie (bzw. deren Erwartungswert) bei dieser Aktion deutlich ansteigt.]
Ist das also die Antwort auf unsere Frage, warum wir nicht durch den Boden fallen? Ja, aber es ist nicht die ganze Antwort.
Elektronenwolken und Bindungen
Wir können Elektronenwolken also nicht einfach beliebig verformen. Verändern sie sich also gar nicht, wenn wir die Atome zusammenbringen? Doch, das tun sie. Um das zu sehen, vereinfachen wir die Situation noch weiter. Statt zwei Helium-Atomen mit vier Elektronen betrachten wir zwei Wasserstoff-Atomkerne (also zwei Protonen) und erst mal nur ein Elektron. Das Elektron kann an den einen oder an den anderen Wasserstoffkern gebunden sein, seine Energie ist jedes mal dieselbe und es ist im 1s-Zustand von oben.
Schieben wir die beiden Wasserstoffkerne zusammen, dann überlagert sich deren elektrisches Feld. Es ist deshalb energetisch günstiger, wenn wir etwas mehr elektrische Ladung in der Mitte zwischen den beiden Protonen haben, wenn dort also die Elektronenwolke etwas konzentrierter ist. Die beiden 1s-Zustände kombinieren sich damit zu einer gemeinsamen Elektronenwolke, das sich über beide Atomkerne erstreckt und das man sich etwa so vorstellen kann:

Von derivative work: Pbroks13 (talk)
Dihydrogen-HOMO-phase-3D-balls.png: Benjah-bmm27 – Dihydrogen-HOMO-phase-3D-balls.png, Gemeinfrei, Link
Expertinnenhinweis: Erscheint euch das widersprüchlich? Oben habe ich gesagt, ich einen Zustand darf nur aus den vorhandenen Energieeigenzuständen zusammenmischen und Zustände mit höherer Energie als 1s würden die Energie erhöhen. Ich kann also nur die beiden 1s-Orbitale kombinieren, aber wieso kann sich dabei die Energie ändern? Der Grund ist simpel: In der Tat addiere ich einfach die beiden Wellenfunktionen (die Methode nennt man generell auch LCAO – linear combination of atomic orbitals), aber die Wahrscheinlichkeit, das Elektron irgendwo zu finden, ist ja das Quadrat der Wellenfunktion. Wenn ich also zwei Wellenfunktionen addiere, ist die Aufenthaltswahrscheinlichkeit in der Mitte entsprechend erhöht. (Ist der mittlere Wert der WF in einem Raumbereich 0,1 [in irgendwelchen Einheiten], dann ist die Wahrscheinlichkeit, das Elektron dort zu treffen, proportional zu 0,01; wenn ich die beiden Wellenfunktionen addiere, habe ich einen Wert von 0,2 und für die Wahrscheinlichkeit entsprechend 0,04.)
Wenn wir also die beiden Wasserstoffatomkerne zusammenbringen, dann verteilt das eine Elektron seine Elektronenwolke über beide Atomkerne. Das ist energetisch günstig, weil wir sozusagen “mehr Elektron” zwischen den Atomkernen haben, und das führt dann zu einer Bindung der beiden Kerne. Um sie voneinander zu trennen, bräuchten wir Energie.
Nehmen wir ein zweites Elektron dazu, dann tut dieses Elektron dasselbe: Es setzt sich ebenfalls in den neu entstandenen Zustand, beide Elektronen sind bevorzugt zwischen den Atomkernen und sorgen für eine Bindung. Entstanden ist ein Wasserstoff-Molekül, kurz H2.
Das Pauli-Prinzip
Zurück zu unseren Helium-Atomen. Von denen hat ja jedes zwei Elektronen im 1s-Zustand, wenn sie weit entfernt sind. Können die nicht alle eine gemeinsame Elektronenwolke bilden und sich alle bevorzugt zwischen den Atomkernen aufhalten? Das wäre doch energetisch auch sehr günstig.
Das funktioniert leider nicht, und zwar wegen des sogenannten Pauli-Prinzips. Das Pauli-Prinzip sagt, dass zwei Elektronen niemals im selben Zustand sein können. Es können nie zwei Elektronen genau denselben Zustand einnehmen. Es passen trotzdem zwei Elektronen in den 1s-Zustand, weil Elektronen eine zusätzliche Eigenschaft haben, die man “Spin” nennt – der Spin kann zwei Werte annehmen, deshalb kann man zwei Elektronen in den 1s-Zustand stecken, eins mit dem einen Spinwert, eins mit dem anderen. (Etwas ausführlicher habe ich das hier erklärt. Das Prinzip gilt übrigens auch für Protonen und Neutronen, die Bausteine von Atomkernen)
Unsere günstige, bindende Elektronenwolke hat nur Platz für zwei Elektronen. Was ist mit den beiden anderen? Vorher hatten wir doch zwei getrennte Helium-Atome mit jeweils einem 1s-Zustand, also Platz für 4 Elektronen, wieso haben wir jetzt nur noch Platz für 2?
Unsere bindende Elektronenwolke haben wir gebastelt, indem wir die beiden 1s-Wolken so kombiniert haben, dass sie sich in der Mitte überlagern. Man kann die Wolken aber auch anders überlagern, und zwar so, dass das Elektron sich gerade besonders selten zwischen den beiden Atomkernen aufhält. (Dass das geht, kann man im Bild der Elektronenwolken leider nicht direkt einsehen.) Dieser Zustand ist natürlich energetisch nicht so günstig, denn da, wo die positive Ladung konzentriert ist, ist unser Elektron jetzt tendenziell nicht zu finden. Man nennt diesen Zustand deshalb auch “anti-bindend”.

Von Benjah-bmm27 – Eigenes Werk, Gemeinfrei, Link
Vorher (als die beiden Helium-Atome noch weit weg waren) hatten wir vier Elektronen im Zustand 1s, wenn wir sie zusammenschieben, dann haben wir zwei Elektronen in dem energetisch günstigen, bindenden Zustand, aber die beiden anderen passen dort nicht hinein und müssten deshalb in den energetisch ungünstigen anti-bindenden Zustand. Netto gewinnen wir dabei nichts, deshalb bildet sich so ein Zustand auch nicht aus. Wenn wir unsere Helium-Atome zusammenschieben, dann gibt es also keine Bindung zwischen ihnen.
Weil wir hier nichts gewinnen, unsere Helium-Atome aber ja negativ geladene Elektronenwolken haben, können wir sie nicht dicht zusammenbringen: Die Wolken können sich nicht ohne weiteres verformen, es können sich auch keine günstigen kombinierten Elektronenwolken ausbilden, also bleibt nur der Effekt der elektrostatischen Abstoßung übrig.
Festkörper
Nun bestehen weder unsere Füße noch der Fußboden aus Helium-Atomen. Das Prinzip ist dort aber dasselbe. Füße und Fußboden sind Festkörper, in denen wir große Verbünde von Atome (also Moleküle) haben, die alle aneinander gebunden sind, ganz ähnlich wie unser Wasserstoff-Molekül von eben. Ein Molekül bildet sich aus einer Kombination von Atomen genau so, dass die energetisch günstigen, bindenden Elektronenwolken mit Elektronen besetzt sind, die ungünstigen aber nicht. (Falls ihr in der Schule Chemie hattet: die Regeln, die ihr dort gelernt habt, stellen genau sicher, dass das so ist, so mit 8 Elektronen auf der äußersten Schale usw…) Bringt man jetzt solche Moleküle zusammen, gilt dieselbe Logik wie bei unseren beiden Helium-Atomen: Die Elektronen können nicht in gemeinsame, bindende Zustände zwischen den Molekülen gehen, weil dann auch die ungünstigen anti-bindenden Zustände besetzt werden müssten, die Elektronenwolken können sich nicht einfach verformen, weil das viel Energie kosten würde, und deshalb sorgt dann die elektrostatische Abstoßung zwischen den Elektronenwolken dafür, dass die Moleküle nicht aneinander vorbeikommen.
Es sind also gleich drei Effekte, die zusammenkommen: Atome und Moleküle haben nur endlich viele Zustände, in denen sich Elektronen aufhalten können, und diese Zustände haben eine gewisse Ausdehnung.Die energetisch günstigen Zustände sind dabei in ihrer Form genau festgelegt und können sich nicht einfach verformen. Sobald man zu viele Elektronen ins Spiel bringt, müssen Zustände mit hoher Energie besetzt werden. Das Pauli-Prinzip verhindert, dass die Elektronen alle in dieselben Zustände gehen können und die elektrostatische Anziehung sorgt dann zusätzlich dafür, dass die Elektronenwolken auf Abstand bleiben.
PS: Eigentlich wollte ich in diesem Artikel noch einige andere Alltagsphänomene erklären, die letztlich auf der Quantenmechanik beruhen. Dann habe ich aber gemerkt, dass das Problem “durch den Fußboden fallen” zum einen doch ganz schön trickreich ist und zum anderen im Internet auch auf unterschiedlichen Seiten ganz unterschiedlich erklärt wird. Einige argumentieren nur mit der elektrostatischen Abstoßung, einige nur mit dem Pauli-Prinzip. Ich habe mir hier Mühe gegeben, mein Verständnis möglichst sauber auseinanderzudröseln, habe die Erklärung in genau dieser Form aber nirgends so gefunden. Falls ihr also meint, dass hier was nicht passt, sagt bitte Bescheid.






Kommentare (36)