Es heißt ja oft, dass in unserem Alltag die klassische Physik gilt und dass Quanteneffekte normalerweise keine Rolle spielen. Für einige der besonders kniffligen Quantenphänomene wie beispielsweise die berühmte Quantenverschränkung ist das auch nicht ganz falsch, aber Quanteneffekte sind tatsächlich die Grundlage für alles, was wir im Alltag beobachten. Neulich habe ich schon gezeigt, dass sie dafür verantwortlich sind, dass wir nicht durch den Fußboden fallen.
Heute gucken wir, wie man mit einem Löffel und einer Tasse heißen Kaffee oder Tee zeigen kann, dass die klassische Physik nicht in der Lage ist, Metalle korrekt zu beschreiben.
Metalle und Elektronen
Metalle leiten ja bekanntlich Strom ziemlich gut – deswegen nehmen wir ja beispielsweise Kupfer oder Aluminium als Werkstoffe für Drähte. (Im Alltag nehmen wir meist Kupfer, aber Aluminium leitet Strom zwar etwas schlechter, ist aber auf der einen Seite billiger und auch wesentlich leichter – in Flugzeugen z.B. nimmt man deswegen auch Kabel aus Aluminium.)
Bereits kurz nach der Entdeckung des Elektrons Ende des 19. Jahrhunderts kam man auf die Idee, dass Metalle Strom leiten, weil sich in ihnen die Elektronen frei bewegen können. In einem einfachen Modell der klassischen Physik (Drude-Modell genannt) sieht das etwa so aus (lobend hervorzuheben, dass in diesem Bild Elektronen blau und positive Ladungen rot sind, wie sich das gehört, jede andere Farbkombination ist falsch!):

Von User:ARTE – Eigenes Werk, Gemeinfrei, Link
Hier seht ihr die blauen Elektronen, die um die positiven Ladungen herumflitzen. Man stellt sich vor, dass jedes Atom ein (oder auch zwei) Elektronen hat, die nur lose gebunden sind und die sich deshalb vom Atom lösen können. Zurück bleibt ein Ion – ein Atom, dem eine negative Ladung fehlt.
Wenn das so ist (so die Überlegung von Drude), dann sollten die Elektronen nicht nur Strom gut leiten können, sondern auch Wärme. Heizt man ein Ende eines Metalldrahts auf, dann werden die Elektronen dort schneller (Wärme ist ja nichts als ungeordnete Bewegung von Teilchen) und weil sie frei sind, flitzen sie dann durch das Metall und leiten die Energie weiter. Nach dieser Logik sollten also elektrische Leitfähigkeit und Wärmeleitung gekoppelt sein – Metalle, in denen die Elektronen sich besonders leicht frei bewegen können, sollten also nicht nur Strom gut leiten, sondern auch Wärme.
Und siehe da – so ist es auch. Die elektrische und die Wärmeleitfähigkeit hängen eng zusammen, das ist das sogenannte Wiedemann-Franzsche Gesetz.
Also kann man die elektrische Leitung und die Elektronen in Metallen mit den Mitteln der klassischen Physik beschreiben?
Nein, das kann man nicht. Um das zu widerlegen, braucht ihr nur eine Tasse Kaffee oder Tee zu nehmen und einen Löffel reinzustellen. (Beim Kaffee ist das eh praktisch, um Zucker umzurühren – wenn ihr Zucker in euren Tee tut, dann ist das barbarisch…) Jedes Atom in eurem Löffel sollte so etwa ein Elektron für die elektrische Leitung zur Verfügung stellen, und jedes dieser Elektronen sollte ein bisschen Wärme aus eurem Heißgetränk entziehen, wobei der Löffel wärmer wird. Die Energiemenge, die man braucht, um ein Material zu erwärmen, ist die sogenannte Wärmekapazität. Wenn jedes Elektron etwas Energie aufnehmen könnte so wie ein freies Teilchen in einem Gas und wenn jedes Atom so etwa ein Elektron abgibt, dann sind das sehr viele freie Elektronen auf relativ kleinem Raum.
Rechnet man die Wärmekapazität unter dieser Annahme aus, dann bekommt man einen Wert, der Hundert mal größer ist als der, den man bei Metallen tatsächlich misst. Euer Löffel würde dem Heißgetränk sehr viel Wärme entziehen und dabei selbst nur wenig wärmer werden und in kurzer Zeit hättet ihr nur noch ein Lauwarmgetränk.
Wir haben also einen klaren Widerspruch: Einerseits sind die Elektronen in Metallen frei und sorgen dafür, dass Strom und Wärme geleitet werden können, aber andererseits können diese freien Elektronen irgendwie nicht die Wärmemenge aufnehmen, die man eigentlich erwartet, sondern nur einen Bruchteil davon.
Das Bändermodell
Ich habe ja neulich schon erklärt, dass Elektronen in Atomen nur ganz bestimmte Werte der Energie haben können. Das ändert sich allerdings, wenn man viele Atome zusammenbringt und daraus einen großen Materialklotz macht – einen “Festkörper”. Jedes Atom bringt sozusagen seine eigenen Energieniveaus mit, aber weil die Elektronen sich ja auch zwischen den Atomen bewegen können (beispielsweise von einem zum nächsten hüpfen können), verschieben sich die Energieniveaus. Wir haben neulich schon gesehen, dass sich zum Beispiel beim Wasserstoff aus zwei einzelnen Atomorbitalen ein energetisch günstiges (bindendes) und ein energetisch ungünstiges (anti-bindendes) Orbital bildet. Wenn man jetzt viele Atome zusammenschließt, dann bildet sich eine ganze Bandbreite an Orbitalen mit unterschiedlichen Energien, die sehr dicht beieinander liegen.
Dieses Bild zeigt schematisch, wie sich die Energien ändern, wenn man die Atome zusammenschiebt (Hinweis für die ganz Genauen: schematisch deshalb, weil in Wahrheit die s- und p-Orbitale hybridisieren müssten und sich die Bänder dadurch komplizierter verschieben):

(Aus meinem Buch “Funktionswerkstoffe”)
In der linken Seite des Bildes seht ihr, wie sich Bänder ausbilden, je dichter man die Atome zusammenschiebt (“Kernabstand” ist der Abstand der Atomkerne). Sind sie weit weg, gibt es getrennte Energieniveaus, je dichter sie zusammensind, desto breiter werden die Energiebänder. Die gestrichelte Linie zeigt den Abstand, den die Atome tatsächlich haben; rechts im Bild sieht man dann die zugehörigen Energiebänder, also die Energien, die für die Elektronen bei diesem Kernabstand möglich sind. (Dabei hat im rechten Bildteil die horizontale Richtung keine Bedeutung, die ist nur, damit man schöne Bänder malen kann.)
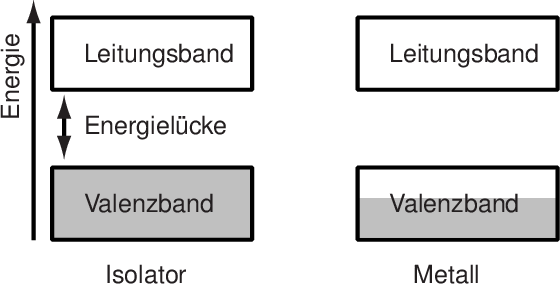
In diesem (vereinfachten) Modell kann man jetzt schon mal verstehen, warum es Metalle und Nicht-Metalle gibt. Wir besetzen jetzt die Energiebänder mit Elektronen. Dabei gilt wie beim letzten Mal das Pauli-Prinzip: Jedes einzelne Energieniveau hat nur Platz für zwei Elektronen. Wir füllen also die Bänder von unten angefangen (bei den energetisch günstigsten Zuständen) auf, bis alle Elektronen einen Platz in einem Energieniveau gefunden haben. Dafür gibt es zwei Möglichkeiten:
(Aus meinem Buch “Funktionswerkstoffe”)
Entweder in einem der Bänder sind alle Zustände gefüllt, im darüber liegenden Band keiner. Dann gibt es eine klare Lücke zwischen den gefüllten und den freien Energiebändern. Oder ein Band ist nur teilweise gefüllt so wie rechts im Bild. (Noch ein Hinweis: Die Begriffe Valenz- und Leitungsband sind meines Wissens in Metallen nicht immer ganz einheitlich definiert, man kann das halb-besetzte Band auch als Leitungsband bezeichnen, ich glaube ich habe beide Varianten schon gesehen. Oder gibt es da inzwischen ne einheitliche Definition?)
Im linken Fall ist es also so, dass alle Zustände in einem Band besetzt sind. Wenn wir einem Elektron ein klein wenig Energie zuführen, dann kann es mit dieser Energie nichts anfangen, weil es keinen Zustand gibt, in den es gehen könnte. Man kann deshalb die Elektronen nur mit sehr hohem Energieaufwand in andere Zustände bringen; Dinge wie schwache elektrische Felder reichen dafür nicht aus. Deshalb ist so ein Material ein Isolator: Elektronen können sich nicht bewegen, weil es keine passenden Zustände gibt, in die sie durch ein elektrisches Feld gehoben werden könnten.
Bei den Metallen sieht es ganz anders aus: Hier können wir auch mit geringer Energiezufuhr Elektronen in andere Zustände bringen, damit können sie sich frei bewegen und Strom und Wärme leiten. (Wie genau diese Zustände aussehen, gucken wir uns heute nicht an, das wäre relativ aufwändig.)
Mit dem Bändermodell in dieser einfachen Form können wir also schon einmal verstehen, warum es überhaupt Metalle und Isolatoren gibt – ohne Dinge wie Energieniveaus und das Pauli-Prinzip ginge das so nicht, auch hier bestimmt also die Quantenmechanik unseren Alltag.
Wärmeenergie
Also: Im Bändermodell sehen wir, dass wir Elektronen auch mit wenig Energie in andere Zustände bringen können – beispielsweise solche, bei denen sie Strom leiten. Das klappt aber nicht für alle Elektronen: Ein Elektron ganz unten im Band (bei sehr niedriger Energie) hat ja über sich erst mal jede Menge besetzte Zustände. Um dieses Elektron in einen anderen Zustand zu bringen, bräuchten wir also ziemlich viel Energie:
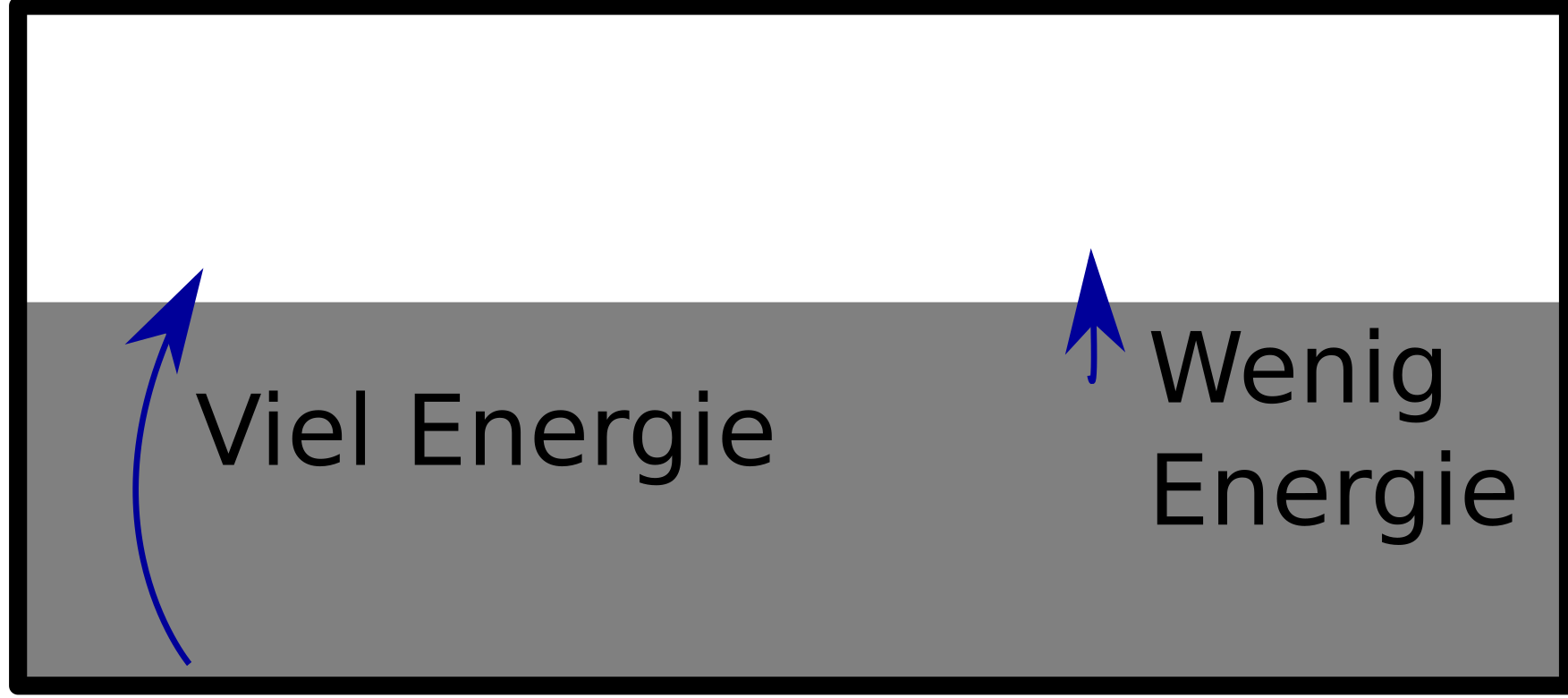
Wenig Energie brauchen wir dagegen, wenn ein Elektron schon eine relativ hohe Energie hat und knapp unterhalb der Grenze sitzt, die die besetzten von den unbesetzten Zuständen trennt. (Vornehm sagt man “Das Elektron sitzt an der Fermi-Kante”, weil diese Grenzenergie “Fermienergie” heißt, aber das müsst ihr euch nicht merken.)
Wenn wir unseren Löffel in das Heißgetränk stecken, dann wird Wärmeenergie auf die Elektronen übertragen. Wärmeenergie ist gewissermaßen “zufällig verteilte Energie”, je heißer es ist, desto größer ist die mittlere Energie, die man durch Wärme bekommt. Bei handelsüblichen Raum- oder Kaffee-Temperaturen ist diese Energie klein verglichen mit dem, was oben im Bild “viel Energie” heißt. Ein Elektron weit unten im Energieband kann also mit thermischer Energie nichts anfangen – die Eintrittskarte in den unbesetzten Bereich ist ziemlich teuer und ein paar Cent zu spendieren hilft da nicht.
Elektronen mit höherer Energie knapp unterhalb der Grenzenergie dagegen brauchen nur noch wenig zusätzliche Energie, um in einen unbesetzten Zustand zu kommen. Diese Elektronen können deshalb die thermische Energie aufnehmen (sie haben quasi schon 99,50€, und mit 50 cent können sie sich die 100€-Eintrittskarte leisten). Für die Wärmekapazität, also die Frage, wie viel thermische Energie unser Metall aufnehmen kann, sind nur diese Elektronen relevant.
Mit ein paar Formeln und ein bisschen Rechnerei kann man auch abschätzen, wie groß der Anteil der Elektronen ist, die Wärmeenergie aufnehmen können. (Das habe ich mit hinreichend viel Hinführung und Einzelschritten sogar mal als Klausuraufgabe in meiner Vorlesung rechnen lassen.) Und heraus kommt, dass etwa jedes 100te Elektron so dicht an der Grenze sitzt, dass es Wärmeenergie aufnehmen kann, also ist die Wärmekapazität nur ein Hundertstel so groß wie man nach der klassischen Theorie erwarten würde, wo alle Elektronen Wärme aufnehmen.
Elektrische Leitung und Wärmeleitung
“Aber Moment”, sagt jetzt die aufmerksame Leserin, “wenn das so ist, warum sind dann Metalle trotzdem gute elektrische Leiter? Denn dann können doch auch in einem elektrischen Feld nur sehr wenige Elektronen Energie aus dem Feld aufnehmen und in höhere Zustände kommen, wo sie Strom tragen? Also müssten Metalle doch nur mäßig gute Leiter sein?”
Gut gedacht. Um das zu verstehen, muss man sich die unterschiedlichen Zustände nochmal angucken, aber ich gehe hier nicht ins Detail (sonst kann ich gleich mein Buch abschreiben…). Elektronen kann man ja als Wellen beschreiben. (Details in meiner Schrödingergleichungs-Serie bei den Artikelserien.) Ein Elektron mit hoher Energie knapp unterhalb oder knapp oberhalb der Grenzenergie hat eine vergleichsweise kurze Wellenlänge. Zu einer kurzen Wellenlänge gehört aber eine hohe Geschwindigkeit (bzw. ein hoher Impuls, wenn ihr es physikalisch korrekter ausdrücken wollt [wenn es noch korrekter sein soll, müsste man vom Gitterimpuls reden…]). Diese Geschwindigkeit ist viel höher, als man es nach der klassischen Physik erwarten würde. Wenn wir also nur wenige Elektronen in leitende Zustände heben, dann haben diese wenigen Elektronen extrem hohe Geschwindigkeiten und können deshalb auch viel Strom transportieren. (Ein ganz analoges Problem habe ich mal in diesem Weihnachts-Artikel diskutiert.)
Wir haben also in der klassischen Physik sehr viele Elektronen, die alle Strom tragen, aber relativ langsam unterwegs sind. In der Quantenphysik dagegen tragen nur wenige Elektronen den Strom, die sind aber viel schneller (ungefähr hundert mal), und das kompensiert, dass es so wenige sind, die gesamte getragene Strommenge ist etwa dieselbe.
Die Überlegungen der klassischen Physik waren also sozusagen doppelt falsch: Die Zahl der Elektronen, die den Strom tragen, wurde um den Faktor 100 überschätzte, aber die Geschwindigkeit wurde um den Faktor 100 unterschätzt, und diese beiden Fehler kompensieren sich und führten dazu, dass das Drude-Modell sehr vernünftige Vorhersagen machen konnte.
Fazit
Auch wenn es auf den ersten Blick so aussieht, als könne man das Verhalten von Metallen mit der klassischen Physik verstehen – schaut man genauer hin, merkt man, dass nur die Quantenphysik tatsächlich korrekte Vorhersagen machen kann. Quanten sind eben überall.






Kommentare (43)