Es heißt ja oft, dass in unserem Alltag die klassische Physik gilt und dass Quanteneffekte normalerweise keine Rolle spielen. Für einige der besonders kniffligen Quantenphänomene wie beispielsweise die berühmte Quantenverschränkung ist das auch nicht ganz falsch, aber Quanteneffekte sind tatsächlich die Grundlage für alles, was wir im Alltag beobachten.
Nachdem wir schon gesehen haben, dass es letztlich Quanteneffekte sind, die verhindern, dass wir durch den Fußboden fallen, und dass wir die Eigenschaften von Metallen nur mit der Quantenmechanik (QM) erklären können, schauen wir heute auf einen anderen Alltagsgegenstand, den ihr alle besitzt (sonst könntet ihr diesen Text nicht lesen): Computer. (Einschließlich Handys, Tablets etc.)
Halbleiter
Computerchips sind deshalb so nützlich, weil sie Bauelemente enthalten, in denen man die elektrische Leitfähigkeit von Bauteilen auf ein Signal hin ändern kann. Man kann damit so genannte “Logische Gatter” basteln, beispielsweise ein UND-Gatter, bei dem die Ausgangsleitung (Y) nur dann ein Signal führt, wenn beide Eingangsleitungen (A und B) es tun:

Bild von Stefan506 CC BY-SA 3.0, Link
Nur wenn auf Leitung A und B ein Signal (eine logische 1) anliegt, gibt es auch bei Y ein Signal, sonst nicht. Genauso kann man ein ODER-Gatter bauen (Y ist eins wenn A oder B [oder beide] 1 sind), ein Nicht-Gatter (Hat nur eine Eingangsleitung, wenn eine 1 ankommt, kommt eine 0 raus und umgekehrt) usw.
All das funktioniert, weil Computerchips Halbleiter enthalten.
Halbleiter sind Materialien wie Silizium und Germanium. Im Periodensystem der Elemente (das man natürlich auch nur dank der QM verstehen kann, die ist wirklich überall, sollte ich vielleicht irgendwann nochmal erklären, auch wenn ich es in diesem Artikel schon ein bisschen getan habe) stehen sie unter dem Kohlenstoff. Sie haben 4 Elektronen auf der äußersten Elektronenschale, da ein Atom am liebsten 8 Elektronen dort hat, können sie Bindungen eingehen und so große Kristalle bilden, in denen jedes Atom mit 4 anderen verbunden ist. (Kohlenstoff kann das auch, aber die Bindung beim Kohlenstoff ist sehr stark, deswegen ist der kein Halbleiter.)
Silizium und Germanium sind deshalb auch keine Metalle (die geben ja Elektronen in ein “Elektronengas” ab), sondern Isolatoren. Im letzten Artikel über Metalle haben wir schon gesehen, dass es bei solchen Isolatoren eine energetische Lücke zwischen den besetzten und den unbesetzten Zuständen gibt:
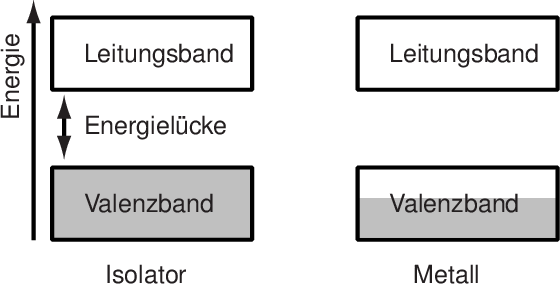
Bild aus meinem Buch “Funktionswerkstoffe”
Im sogenannten Valenzband sind aller Zustände mit Elektronen voll besetzt (jeder Zustand hat ja nur Platz für zwei Elektronen, das ist das berühmte Pauli-Prinzip der Quantenmechanik), dann gibt es einige Energiewerte, bei denen es keine Zustände gibt, dann folgt das sogenannte “Leitungsband”.
Wenn ein Elektron im Leitungsband ist, dann sind dort viele Zustände frei und unbesetzt, das Elektron kann deshalb seinen Zustand problemlos ändern und beispielsweise einen Zustand annehmen, in dem es sich in eine Richtung bewegt. Ein Elektron im Leitungsband kann also Strom tragen, wenn man ein elektrisches Feld anlegt. Aber in unserem Silizium (oder Germanium) scheint das ja wegen der Energielücke (oder Bandlücke) nicht zu gehen.
Wieso heißen diese Materialien dann Halbleiter, wenn sie doch anscheinend Nichtleiter (Isolatoren) sind?
Hier kommt jetzt – wie beim letzten Mal – die Wärmeenergie ins Spiel. Bei Temperatur Null, also ohne Wärmeenergie, sind alle Elektronen im Valenzband. Aber sobald wir die Temperatur erhöhen, können wir ja Elektronen Energie zuführen, denn Wärme ist ja eigentlich nichts anderes als Gratisenergie für irgendwelche atomaren Prozesse. (Oder physikalisch korrekter ausgedrückt: Wenn ihr ein System im Kontakt mit einem Wärmebad habt, dann gibt es eine Wahrscheinlichkeit dafür, dass ein atomarer Prozess, der Energie benötigt, diese Energie aus dem Wärmebad entnimmt. Details dazu findet ihr auch in meiner uralten Artikelserie zur Thermodynamik, klickt auf die Artikelserien-Liste.)
Allerdings ist die Energie, die man braucht, um ein Elektron über die Bandlücke zu heben, vergleichsweise groß gegen typische Energien. Es ist deshalb sehr unwahrscheinlich, ein Elektron in Silizium ins Leitungsband zu bekommen. Auf der anderen Seite hat Silizium aber auch ziemlich viele Elektronen (ein Kubikzentimeter Silizium hat etwa 50 000 000 000 000 000 000 000 oder kurz geschrieben 5e22 Atome). Zwar wird bei Raumtemperatur nur jedes Zehnbillionste Atom (eins von 10 000 000 000 000 oder 1:1e13) thermisch so stark angeregt, dass es sein Elektron ins Leitungsband schafft, aber das reicht, um eine gewisse Leitfähigkeit zu erreichen. Die ist zwar einige Größenordnungen kleiner als in Metallen, aber ein Isolator ist unser Halbleiter damit bei Raumtemperatur nicht mehr.
Löcherleitung
Wenn ein Elektron ins Leitungsband gehoben wird (soll also heißen, wenn ein Elektron so viel Energie bekommen hat, um über die Bandlücke zu kommen), dann ist der entsprechende Zustand, in dem das Elektron vorher war, jetzt ja unbesetzt. Im Valenzband fehlt also jetzt ein Elektron, es bleibt ein unbesetzter Zustand zurück, den man auch “Loch” nennt. Interessanterweise können auch Löcher Strom leiten.
Zu jedem der Zustände eines Elektrons gehört ja nicht nur eine Energie, sondern auch eine Geschwindigkeit. Im voll besetzten Valenzband gehört zu jedem Zustand, in dem ein Elektron nach rechts fliegt, einer, in dem das Elektron nach links fliegt, im Mittel hebt sich also alles auf.
Wenn aber beispielsweise ein Zustand unbesetzt ist, der zu einem Elektron gehört, das Geschwindigkeit Null hat, dann kann dieser Zustand von einem Elektron besetzt werden, das sich beispielsweise nach rechts bewegt hat. Damit haben wir jetzt in der Summe mehr Elektronen, die nach links fliegen (weil eins, das nach rechts geflogen ist, das jetzt nicht mehr tut), und damit haben wir jetzt auch einen Strom. Diese Art der Stromleitung nennt man “Löcherleitung”.
Das (halb-)klassische Modell
“Hey, hey, nicht so schnell”, mag jetzt der eine oder die andere sagen. “In der Schule hatte ich auch Halbleiter, und da haben wir das alles ohne viel Quantenmechanik erklärt.” Richtig. Man kann einige Aspekte von Halbleitern ganz gut mit folgendem einfachen Modell verstehen, das ich am besten mit einem Bild erkläre:
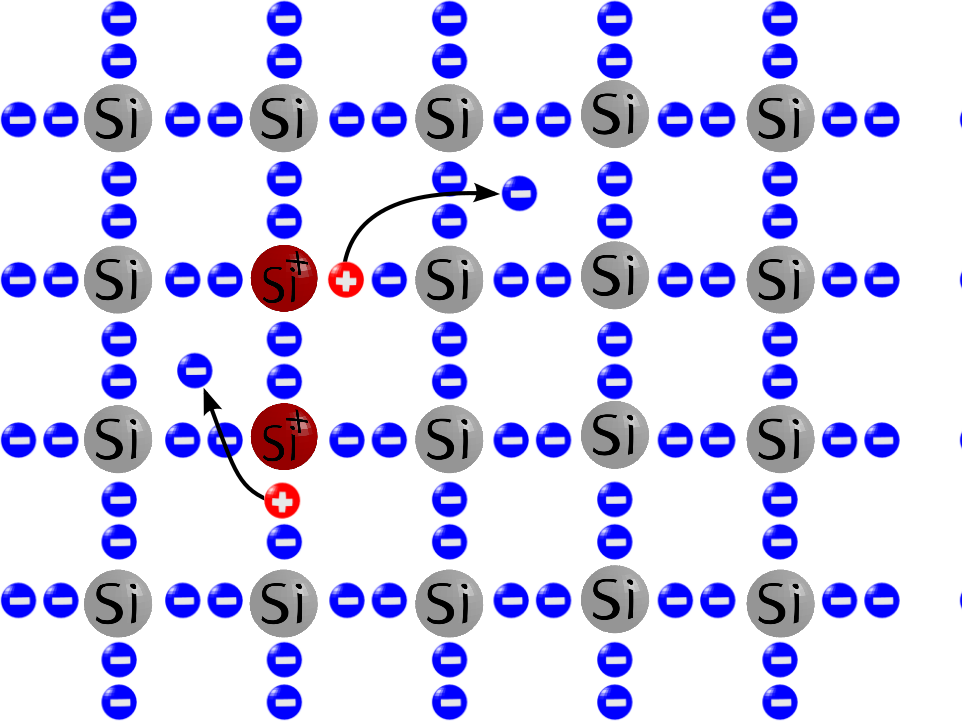
Bild aus meinem Buch “Funktionswerkstoffe”
Hier seht ihr einen schematisch (in zwei Dimensionen) gezeichneten Silizium-Kristall. Bei zwei der Si-Atome hat sich ein Elektron (durch die thermische Energie) aus der Bindung losgerissen, zurück bleibt ein positiv geladenes Si-Atom (also ein Ion), dem ein Elektron fehlt, bei dem also jetzt eine positive Ladung sitzt. Und in einem elektrischen Feld bewegen sich jetzt die Elektronen alle in eine Richtung, also kann die “Fehlstelle” sich in die andere Richtung bewegen:
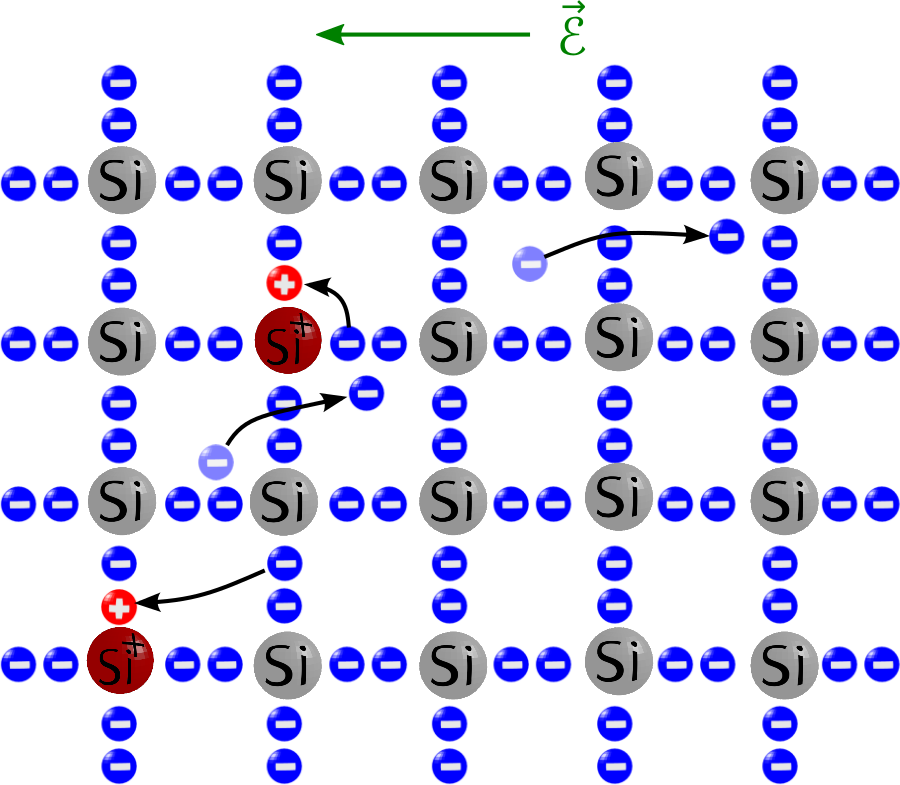
Bild aus meinem Buch “Funktionswerkstoffe”
Das Bild ist wirklich nicht schlecht und veranschaulicht das Verhalten von Elektronen und Löchern ganz gut. (Sonst würde ich es ja auch nicht in meiner Vorlesung zeigen.) Qualitativ gibt es einen guten Eindruck von dem, was passiert.
Aber die Quantenmechanik brauchen wir trotzdem. Zum einen natürlich schon deshalb, weil man ohne QM gar nicht verstehen könnte, wie die Bindung im Silizium überhaupt funktioniert. Zum anderen aber auch deshalb, weil das Verhalten von Elektronen und Löchern in Halbleitern etwas seltsam ist.
Beweglichkeit
Eine wichtige Größe in Halbleitern ist die sogenannte “Beweglichkeit”. Die gibt an, wie leicht sich die Ladungsträger (also Elektronen oder Löcher) bewegen können. Legt man ein elektrisches Feld an, werden die Elektronen (und Löcher) beschleunigt, bis der elektrische Widerstand eine weitere Beschleunigung verhindert. (Wie das im einzelnen funktioniert, erklärt man übrigens auch über die QM, das mache ich heute aber nicht…) Das Verhältnis aus Geschwindigkeit und Feldstärke ist dann die Beweglichkeit. Im einfachen Bild der Löcher bewegen sich Löcher ja, weil sich Elektronen bewegen. Man könnte also vermuten, dass die Beweglichkeit der Elektronen und Löcher gleich sein sollte, denn wenn sich Löcher bewegen, sind es ja letztlich auch Elektronen, die von einer Bindung zur nächsten hüpfen. Das ist aber nicht der Fall – die Beweglichkeit von Elektronen und Löchern kann stark unterschiedlich sein, in Si sind die Elektronen etwa 3-4mal beweglicher als die Löcher, im Halbleiter Indium-Antimonit aber etwa 60-mal. (Gut, man könnte versuchen zu argumentieren, dass es in einem Fall gebundene Elektronen sind, im anderen nicht. Qualitativ ist das o.k., aber Zahlen kann man so nicht vorhersagen.)
Die QM kann diese Effekte auch quantitativ erklären, weil sie die Wechselwirkung der Elektronen (oder Löcher) mit dem Kristallgitter beschreiben kann. Dazu muss man sich die Zustände der Elektronen etwas genauer angucken. Bisher haben wir ja das Bändermodell einfach nur mit Energien dargestellt, so wie im Bild oben, aber wenn man genau verstehen will, was die Elektronen im Kristall tun, muss man zusätzlich auch ihren Wellencharakter anschauen.
Elektronen lassen sich in der QM ja als Wellen darstellen. Bei freien Elektronen (die also nicht an irgendwelche Atome oder so gebunden sind) ist die Energie um so größer, je kleiner die Wellenlänge dieser Welle ist. Meist verwendet man zum Schreiben dieser Beziehung nicht die Wellenlänge, sondern die sogenannte “Wellenzahl” k, die ist im Wesentlichen der Kehrwert der Wellenlänge. Für freie Elektronen gilt einfach, dass E proportional zum Quadrat der Wellenzahl ist (E~k²). Malt man die Beziehung zwischen E und k auf, ergibt sich also eine Parabel:
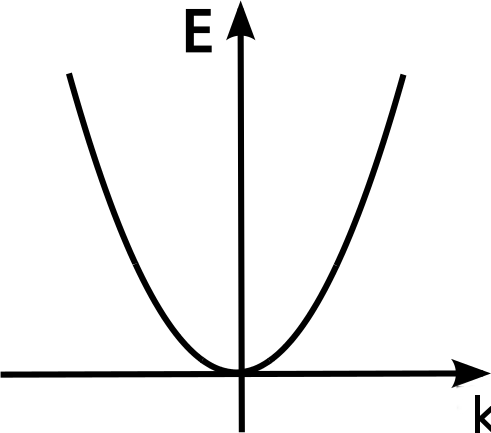
Wenn sich die Elektronen aber in einem Kristallgitter tummeln, so wie sie das im Silizium tun, dann sieht das entsprechende Bild (Bänderdiagramm genannt) deutlich komplizierter aus:
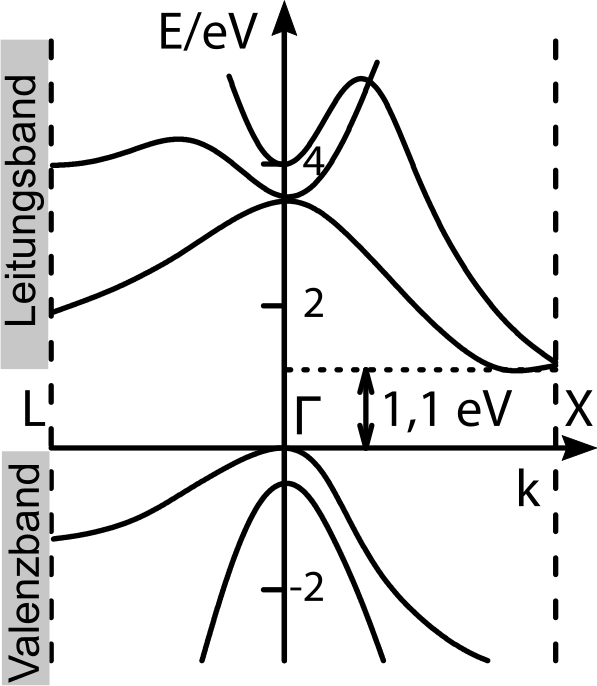
Bild aus meinem Buch “Funktionswerkstoffe”
Dieses Bild zeigt das Bänderdiagramm von Silizium; ihr seht schon, dass es etwas komplizierter ist als die einfache Parabel. (Ein Teil der Komplexität kommt dadurch, dass ich den dreidimensionalen Charakter der Wellen im Bild mit eingebaut habe, aber Dinge wie die Bandlücke stammen direkt von der Wechselwirkung mit dem Kristallgitter.) Links seht ihr schematisch das Valenz- und Leitungsband eingezeichnet, die Linien zeigen, zu welchem Wert der Wellenzahl welche Energie gehört. (Auf Kürzel wie L, Gamma und X gehe ich hier nicht ein.)
Aus solchen Diagrammen kann man jetzt direkt Rückschlüsse auf die Beweglichkeit der Elektronen und Löcher ziehen, und ohne die QM (mit dem daraus folgenden Wellencharakter der Elektronen) wäre das nicht möglich.
Warnhinweis: Die Wellenzahl k wird auch gern als Impuls (oder korrekter “Gitterimpuls”) bezeichnet. Das ist auch physikalische korrekt, man darf aber nicht die handelsübliche Beziehung Impuls gleich Masse mal Geschwindigkeit verwenden und annehmen, dass Impuls und Geschwindigkeit proportional sind. Sind sie im Kristallgitter nicht, es kann sein, dass ein Elektron negativen Impuls aber positive Geschwindigkeit hat, weil man die Geschwindigkeit der Elektronen physikalisch sinnvoll über die Gruppengeschwindigkeit eines Wellenpakets ausdrücken sollte. Das erkläre ich jetzt aber nicht; selbst in meinem Buch habe ich das in einen Abschnitt für die Fortgeschrittenen verbannt, ich sage es nur, weil man jede Menge Blödsinn herausbekommen kann, wenn man einfach p=mv annimmt…
Zahl der Ladungsträger
Wichtig für Halbleiter-Bauteile wie die Chips in eurem Computer ist auch die Zahl der Ladungsträger. (Die wird allerdings durch sogenanntes Dotieren, also das gezielte Hinzufügen anderer chemischer Elemente, verändert; die Zahl der Ladungsträger in reinem Si ist aber trotzdem eine extrem wichtige Design-Variable, die sogenannte “intrinsische Ladungsträgerdichte”).
Man könnte naiv annehmen, dass man mit dem einfachen Bänderdiagramm, das ich oben gezeichnet habe, leicht herausbekommen kann, wie viele Elektronen im Leitungsband (und entsprechend Löcher im Valenzband) sind: Wir kennen die Größe der Bandlücke, wir wissen aus der Thermodynamik, wie groß die Wahrscheinlichkeit ist, dass ein Elektron durch thermische Anregung die entsprechende Energie bekommt, wir wissen, wie viele Elektronen wir haben, also sollten wir leicht ausrechnen können, wie groß die Zahl der Elektronen im Leitungsband ist.
Ganz so einfach ist es aber nicht, denn es sind ja nicht alle Elektronen in einem Zustand direkt an der Bandlücke, und die Elektronen haben ja auch unterschiedliche Zustände, in die sie im Leitungsband gehen können. Nach den Regeln der statistischen Physik müssen wir berücksichtigen, wie viele Elektronen wie dicht an der Bandlücke sind und wie viele Zustände oberhalb der Bandlücke es gibt. Genau diese Information kann man aus dem Diagramm oben ablesen: Da, wo eins der Bänder flach verläuft, gibt es viele Zustände mit nahezu derselben Energie; da wo eins der Bänder steil ist, ändert sich die Energie stark , wenn man die Wellenzahl auch nur ein wenig ändert. Mit dieser Logik (und ein bisschen Mathematik) kann man aus dem Bänderdiagramm die benötigte Information herauskitzeln, wie viele Zustände mit welcher Energie es gibt (die sogenannte Zustandsdichte), und mit der lässt sich dann tatsächlich ausrechnen (und aus dem Bänderdiagramm vorhersagen), wie viele Elektronen ich bei welcher Temperatur im Leitungsband finde.
Fazit
Mit einfachen Mitteln, beispielsweise dem Bild, das ich oben gezeigt habe und das ihr vielleicht aus dem Physikunterricht kennt, kann man qualitativ ganz gut verstehen, was in Halbleitern passiert. Aber um Bauteile aus Halbleitern zu bauen, reicht das nicht, dazu muss man die Eigenschaften wie beispielsweise die Beziehung zwischen Energie und Wellenlänge, auch quantitativ verstehen. Und das ist ohne Quantenmechanik nicht möglich. Jedes Mal, wenn ihr euer Handy einschaltet und es wie erwartet funktioniert, habt ihr damit letztlich ein Experiment zur Bestätigung der Quantenmechanik gemacht.
PS: Ich habe jetzt nicht erklärt, wie man mit Halbleitern so ein logisches Gatter bauen kann, das wäre ein eigener Blog-Artikel. Interessiert das irgendwen?






Kommentare (11)