Im Jahr 1766 glaubte der Astronom Johann Daniel Titius von der Universität Wittenberg, er hätte eine gewisse Regelmäßigkeit im Aufbau des Sonnensystems entdeckt. Die Planeten wären nicht einfach willkürlich um die Sonne verteilt, sondern folgten mit ihrem Abständen einem mathematischen Gesetz. Ein Gesetz, das wir heute als die “Titius-Bode-Reihe” kennen und dessen Geschichte ich hier in aller Ausführlichkeit beschrieben habe. Die Titius-Bode-Reihe hat in der Geschichte der Astronomie eine wichtige Rolle gespielt. Denn zur Zeit von Titius hatte sie eine Lücke. Sein Gesetz funktionierte nur, wenn man davon ausging, dass sich zwischen Mars und Jupiter noch ein Planet befindet. Und weil man Ende des 18. Jahrhunderts wirklich fest davon überzeugt war, dass die Titius-Bode-Reihe korrekt ist, machte man sich auf die Suche nach diesem fehlenden Planeten. Im Jahr 1801 wurde man tatsächlich fündig; man entdeckte zuerst den Asteroid Ceres und danach noch Dutzende andere kleine Himmelskörper an der von Titius vorhergesagten Stelle. Gut, es war kein Planet, aber trotzdem hatte man dank der Titius-Bode-Reihe ein paar neue Himmelskörper entdeckt! Vielleicht klappt das ja auch in extrasolaren Planetensystemen?
Im 19. Jahrhundert zeigte sich mit der Entdeckungen von Neptun dass die Reihe nicht mehr stimmt. Dieser Planet sollte eigentlich laut der Titius-Bode-Reihe gar nicht existieren. Mittlerweile ist man größtenteils der Meinung, dass die Abstandsregel von Titius nur eine mathematische Spielerei ohne echten physikalischen Hintergrund ist. Sie hatte nur “funktioniert”, weil Titius die Parameter passend hingebogen und die diversen Ungenauigkeiten ignoriert hatte.
Aber trotzdem gibt es immer wieder Wissenschaftler, die sich Gedanken darüber machen, ob die Abstände der Planeten vielleicht doch irgendeiner Regel folgen und vorhergesagt werden können. Das wäre besonders praktisch, wenn es um extrasolare Planeten geht. Hier ist unser Wissen aus technischen Gründen meist beschränkt und wir kennen selten alle Planeten, die einen fremden Stern umkreisen sondern immer nur ein paar. Wenn man aus den Abständen dieser paar bekannten Planeten vorhersagen könnte, wo sich andere Planeten befinden, dann wäre das eine ziemlich großartige Sache! Und genau das ist es, was Timothy Bovaird und Charles H. Lineweaver von der Australian National University in Canberra in ihrem Artikel “Exoplanet Predictions Based on the Generalised Titius-Bode Relation” probieren.
Bovaird und Lineweaver verwenden natürlich nicht die originale Titius-Bode-Reihe aus dem 18. Jahrhundert sondern eine verallgemeinerte Version. So sieht sie aus:
an ist die große Halbachse des n-ten Planeten, also der mittlere Abstand des Planeten zum Stern. n ist die Nummer des Planeten; bei uns im Sonnensystem hätte zum Beispiel Merkur die Nummer 0, Venus hätte n=1; die Erde n=2; der Mars n=3; und so weiter. a (nicht mit an verwechseln – die Parameter wurden hier etwas unglücklich benannt!) und C sind zwei Zahlen, die für jedes Planetensystem die Abstände bestimmen und genau die Parameter, die man herausfinden muss. Kennt man a und C dann kann man ganz einfach berechnen, wo sich Planeten befinden müssen.
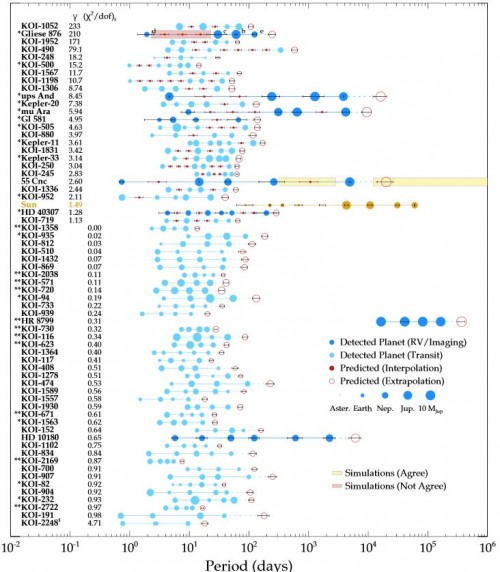
Bovaird und Lineweaver haben sich nun alle extrasolaren Planetensysteme angesehen, bei denen man mindestens 4 Planeten kennt. Dort haben sie probiert, a und C so zu bestimmen, dass die Beobachtungsdaten damit am besten beschrieben werden. Anschließend haben sie nachgesehen, ob die so definierten allgemeinen Titius-Bode-Reihen die Existenz noch unbekannter Planeten vorhersagen. Hier ist eine Übersicht über die Ergebnisse.
Von oben nach unten sind die verschiedenen Planetensysteme aufgeführt (Wichtig: Die meisten diese Planeten sind nur Planetenkandidaten und wurden noch nicht bestätigt!). Die Zahlen neben den Namen sind ein Maß dafür, wie gut sich das System mit einer Titius-Bode-Reihe beschreiben lässt. Die Abstände der Planeten von ihrem Stern sind hier durch die Umlaufzeit angegeben (Je geringer der Abstand desto geringer ist nach dem dritten Keplerschen Gesetz auch die Umlaufzeit). Blaue Kreise symbolisieren bekannte Planeten (hellblau sind die, die mit der Transitmethode entdeckt wurden; dunkelblau die anderen). Die roten bzw. rot gefüllten Kreise geben an, wo die Titius-Bode-Reihen noch unbekannte Planeten vorhersagen und die Größe aller Kreise symbolisiert die Masse der Planeten.

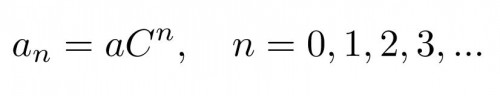










Kommentare (17)