In meiner Serie “Best of Chaos” komme nun endlich die Fraktale an die Reihe. Fraktale sind wirklich seltsam. Sie sind da, aber auch nicht. Sie sind unendlich groß, aber auch nicht. Sie scheinen völlig unnatürlich und haben sich trotzdem als hervorragender Weg herausgestellt, die Natur zu beschreiben. Eigentlich besteht die Chaostheorie ja aus jeder Menge heftiger Mathematik – siehe dazu meine früheren Blogartikel (Einleitung, Teil 1, Teil 2, Teil 3, Teil 4) und meine Podcasts (Folge 93). Diese komplexe Mathematik ist auch nötig, wenn man es mit so seltsamen Objekten wie den Fraktalen zu tun hat…
Ich habe bisher schon vom “seltsamen Attraktor” gesprochen. Außerdem von der Verdoppelung der Perioden in chaotischen Systemen, der Universalität des Chaos und die Mandelbrot-Menge. Die letzte Folge über die Mandelbrotmenge hat schon gezeigt, das wir eine völlig neue Geometrie brauchen, um das Chaos zu beschreiben. Und die Fraktale zeigen uns, wie das aussehen könnte.
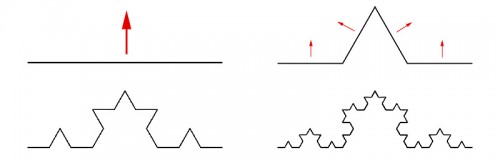
Ein Fraktal ist ein bestimmtes geometrisches Gebilde oder Muster, das sich nicht mit dem normalen Dimensionsbegriff beschreiben lässt. Normalerweise sind Dinge entweder eindimensional (zum Beispiel eine Linie), zweidimensional (eine Fläche) oder dreidimensional (ein ausgedehnter Körper) – und ein Punkt ist nulldimensional. Ein Fraktal passt in dieses Schema aber nicht hinein. Ein klassisches Beispiel dafür ist die Koch-Kurve oder “Schneeflocken-Kurve”. Sie fängt ganz harmlos an, in dem man einfach eine gerade Linie zeichnet. Diese Linie teilt man in drei gleich große Teile und ersetzt den mittleren Teil durch ein gleichseitiges Dreieck (kein komplettes, die untere Linie des Dreiecks lässt man weg). Jede der beiden jetzt aus der Linie aufragenden Dreieckseiten teilt man wieder in drei Teile und wiederholt den Prozess. Und dann nochmal. Das sieht dann so aus:
Aber warum sollte man jetzt schon damit aufhören? Man kann das Spiel immer weiter treiben und immer mehr Dreiecke aneinander reihen. Unendlich viele sogar. Logischerweise muss diese Kurve dann irgendwann auch unendlich lang werden – wenn ich unendlich oft eine gerade Linie durch eine etwas längere dreieckige Linie ersetze, ist das unausweichlich. Die Länge der Koch-Kurve ist also unendlich groß. Aber trotzdem kann die Fläche unter der Koch-Kurve NICHT unendlich groß sein. Auch das sieht man leicht: Die hinzugefügten Dreiecke werden mit jedem Schritt immer kleiner und wenn ich um die ursprüngliche Kurve einen Kreis ziehe, wird auch die unendlich lange Kurve nie darüber hinaus reichen. Man kann mathematisch relativ einfach ausrechnen, wie groß der Flächeninhalt nach unendlich vielen Schritten sein muss und er erreicht nie einen unendlich großen Wert.
Eine unendlich lange Kurve umschließt also eine endlich große Fläche… Es ist klar, dass man hier mit normaler Geometrie nicht weiter kommt. Die Dimension der Koch-Kurve wird daher auch nicht mit den klassischen Werte von “1”, “2” oder “3” beschrieben. Die sogenannte “fraktale Dimension” der Koch-Kurve beträgt ca. 1,26 (exakt: log(4)/log(3)). Man kann sich das in etwa so vorstellen: Eigentlich wäre die Koch-Kurve ja nur eine normale Linie mit der Dimension 1. Aber weil sie sich so sehr in sich selbst verschachtelt, ist sie mehr als nur eine Linie. Sie ist zwar noch keine komplette zweidimensionale Fläche, hat aber wegen ihrer unendlichen Länge und der verschachtelten Form schon ein bisschen “flächenhafte” Eigenschaften und daher eine Dimension, die zwischen 1 und 2 liegt. Wenn man drei solcher Koch-Kurven aneinander fügt, bekommt man die berühmte Schneeflocke (die man dann natürlich auch noch schön bunt einfärben kann):
Ist das jetzt nur eine mathematische Spielerei? Nicht wirklich – bei der Betrachtung der Natur stößt man schnell auf ähnlich fraktale Phänomene. Das klassische Beispiel dafür ist die Frage nach der Länge einer Küstenlinie. Wie lang zum Beispiel ist die Linie, die einmal um die britische Hauptinsel herum führt? Man kann das natürlich einfach mit einem Atlas und einem Lineal ausmessen und wird dann einen bestimmten Wert bekommen. Aber in einem normalen Atlas sind viele kleine Buchten nicht eingezeichnet. In einer detaillierten Karte wird man eine viel verschachteltere Küstenlinie finden, die beim Ausmessen dann auch länger ist. Und im Prinzip könnte ich mir auch einen Maßstab nehmen, der einen Meter lang ist und damit einmal um die ganze Insel wandern und alles per Hand ausmessen. Oder ich nehme einen Maßstab, der nur einen Zentimeter lang ist – dann wird alles noch genauer. Und noch länger. Denkt man dieses Prozess zu Ende, dann kommt man darauf, dass die Küste unendlich lang ist. Natürlich wird man irgendwann aufhören müssen zu messen, wenn man bei einzelnen Atomen angekommen ist, aber das Prinzip ist das selbe wie bei der Koch-Kurve (weswegen man auch in vielen Nachschlagewerken deutlich unterschiedliche Werte für die Länge vieler Grenzen findet).
Was die Fraktale in der Natur so populär macht, ist auch ihre Selbstähnlichkeit. Ein vergrößerter Teil der Koch-Kurve sieht wie die Koch-Kurve selbst aus. Man braucht nur eine simple Konstruktionsregel anzugeben, um am Ende große und sehr komplexe Strukturen zu erhalten. Ein wunderschönes Beispiel für fraktale Geometrie in der Natur ist der (weniger wunderschön schmeckende) Romanesco:
Aber auch viele Farne zeigen fraktale Strukturen. Und Blitze. So wie die Ränder von Wolken. Und die Verästelungen der Blutgefäße im menschlichen Körper. Oder wachsende Kristalle bzw. sich vermischende Flüssigkeiten. Und manchmal baut man sogar welche, zum Beispiel um Funksignale besser zu empfangen. Bei der Beschreibung der Natur bzw. von dynamischen Prozessen sind fraktale Dimensionen mittlerweile ein wichtiges Hilfsmittel (ich habe sogar meine Diplomarbeit über dieses Thema geschrieben). In der Natur sind die Dinge natürlich nie so exakt wie in der mathematischen Beschreibung der Fraktale (wer mehr dazu wissen will, soll diesen Blogartikel lesen). Aber man kann damit viel Nützliches anstellen. Und abgesehen davon schauen sie auch meistens enorm hübsch und faszinierend aus!













Kommentare (23)