Es gibt einen (amerikanischen) Werbespot eines Vitaminpillen-Herstellers, in dem behauptet wird, das menschliche Auge könne die Flamme einer Kerze noch in 16 Kilometer Entfernung sehen (hier könnt ihr den Spot sehen). Stimmt das? 16 Kilometer ist ja jetzt nicht so enorm weit – und wenn es wirklich dunkel ist, könnte das nicht vielleicht doch klappen? Mir kam dieser Wert jedenfalls trotzdem ein bisschen hoch vor. Die Lichter von Städten vielleicht; die Lichter eines Fussballstadiums, ein hell beleuchtetes Schiff auf dem Ozean: Das würde ich noch akzeptieren. Aber so eine Kerze ist nicht unbedingt hell.
Aber zum Glück gibt es Astronomen! Und wenn Astronomen etwas wirklich gut können, dann ist es herauszufinden, wie hell irgendwo etwas leuchtet und diese Helligkeit zu messen. Deshalb haben sich Kevin Krisciunas und Don Carona von der Texas A&M University, angeregt durch oben erwähnten Werbespot, entschieden, das ganze einfach mal zu testen! Ihre Ergebnisse haben sie kürzlich veröffentlicht (“At What Distance Can the Human Eye Detect a Candle Flame?”).
Der Versuchsaufbau war einfach: Mit einer CCD-Kamera haben sie zuerst den Stern Wega vermessen. Der ist auf jeden Fall mit freiem Auge zu sehen und das, obwohl er ganze 25 Lichtjahre weit entfernt ist. Aber Wega ist ja auch keine Kerze, sondern ein großer und heißer Stern mit der 37fachen Leuchtkraft unserer Sonne. Deswegen gehört er auch zu den hellsten Sternen, die man am Himmel sehen kann und weil er noch dazu auf der Nordhalbkugel in jeder Nacht am Himmel zu sehen ist und seine Helligkeit ziemlich genau einer Größenklasse von 0 Magnituden entspricht, wurde er früher oft als Referenzpunkt für Helligkeitsmessungen verwendet (Die Sache mit den Helligkeiten von Sternen und Magnituden habe ich hier ausführlich erklärt).
An Wega haben die beiden Astronomen also ihre Kamera kalibriert und dann mit dem gleichen Gerät eine Kerze in 338 Metern Entfernung beobachtet. Nach der Auswertung aller Daten kamen zu dem Schluss, dass die Kerze 2,423 Größenklasse heller als Wega leuchtet. Man muss aber bei den astronomischen Helligkeiten aufpassen. Wenn von “Größenklassen” oder “Magnituden” die Rede ist, darf man nicht vergessen, dass größere Werte hier einer geringeren Helligkeit entsprechen! Helle Sterne haben also zum Beispiel eine Helligkeit von 0 oder 1 Magnitude während schwach sichtbare Sterne zur 5. oder 6. Größenklasse gehören. Zweitens ist die Magnitude/Größenklasse ein Wert der angibt, wie hell uns ein Himmelskörper erscheint, aber keine Beschreibung der tatsächlichen Lichtmenge die uns von dem Stern erreicht. Das ist der Fluss und der Zusammenhang zwischen Magnitude und Fluss ist nicht linear, sondern logarithmisch.
Wenn also der Unterschied zwischen Kerze und Wega 2,423 Magnituden beträgt, kommt von ihr 9,315 mal mehr Licht an als vom Stern. Das alles sagt uns aber noch nichts über die Frage, bis zu welcher Entfernung eine Kerze noch sichtbar ist. Aber die Messungen und den Vergleich mit Wega kann man nutzen, um das zu berechnen.
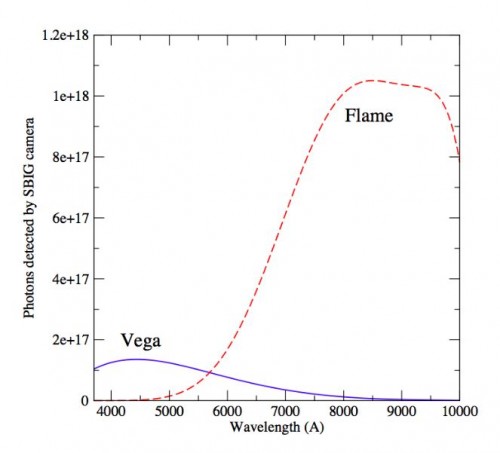
Gemessene Photonen von Wega und Kerze, in Abhängigkeit der Wellenlänge (Bild: Krisciunas & Carona, 2015)
Dafür muss man die Temperatur berücksichtigen, die natürlich bei Wega (ein heißer Stern mit einer Oberflächentemperatur von bis zu 10.000 Grad) natürlich viel größer ist als bei einer Kerze. Man muss die Empfindlichkeit der Kamera und des Auges berücksichtigen und die Tatsache, dass man bei Tag mehr Farben d.h. unterschiedliche Wellenlängebereiche sehen kann als in der Nacht. Und man muss einen durchschnittlichen Wert für die Helligkeit definieren, bei der etwas für das Auge gerade noch sichtbar ist. Das ist natürlich von Mensch zu Mensch unterschiedlich (und hängt von den äußeren Bedingungen ab). Normalerweise gilt aber ein Wert von 6 Größenklasse als Grenze: Alles was schwächer leuchtet, kann vom freiem Auge nicht mehr gesehen werden.












Kommentare (40)