Bei der Bewegung von Himmelskörpern geht nichts über die Gravitation. Die gravitative Anziehungskraft zwischen Galaxien, Sternen, Planeten, Asteroiden, etc bestimmt wie sich diese Objekte bewegen. Andere Kräfte kann man so gut wie immer ignorieren. Aber eben nur so gut wie immer. Will man zum Beispiel wissen, wo der Planet Mars in zwei Tagen, zwei Wochen oder zwei Jahrzehnten am Himmel zu sehen ist, dann kriegt man das problemlos und rein unter Berücksichtigung der Gravitationskräfte von Sonne und den anderen Planeten hin. Will man dagegen wissen, wohin sich ein kleiner Asteroid in den nächsten paar Jahren bewegt und will man das wirklich, wirklich genau wissen, dann reicht die Gravitationskraft nicht aus. Dann muss man auch die winzigen Effekte berücksichtigen die von anderen Kräften verursacht werden. Zum Beispiel den Jarkowski-Effekt.

Wenn Asteroiden vom Weg abkommen kann das richtig ärgerlich sein… (Standardbild zur Illustration von Asteroideneinschlägen: NASA/JPL)
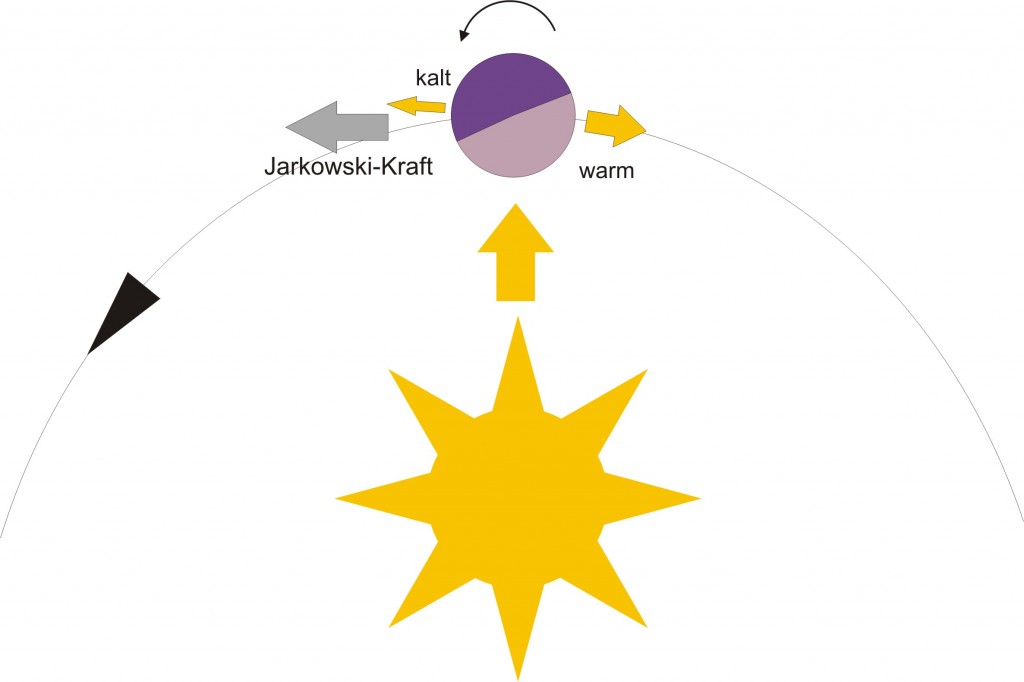
Was das ist habe ich früher schon mal sehr ausführlich erklärt. Kurz gesagt: Ein Asteroid wird durch die Strahlung der Sonne aufgewärmt. Natürlich nur auf der Seite die gerade in Richtung Sonne zeigt. Die ändert sich aber ständig weil so ein Asteroid ja um seine Achse rotiert. Die aufgewärmten Stellen geben die Wärme wieder ins All ab und zwar um so besser je wärmer sie sind. Diese Abstrahlung kann man sich wie einen kleinen “Rückstoß” vorstellen und weil sich der Asteroid dreht und unterschiedliche Stellen unterschiedlich stark aufgeheizt werden und unterschiedlich stark Wärme abgeben, verteilt sich der Rückstoß nicht gleichmäßig. Es gibt eine winzige resultierende Kraft die dafür sorgt dass die Bewegung des Asteroiden sich minimal von der Bewegung unterscheidet die allein von der gravitativen Beeinflussung durch Sonne und die anderen Planeten zu erwarten ist.
Das ist der Jarkowski-Effekt und er spielt wirklich nur bei kleinen Himmelskörpern eine Rolle. Ab einer gewissen Größe verteilt sich die Aufwärmung und Abkühlung so sehr, dass die resultierende Kraft verschwindend gering wird. Aber bei den Asteroiden muss man ihn eben berücksichtigen wenn man wirklich genau wissen will, wie sich der Felsbrocken bewegt. Die Bahn des Asteroid Golevka zum Beispiel (einer der ersten Himmelskörper bei dem man diesen Effekt gemessen hat) wurde zwischen 1991 und 2003 sehr genau vermessen und am Ende zeigte sich das er 3,7 Meter entfernt von der Position war an der er sich eigentlich befinden hätte sollen wenn man nur die Gravitation berücksichtigt.
3,7 Meter sind nicht viel und kein Problem wenn man zum Beispiel einfach nur wissen will wo am Himmel das Ding ist weil man sein Teleskop darauf richten will. Aber selbst so eine kleine Abweichung kann relevant sein wenn es etwa um die Frage geht ob ein Asteroid irgendwann mit der Erde kollidiert oder nicht. Da müssen die Rechnungen wirklich genau sein; da kommt es auf jeden Meter an. Und deswegen auch auf den Jarkowski-Effekt.
Und netterweise haben kürzlich Adam Greenberg von der University California und seine Kollegen unser Wissen über den Jarkowski-Effekt bei erdnahen Asteroiden deutlich erweitert (“Yarkovsky Drift Detections for 159 Near-Earth Asteroids”). Sie haben Beobachtungsdaten aller bekannten erdnahen Asteroiden genommen und mit der vorhergesagten Bewegung verglichen die diese Objekte unter dem gravitativen Einfluss der Sonne, der acht Planeten und 24 der massereichsten Asteroiden ausführen müssten. Bei 159 Asteroiden haben sie kleine Abweichungen von dieser rein durch die Gravitationskraft vorhergesagten Bahn gefunden. Abweichungen die auf den Jarkowski-Effekt zurück zu führen sind.
Die Abweichungen sind, wie schon gesagt, sehr klein. Die “Driftraten” die Greenberg und seine Kollegen bestimmen konnten lagen typischerweise im Bereich von 10.000 Kilometer während einer Million Jahre. Aber wo man vorher nur bei ein paar Dutzend Asteroiden den Jarkowski-Effekt nachweisen konnte, sind es durch die besseren Beobachtungen und die besseren Berechnungsmethoden nun eben schon über 150. Diese Menge an Daten hat es den Astronomen auch erlaubt den Zusammenhang zwischen der Größe der Asteroiden und der Stärke des Effekts zu überprüfen. Aus der theoretischen Berechnung der Aufwärmung und Abkühlung folgt, dass der Effekt indirekt proportional zum Durchmesser des Asteroiden ist: Je größer der Asteroid desto geringer der Effekt. Und genau das zeigen nun auch die realen Beobachtungsdaten.
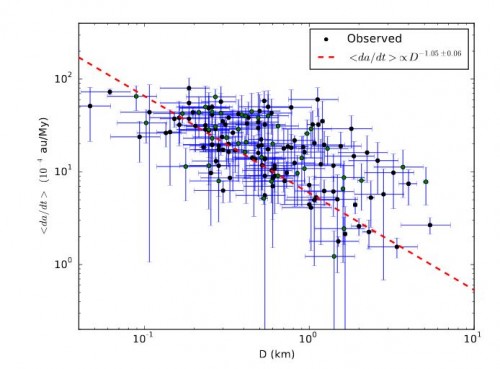
Zusammenhang zwischen Driftrate und Asteroidendurchmesser (Bild: Greenberg et al, 2017)
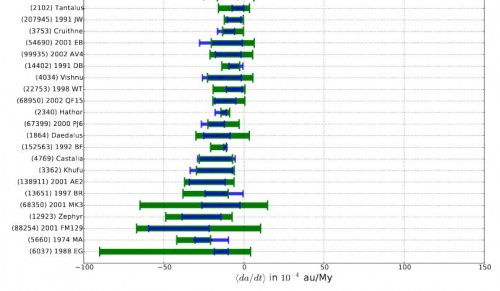
Zusätzlich bietet der Jarkowski-Effekt eine Möglichkeit mehr über die Rotation von Asteroiden herauszufinden. Die können sich ja entweder “prograd” um ihre Achse drehen oder “retrograd”. Im ersten Fall drehen sie sich in die gleiche Richtung in der sie sich auch um die Sonne bewegen; im zweiten Fall ist es umgekehrt. Die Rotationsrichtung lässt sich aus der Ferne allerdings nur schwer bis gar nicht beobachten. Sie hat aber einen Einfluss auf den Jarkowski-Effekt: Bei prograd rotierenden Asteroiden führt er i.A. dazu das die Driftrate positiv ist; der Asteroid seine Bahn im Laufe der Zeit also vergrößert. Bei den retrograden Asteroiden verkleinert sich die Bahn dagegen normalerweise durch den Jarkwoski-Effekt. Das Verhältnis von negativer zu positiver Driftrate liefert also Hinweise auf das Verhältnis von retrograd zu prograd rotierenden Asteroiden und liegt bei der Untersuchung von Greenberg und seinen Kollegen bei etwa zwei. Es scheinen also doppelt so viele der untersuchten Asteroiden retrograd zu rotieren wie prograd.
In Zukunft wird man aus der Untersuchung des Jarkowski-Effekts noch viel mehr lernen können. Je größer die Datenbank wird, desto besser können wir die Vergangenheit der Asteroiden nachvollziehen. Wir können verstehen wie sich Asteroidenfamilien gebildet haben nachdem größere Objekte auseinandergebrochen sind und sich die Bahnen der Bruchstücke im Laufe der Zeit voneinander entfernt haben. Wir werden viel über die unterschiedliche Zusammensetzung der Asteroiden lernen. Und wir werden auch mehr über ihre zukünftige Entwicklung wissen. Die Bahnen von erdnahen Asteroiden werden wir noch genauer vorhersagen können als es jetzt der Fall ist und damit auch noch besser wissen, ob irgendwann einer davon vielleicht mit der Erde kollidieren könnte oder nicht (Kurzer Hinweis: Der Asteroid 2012 TC4 der am 12. Oktober 2017 in der Nähe der Erde vorbei fliegen wird, stellt keine Gefahr da. Auch wenn die üblichen Panikmedien das wahrscheinlich wieder anders erzählen werden).
Die Gravitationskraft dominiert die großräumigen Entwicklungen im Universum. Aber manchmal muss man eben auch auf die Details achten. Selbst wenn es nur um aufgewärmte Felsbrocken im All geht…











Kommentare (14)