Wir basteln uns einen Elektronenspin

Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2017. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details dazu gibt es hier. Eine Übersicht über alle am Bewerb teilnehmenden Artikel gibt es hier. Informationen zu den Autoren der Wettbewerbsartikel finden sich in den jeweiligen Texten.
——————————————————————————————————————

Wir basteln uns einen Elektronenspin

von Wolfram Nitsch

Dieser Text (mein erster Blogtext überhaupt) wendet sich an jene Physik-interessierten Laien unter euch, die gerne mal einen Mathematik-freien* Blick hinter die Kulissen der Quantenmechanik werfen würden. In dem folgenden Text findet ihr dazu ein simples Gedankenmodell, welches das Elektron, seinen Spin und die Messung dieses Spins modelliert.

Mit diesem Gedankenmodell führen wir dann einige spezifische Gedankenexperimente durch und lernen so extrem einfache Beispiele für die quantenmechanischen Charakteristiken des Spins kennen, beispielsweise den deterministischen Spin-Zustand und die indeterministische Spin-Messung, die Quantisierung des Spins, die Präparation und Zerstörung eines Spin-Zustandes, die Wiederholbarkeit und Unschärfe einer Spin-Messung, die Spin-Phase und die phaseninvariante Spin-Messung und noch andere Köstlichkeiten.
(*) Ok, Sinus und Kosinus laufen euch an einer Stelle über den Weg, die könnt ihr aber getrost ignorieren weil die dazugehörigen Diagramme direkt daneben stehen. 😉

1. Der seltsame Elektronenspin

Wenn Physiker versuchen den Spin des Elektrons einem Laien zu erklären, dann verwenden sie dafür gerne die Modellvorstellung einer geladenen und rotierenden Elektronenkugel, die Rotation der Ladung begründet dann die magnetischen Eigenschaften des Elektrons.

Typischerweise wird diese Modellvorstellung allerdings im gleichen Atemzug wieder verworfen weil andere Eigenschaften des Elektrons wiederum überhaupt nicht zu diesem Modell passen wollen. Die dabei auftretenden Probleme kann man sich anschaulich klarmachen wenn man einige Eigenschaften des Elektrons auf den uns wohlbekannten Fußball überträgt:

• So ein Fußball müsste sich pausenlos drehen und das auch immer mit der gleichen Geschwindigkeit.
• Weiterhin könnte sich dieser Fußball nicht einmal in beliebige Richtungen drehen sondern hätte dafür nur genau zwei Richtungen zur Verfügung, nach links oder nach rechts. Die Rotationsachse so eines Fußballs könnte also nur entweder nach unten oder oben zeigen, niemals aber in eine andere Richtung.
• In welche Richtung der Fußball sich aktuell dreht würde sich erst in genau dem Moment entscheiden, in dem jemand versucht diese Drehrichtung festzustellen, z.B. durch eine Sichtkontrolle.
• Das Ergebnis so einer ersten Sichtkontrolle wäre zwangsläufig immer rein zufällig.
• Darauf folgende Sichtkontrollen aus dieser Richtung wären dann nicht mehr zufällig sondern ergäben immer die zuerst beobachtete Drehrichtung.
• Würde der Beobachter allerdings vor einer zweiten Sichtkontrolle ein wenig um den Fußball herumgehen, dann wäre das Ergebnis der zweiten Sichtkontrolle doch wieder zufällig, diesmal allerdings mit einer gewissen statistischen Tendenz.
• Diese Tendenz ließe sich so formulieren: Je weiter der Beobachter vor der zweiten Sichtkontrolle in Richtung der “Rückseite” des Fußballes läuft, desto wahrscheinlicher wird es dass er bei der zweiten Sichtkontrolle die jeweils andere Drehrichtung erblickt.
• Läuft der Beobachter exakt 180° bis zur “Rückseite” um den Fußball, so wird die zweite Sichtkontrolle in diesem Fall sogar mit Sicherheit die jeweils andere als die zuerst beobachtete Drehrichtung ergeben.
• Würde der Beobachter dann (müde von den vielen Versuchen) zur Abwechslung versuchen, die Größe des Fußballs auszumessen, so müsste er feststellen dass der Fußball unabhängig von der Präzision der Messung überhaupt keine räumliche Ausdehnung hätte sondern eigentlich nur ein einzelner Punkt wäre.

Bei solch absurd anmutenden Eigenschaften wird es für die Modellvorstellung einer rotierenden Elektronenkugel offensichtlich ganz ganz eng, Physiker sagen deswegen auch dass der Spin des Elektrons nur eine “intrinsische”, nicht weiter hinterfragbare Eigenschaft des punktförmigen Elektrons sei.

Man kann sich allerdings auch fragen, ob das doch sehr einfache und anschauliche Kugelmodell nicht vielleicht doch durch irgendeine Modifikation oder Erweiterung gerettet werden kann und in der Tat werden wir im Folgenden eine solche Modifikation des Kugelmodells kennenlernen und sehen, dass man damit auch die oben angedeuteten, höchst seltsame anmutenden Eigenschaften von Spin-Messungen anschaulich darstellen kann.

Allerdings soll an dieser Stelle auch gleich sehr deutlich darauf hingewiesen werden, dass das resultierende Modell zwar die Messwahrscheinlichkeiten einer Spin-Messung plausibel veranschaulichen kann, andere Eigenschaften des Elektrons aber nicht mit abgedeckt und deswegen auch nur als der Versuch verstanden werden darf, einen besonders unanschaulichen Teilaspekt der seltsamen Quantenmechanik durch eine einfache Modellvorstellung klassisch zu veranschaulichen und so auch Interessierten ohne eine mathematische Vorbildung zugänglich zu machen.

2. Drei zentrale Begriffe vorweg:

Um das im Folgenden vorgestellte Gedankenmodell kürzer und präziser beschreiben zu können, wollen wir zu Beginn drei wichtige Begriffe einführen:

2.1 Scheibenrotation und Kugelrotation

Wenn wir eine Münze in der Hand halten, so können wir diese im Prinzip auf die unterschiedlichsten Arten drehen. Weil zwei spezielle Varianten solcher Drehungen im weiteren Text noch eine größere Rolle spielen werden, geben wir diesen jeweils einen eigenen Namen:

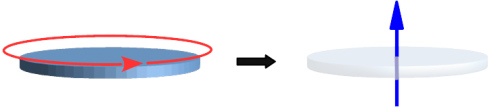
• Scheibenrotation: Ein Beispiel hierfür wäre eine Münze, die sich wie eine Schallplatte oder eine Frisbee-Scheibe dreht, unsere Namensgebung bezieht sich somit auf die Form der rotierenden Münze (siehe Abb. 1).
  

  Abb. 1: Beispiel für eine “scheibenrotierende” Scheibe, der Rotationskörper (rechts mit Rotationsachse) entspricht hier ebenfalls einer Scheibe und ist sogar identisch zur Ausgangsform (links).

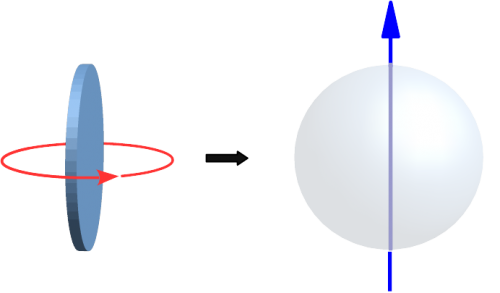
• Kugelrotation: Ein konkretes Beispiel hierfür wäre eine Münze, die wie ein Kreisel auf einer Tischplatte rotiert, hier bezieht sich die Namensgebung also auf die Kugelform einer kreiselnden Münze (siehe Abb. 2).
  

  Abb. 2: Beispiel für eine “kugelrotierende” Scheibe, der Rotationskörper (rechts mit blauer Rotationsachse) hat eine Kugelform und entspricht somit nicht mehr der Ausgangsform einer Scheibe (links)

2.2 Passiver Münzwurf: Ein idealisierter Münz-“Abwurf“

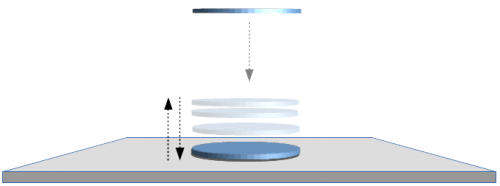
Wir wollen uns unter einem “passiven Münzwurf” eine spezielle Form des Münzwurfs vorstellen, bei der eine Münze mit einer bestimmten Ausrichtung aus geringer Höhe auf einen Tisch fallen gelassen wird und die Münze sowohl beim “Abwurf” als auch beim Fallen keinen zusätzlichen Drall oder Effet mehr bekommen darf.

Die Besonderheit dieses Münzwurfs liegt darin, dass eine so “abgeworfene” Münze im Flug ihre räumliche Ausrichtung nicht mehr ändert (den Luftwiderstand und andere Einflussfaktoren ignorieren wir mal großzügig) und deswegen mit genau jener Ausrichtung auf den Tisch aufprallt, welche sie auch vor dem Abwurf schon hatte (Abb. 3).

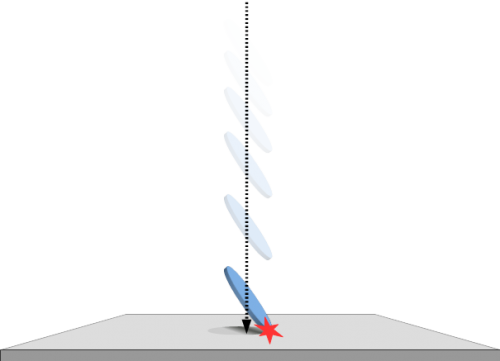
Abb. 3: Beim passiven Münzwurf prallt die Münze mit genau mit jener räumlichen Orientierung auf den Tisch auf, welche sie schon vor dem Abwurf hatte, die Münze dreht sich also nicht mehr im Flug.

Für spezielle Ausrichtungen der Münze vor dem Wurf kann man die entsprechenden Wurfwahrscheinlichkeiten nun direkt aus dem Modell ableiten:

• Münze waagrecht: Die Münze prallt also exakt waagrecht auf den Tisch auf und hüpft dann idealerweise nur noch auf und ab, da die zufallsbestimmenden Unebenheiten des Tisches und der Münze durch die breite Kontaktfläche der ganzen Münzseite ausgemittelt werden.
  Das Ergebnis eines solchen Wurfes ist also stets identisch zu der Ausrichtung der Münze vor dem Wurf (siehe Abb. 4) und somit nicht zufällig.
  

  Abb. 4: Passiver Münzwurf mit waagrechter Ausrichtung der Münze, das Ergebnis eines solchen Wurfes entspricht idealerweise immer der Ausrichtung der Münze vor dem Wurf

• Münze senkrecht: Weil die Münze so immer genau senkrecht auf den Tisch aufprallt, sind beide Wurfergebnisse (aus Symmetriegründen) gleich wahrscheinlich (siehe Abb. 5), das Ergebnis also immer rein zufällig.
  

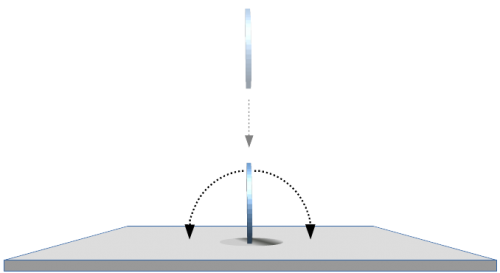
  Abb. 5: Passiver Münzwurf mit senkrechter Ausrichtung der Münze, das Ergebnis eines solchen Wurfes ist rein zufällig weil beide Ergebnisse gleich wahrscheinlich sind.

  Kleiner Hinweis: Die Möglichkeit einer nach dem Münzwurf auf dem Rand stehenden Münze wollen wir hier nicht berücksichtigen, beispielsweise indem wir für die entsprechenden Experimente immer eine Münze mit abgerundeten Rändern fordern.

In der folgenden Tabelle sind die jeweiligen Wurfwahrscheinlichkeiten und Durchschnittswerte nochmals zusammengefasst. Weil wir zusätzlich die beiden möglichen Wurfergebnisse KOPF und ZAHL mit den numerischen Werten 1 und -1 identifizieren, können wir auch die Durchschnittswerte und Einzelwurfwahrscheinlichkeiten durch Zahlenwerte angeben.

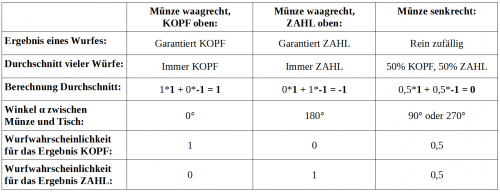
Tabelle 1: Abgeleitete Durchschnittswerte und Einzelwurfwahrscheinlichkeiten des passiven Münzwurfs.

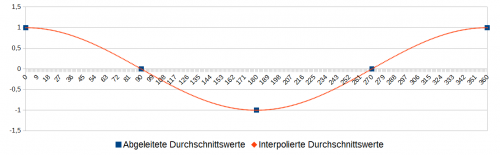
Die Durchschnittswerte für alle anderen Winkel α zwischen Münze und Tisch (eigentlich: zwischen der KOPF-Seite der Münze und der Tischplatte) können wir nun ausgehend von den oben abgeleiteten Werten einfach mit der Kosinus-Funktion “interpolieren” wie in Abb. 6 dargestellt.

Abb. 6: Interpolation der abgeleiteten Durchschnittswerte (blau) mit der Kosinus-Funktion (rot).

Die von dem Winkel α abhängigen Einzelwurfwahrscheinlichkeiten können dann für KOPF mit dem Ausdruck cos²(α/2) und für ZAHL über den Ausdruck sin²(α/2) berechnet werden (Abb. 7).

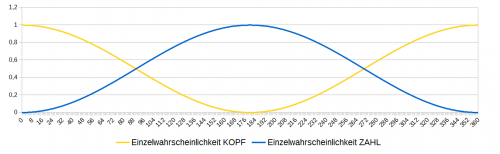
Abb. 7: Abhängig vom Winkel α zwischen Münze und Tisch berechnete Wurfwahrscheinlichkeiten für einen Einzelwurf.

Zusammenfassend könnte man also sagen dass der passive Münzwurf eine idealisierte Form eines Münzwurfs darstellt, dessen Wurfwahrscheinlichkeiten leicht und intuitiv erfasst werden können.

3. Aufbau des Gedankenmodells

Nach diesem etwas länglichen aber gleich noch sehr nützlichen Vorgeplänkel können wir uns jetzt endlich mit der Konstruktion des eigentlichen Gedankenmodells beschäftigen.

3.1 Erweiterung des Kugelmodells

Weiter oben haben wir die Modellvorstellung einer rotierenden Elektronenkugel angesprochen und gesehen, wie schnell diese etwa bei der Spin-Messung versagt.
Allerdings können wir die obigen Widersprüche umgehen, wenn wir die Modellvorstellung der rotierenden Elektronenkugel an einigen Stellen modifizieren und ausbauen:

• Rotierende Scheibe: Statt einer rotierenden Kugel stellen wir uns das Elektron in diesem Modell als eine geladene und scheibenrotierende Scheibe vor.
• Hohle Kugel: Um einen direkten Zugriff auf die Elektronenscheibe zu verhindern verfrachten wir diese ins Zentrum einer hohlen, nicht direkt zugänglichen Kugel.
• Messapparat: In Ermangelung eines direkten Zugriffs müssen wir für eine Spin-Messung einen dedizierten Spin-Messapparat zur Verfügung stellen.

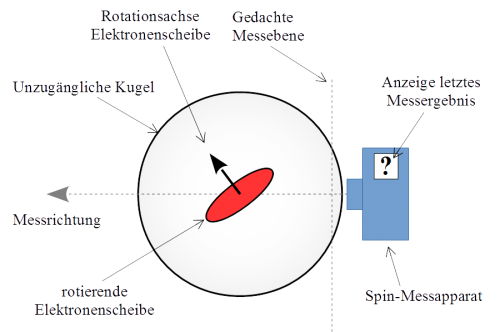
Abb. 8: Komponenten des Gedankenmodells. Der Spin-Messapparat (blau) kann zur Messung der Ausrichtung der Elektronenscheibe (rot) in der Kugel von außen an der Kugel (grau) angebracht und aktiviert werden.

3.2 Spin-Messung aus Sicht des Messapparats

Aus Sicht des Messapparats besteht eine Spin-Messung im Gedankenmodell aus drei Einzelschritten:

1. Ausrichtung des Messapparats durch Anbringung an einer beliebigen Stelle auf der Kugelaußenwand (Abb. 9.a).
2. Durchführung einer Messung (angezeigt durch die gelbe Spitze) und Anzeige des Ergebnisses (Abb. 9.b).
3. Deaktivierung des Messapparats und Anzeige des letzten Messergebnisse bis zur nächsten Messung (Abb. 9.c).

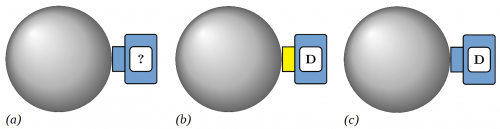
Abb. 9: Die wesentlichen Schritte einer Spin-Messung aus Sicht des Messapparats, der Messapparat hat dabei definitionsgemäß keine Kenntnis von der Scheibe im Inneren der Kugel.

3.3 Spin-Messung aus Sicht der Elektronenscheibe

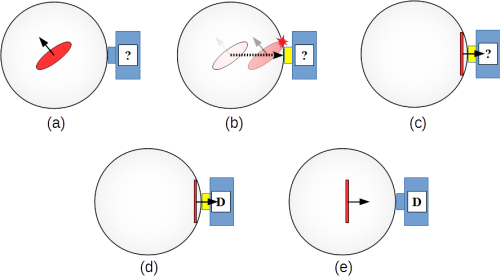
1. Der Messapparat wird außen an der Kugel angebracht (Abb. 10.a).
2. Der Messapparat wird eingeschaltet (erkennbar an der gelben Spitze) und beginnt dann, die Elektronenscheibe aus dem Zentrum der Kugel in Richtung des Messapparats zu ziehen bis diese schließlich mit der Kugelinnenwand kollidiert (Abb. 10.b).
3. Dort soll die Scheibe dann analog zu einem passiven Münzwurf und mit den entsprechenden Wahrscheinlichkeiten nach einigen pseudozufälligen Aufsetzern schlussendlich mit dem Rand an der Kugelinnenwand anliegend zur Ruhe kommen (Abb. 10.c).
4. Der Spin-Messapparat soll dann und nur dann messen können, in welche Richtung sich die Scheibe gerade dreht (Abb. 10.d):
   • Dreht sich die Scheibe aus Sicht des Messapparats im Uhrzeigersinn, so bezeichnen wir dieses Messergebnis als UP.
   • Dreht sich die Scheibe aus Sicht des Messapparats gegen der Uhrzeigersinn, so bezeichnen wir dieses Messergebnis analog als DOWN.
5. Nach der Messung schaltet sich der Messapparat ab und die Scheibe soll dann mit ihrer neuen Ausrichtung wieder ins Zentrum der Kugel zurückwandern (Abb. 10.e).

Abb. 10: Einzelschritte einer Spin-Messung aus Sicht des Elektrons.

Wichtige Randbedingungen:

• Um das Zurückwandern der Elektronenscheibe in das Kugelzentrum am Ende der Messung zu begründen, fordern wir dafür einfach ein zusätzliches Kraftfeld, das wir aber nicht näher spezifizieren müssen.
• Weder der Messapparat noch das abstrakte Kraftfeld sollen die Ausrichtung der Elektronenscheibe ändern können, sie sollen also lediglich die Position der Scheibe in der Kugel verändert können.
• Somit kann die Ausrichtung der Scheibe nur noch im Rahmen einer Messung durch die Kollision mit der Kugelinnenwand geändert werden.

Hinweis: Durch diese Konstruktionsart kann das Gedankenmodell prinzipiell auch als eine 3D-Version des passiven Münzwurfs angesehen werden: Der Messapparat ersetzt die Schwerkraft, die Kugelinnenwand ersetzt die Tischplatte und das Ablesen des Ergebnisses wird hier nicht durch einen Beobachter sondern durch den Messapparat durchgeführt.

3.4 Namenskonventionen

• Phase: Momentaner Grad der Scheibenverdrehung der scheibenrotierenden Elektronenscheibe.
• Zustand: Momentane (deterministische) Ausrichtung der Elektronenscheibe in der hohlen Kugel plus Phase der Elektronenscheibe.
• Messung: Die Elektronenscheibe wird vom Messapparat in Richtung Kugelinnenwand gezogen und kollidiert schlussendlich analog zum passiven Münzwurf mit dieser, was in der Folge zu einem (meist) zufälligen Messergebnis führt.
• Quantisierung: Weil im Gedankenmodell bei einer Spin-Messung nur zwei mögliche Rotationsrichtungen gemessen werden können, bezeichnen wir den Elektronenspin als quantisiert.
• Phaseninvarianz: Da sich Form und Ausrichtung der Elektronenscheibe durch eine Scheibenrotation nicht ändern, übt diese im Sinne der Mechanik des passiven Münzwurfs keinen Einfluss auf den Ausgang einer Spin-Messung aus, wir bezeichnen die Spin-Messung deswegen als phaseninvariant.
• Zustand II: Wegen der Phaseninvarianz einer Spin-Messung kann der Zustand im Gedankenmodell oft auch nur als die Ausrichtung der Elektronenscheibe in der Kugel verstanden werden.

4. Einige Gedankenexperimente

4.1 Spin-Präparation

Physik:

• Das Ergebnis der ersten Messung eines Elektronenspins ist immer rein zufällig.
• Aus diesem Grund kann und darf vor einer ersten Messung auch keine Aussage über den Elektronenspin gemacht werden. Man sagt deswegen auch, dass der Zustand des Spins durch die erste Spin-Messung überhaupt erst präpariert und somit bekannt gemacht wird.

Gedankenmodell:

• Weil die Elektronenscheibe in der hohlen Kugel per Definition nur durch die Verwendung des Spin-Apparats beeinflusst werden kann, kann auch hier vor einer ersten Messung grundsätzlich keine Aussage über die Ausrichtung der Elektronenscheibe in der Kugel getroffen werden.
• Weil zusätzlich die erste Spin-Messung die Elektronenscheibe in fast allen Fällen neu ausrichtet, ist es auch hier zutreffend zu sagen, dass die erste Messung den Spin überhaupt erst festlegt und mithin präpariert, weil die Ausrichtung der Elektronenscheibe jetzt auch außerhalb der Kugel bekannt gemacht wurde.

Abb. 11: Beispielhafte Präparation des Spins im Gedankenmodell im Zustand UP.

4.2 Wiederholbarkeit einer Spin-Messung

Physik:

• Die Spin-Messung des Elektrons wird wiederholbar genannt weil nach der Spin-Präparation jede weitere Messung aus der gleichen Richtung mit Sicherheit wieder den präparierten Wert liefern wird.
• Die Wiederholbarkeit endet erst dann, wenn erstmalig eine Messung aus einer anderen Richtung (ungleich 180°) vorgenommen wird.

Gedankenmodell:

• Nach der Präparation ist die Elektronenscheibe genau waagrecht zum Messapparat ausgerichtet und gemäß dem passiven Münzwurf wird jede weitere Messung aus dieser Richtung diese Ausrichtung auch nicht mehr ändern, die Spin-Messung ist also auch im Gedankenmodell wiederholbar (Abb. 12).
• Wird allerdings zwischendurch eine Messung aus einer anderen Richtung (ungleich 180°) vorgenommen, so geht diese Wiederholbarkeit verloren weil die Elektronenscheibe durch so eine Messung zwangsläufig neu ausgerichtet wird.

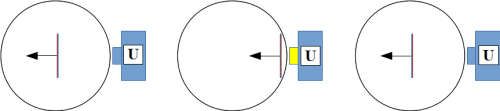
Abb. 12: Wiederholbare Spin-Messung im Gedankenmodell gemäß den Wahrscheinlichkeiten des passiven Münzwurfs.

4.3 Spin-Messung aus der entgegengesetzten Richtung

Physik:

Wird nach der Präparation des Spins eine Spin-Messung aus der entgegengesetzten Richtung durchgeführt, so ergibt diese Messung mit Sicherheit den jeweils nicht präparierten Wert.

Gedankenmodell:

Auch im Gedankenmodell ergibt sich gemäß dem passiven Münzwurf durch so eine Messung keine Neuausrichtung der Elektronenscheibe, die Scheibe ist also auch von der gegenüberliegenden Seite aus waagrecht zum Messapparat ausgerichtet (siehe Abb. 13).

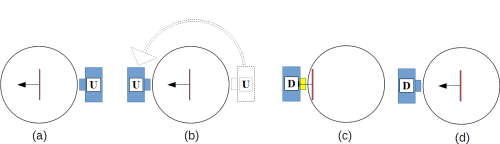
Abb. 13: Eine Spin-Messung aus entgegengesetzter Richtung ändert im Gedankenmodell nicht die Ausrichtung der Elektronenscheibe, die Ursprungsmessung bleibt somit wiederholbar.

4.4 Unscharfe und maximal unscharfe Spin-Messung

Physik:

• In der Physik spricht man von einer unscharfen Spin-Messung, wenn der Ausgang der Messung zufällig ist.
• Wenn darüber hinaus beide Messergebnisse gleich wahrscheinlich sind, spricht man auch von einer maximal unscharfen Spin-Messung.

Gedankenmodell:

• Wenn im Gedankenmodell die Elektronenscheibe vor einer Messung nicht waagrecht zum Messapparat ausgerichtet ist, so ist das Ergebnis der nächsten Spin-Messung zwangsläufig zufällig, die Messung mithin unscharf.
• Ist die Elektronenscheibe zusätzlich genau senkrecht zum Messapparat ausgerichtet, so sind beide Messergebnisse gemäß dem passiven Münzwurf gleich wahrscheinlich und die Folgemessung mithin maximal unscharf (Abb. 14.b).

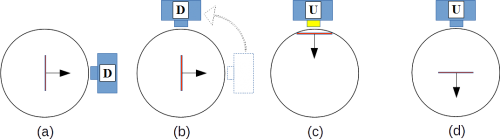
Abb. 14: Beispiel für eine maximal unscharfe Spin-Messung (b) nach einer Drehung des Messapparates um 90°.

4.5 Zerstörung eines präparierten Zustandes

Physik:

• Man spricht in der Physik von der Zerstörung eines präparierten Spin-Zustandes, wenn nach der Präparation des Elektronenspins eine Messung aus einer anderen Richtung (ungleich 180°) vorgenommen wird.
• Der Begriff “Zerstörung” bezieht sich dabei auf den Umstand, dass eine solche Folgemessung zwangsläufig den Spin-Zustand ändert, der ursprünglich präparierte Zustand geht deswegen durch so eine Messung verloren.

Gedankenmodell:

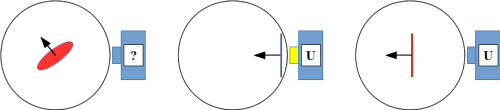
Auch im Gedankenmodell bewirkt eine zwischenzeitliche Messung aus einer anderen Richtung (ungleich 180°) die Zerstörung eines präparierten Zustandes, einfach weil die Elektronenscheibe durch eine solche Messung zwangsläufig neu ausgerichtet wird und ein Folgemessung aus der Ursprungsrichtung somit auch andere Messwahrscheinlichkeiten aufweist (Abb. 15).

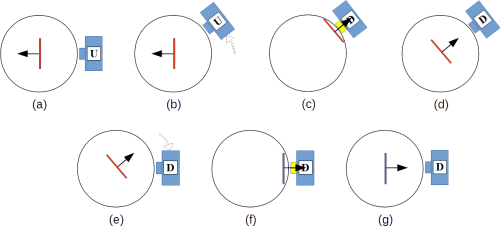
Abb. 15: Beispielhafte Zerstörung (15.b bis 15.d) des präparierten Zustandes (15.a) durch eine Spin-Messung aus einer anderen Richtung (hier ca. 40°). Eine erneute Messung aus der Ursprungsrichtung (15.e bis 15.g) hat somit zwangsläufig andere Messwahrscheinlichkeiten als direkt nach der Präparation.

5. Ausblick

Einige interessante Aspekte des Gedankenmodells mussten wegen Platzmangel leider außen vor bleiben, hier wenigstens einige Stichwörter dazu:

• Mit dem Gedankenmodell können auch die Erwartungswerte maximal verschränkter Elektronenpaare veranschaulicht werden (besonders einfach funktioniert das im Fall des Singulett-Zustandes).
• Weil es ein 1:1-Mapping zwischen der mathematischen Beschreibung des Spins und dem Gedankenmodell gibt, kann der mathematische Formalismus so auch einem mathematischen Laien beispielhaft vermittelt werden.
• Die zeitliche Entwicklung des Spins kann durch entsprechende Kugelrotationen der (strukturell unveränderlichen) Elektronenscheibe in der Kugel dargestellt werden.
• Die bei der Widerlegung der Bell’schen Ungleichung verwendete Mess-Methodik kann mit dem Gedankenmodell leicht und anschaulich nachvollzogen werden (kommt dabei allerdings ein bisschen wie ein Äpfel/Birnen-Vergleich rüber).

Vielleicht ist es sogar möglich, das Gedankenmodell noch für weitere Veranschaulichungen zu benutzen, hier zum Abschluss noch einige halbgare Ideen für mögliche Versuche einer Erweiterung:

• Möglicherweise kann man mit dem Scheibenmodell neben Fermionen (Spin-1/2-Teilchen wie das Elektron) auch Bosonen (Spin-1-Teilchen wie das Photon) veranschaulichen, indem man Bosonen als nicht scheibenrotierende Scheiben modelliert.
• Die unterschiedlichen Eigenschaften von scheibenrotierenden und nicht scheibenrotierenden Scheiben könnte man dann auch dazu benutzen, das Verhältnis der unterschiedlichen Drehsymmetrien von Bosonen und Fermionen zu plausibilisieren:
  • Eine nicht rotierende Scheibe sieht bereits nach einer Kugelrotation von 180° wieder so aus wie vor der Drehung.
  • Eine scheibenrotierende Scheibe hingegen sieht wegen der unterschiedlichen Ausrichtungen der Rotationsachse erst nach einer Kugelrotation von 360° wieder so aus wie vor der Drehung.
• Wenn man die Geschwindigkeit der Kugelrotation einer Scheibe mit der Energie des Teilchens identifizieren würde (die entsprechenden Formeln würden das denke ich hergeben), dann könnte man eine Energie-Quantisierung durch eine Energie-Messmechanik analog zur Spin-Messung einfach und plausibel veranschaulichen.
• Wenn man sich weiterhin eine Ortsmessung eines Elektrons so vorstellt, dass die Elektronenscheibe dafür senkrecht auf der Kugelinnenwand kreiseln muss, dann hätte man dadurch eventuell die Möglichkeit, die Orts- und Impulsunschärfe von Elektronen einfach durch eine unterschiedliche Ausrichtung der Elektronenscheibe für die jeweilige Messung zu motivieren.
• Zuletzt könnte man mit so einer Mechanik der Ortsmessung auch noch den Versuch unternehmen, den punktförmigen Charakter des Elektrons im Gedankenmodell als einen Quantisierungseffekt zu veranschaulichen:
  Wenn nämlich die Elektronenscheibe senkrecht auf der Kugelinnenwand kreiselt, dann gibt es unabhängig davon wie genau man misst immer nur einen einzigen Punkt, an dem die Elektronenscheibe die Kugelinnenwand berührt (wenn die Elektronenscheibe entweder wie unsere Münze abgerundete Ränder hat oder aber infinitesimal dünn ist).
  Eine entsprechende Messlogik vorausgesetzt würde sich die Elektronenscheibe dann außerhalb der Kugel immer nur als ein separater Punkt manifestieren, ihre räumliche Form und Ausdehnung würden also im Rahmen einer Messung überdeckt werden und könnten sich höchstens noch indirekt (etwa durch entsprechende Unschärfen) manifestieren.

Ob man aber schlussendlich zumindest eine dieser Ideen halbwegs widerspruchsfrei mit dem bestehenden Gedankenmodell verheiraten kann, ist mir bisher noch nicht klar, ggf. muss ich dann vielleicht doch noch mal irgendwann einen zweiten Blog verfassen…

Dieser Artikel ist Teil des ScienceBlogs Blog-Schreibwettbewerb 2017. Informationen zum Ablauf gibt es hier. Leserinnen und Leser können die Artikel bewerten und bei der Abstimmung einen Preis gewinnen – Details...