Anlässlich der vor kurzem erfolgten Eröffnung des „AfD-Meldeportals“ für unerwünschte Lehrinhalte in meiner Wahlheimat Sachsen-Anhalt gibt es im „Frischen Wind“ heute mal eine kleine Rechenübung aus dem Bereich der Wahrscheinlichkeitslehre (Niveau 11./12. Klasse) für alle subversiven Lehrerinnen und Lehrer da draußen.
Die Besucherschaft eines Musikfestivals besteht zu 90% aus Angehörigen der Mehrheit sowie zu 10% aus Angehörigen einer Minderheit. Am Eingang zum Festgelände werden verdachtsunabhängige Kontrollen nach mitgeführten Drogen durchgeführt. Führt ein für die Kontrolle ausgewählter Besucher oder eine Besucherin tatsächlich Drogen mit sich, werden diese mit an Sicherheit grenzender Wahrscheinlichkeit auch entdeckt. Während nur jeder zehnte Angehörige der Mehrheit kontrolliert wird, muss sich jeder zweite Angehörige der als „krimineller“ geltenden Minderheit einer Kontrolle unterziehen. Tatsächlich ist der Anteil an Drogenkonsumenten in beiden Personengruppen mit 5% exakt gleich hoch.
Am nächsten Tag findet sich in der Presseberichterstattung zum Festival der folgende Satz:
„Obwohl Angehörige der Minderheit lediglich 10% der Besucherschaft ausmachten, waren sie für über 35% der an diesem Abend festgestellten Drogendelikte verantwortlich.“
Ist dieses Ergebnis rechnerisch plausibel?
Die Frage nach der rechnerischen Plausibilität der Zeitungsaussage lässt sich auch so formulieren: Mit welcher Wahrscheinlichkeit gehört eine zufällig kontrollierte Person der Minderheit an, wenn sie eines Drogendelikts überführt wurde? Es darf daher analog zur Logik des Satz von Bayes gerechnet werden (detaillierte Einführung siehe hier, praktisches Anwendungsbeispiel siehe hier). Vereinfacht formuliert ergibt sich bei einer exemplarischen Besucherzahl von 10.000 Menschen:
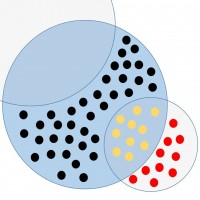
- Von 9.000 Angehörigen der Mehrheit führen 450 (5%) Drogen mit sich. Da 10% der Angehörigen der Mehrheit zufällig kontrolliert werden, ist in dieser Gruppe mit etwa 45 erfassten Delikten zu rechnen.
- Von 1.000 Angehörigen der Minderheit führen 50 (ebenfalls 5%) Drogen mit sich. Da jedoch 50% der Angehörigen der Minderheit zufällig kontrolliert werden, ist in dieser Gruppe mit etwa 25 erfassten Delikten zu rechnen.
Tatsächlich wurden also 25 von 70 (35,7%) der an diesem Abend insgesamt erfassten Delikte von Angehörigen der Minderheit begangen. Die in der Presse getroffene Aussage ist somit zumindest rechnerisch korrekt. Selbstverständlich kann man auf Basis der gleichen Zahlen aber auch zu einem inhaltlich gänzlich anderen Fazit gelangen:
- Von den 900 (10%) kontrollierten Angehörigen der Mehrheit führten 45 (5%) Drogen mit sich, von den 500 (50%) kontrollierten Angehörigen der Minderheit führten 25 (5%) Drogen mit sich. Der Hang zur Drogenkriminalität ist somit in beiden Gruppen offenbar gleich hoch.
Man sieht schon: Welche Schlüsse man aus den Ergebnissen der verdachtsunabhängigen Kontrollen zieht, hängt wesentlich davon ab, ob sämtliche relevanten Zahlen (d.h. auch die Anzahl der ohne einen Drogenfund kontrollierten Personen sowie deren Aufteilung auf Mehrheit und Minderheit) vorliegen, oder ob lediglich eine selektive Auswahl (“x Delikte insgesamt, davon y% verübt durch Angehörige der Minderheit”) weitergegeben und/oder bewertet wird. Der sich aus letzterem ergebende Teufelskreis ist offensichtlich: Eine als höher wahrgenommene Neigung zu kriminellem Verhalten wird letztlich zu einem noch stärkeren Kontrolldruck und damit zur wiederholten Selbstbestätigung dieser verzerrten Wahrnehmung führen.
Und ja – das ist ein echtes Problem: In den USA werden beispielsweise Afro-Amerikaner deutlich häufiger als weiße Amerikaner wegen des möglichen Besitzes von Marihuana kontrolliert, obwohl alle vorliegenden Zahlen darauf hinweisen, dass die Nutzung von Marihuana unter weißen und Afro-Amerikanern ähnlich weit verbreitet ist. Im Ergebnis ist die Wahrscheinlichkeit dafür, dass ein Afro-Amerikaner wegen eines Marihuana-Delikts vor Gericht verurteilt wird, fast vier Mal so hoch wie die Wahrscheinlichkeit dafür, dass ein weißer Amerikaner für das gleiche Vergehen belangt wird.


Kommentare (27)