Die Quantenmechanik ist schwer zu verstehen, darin sind sich wohl alle einig. (Naja, fast alle – ich kenne jemanden, der das anders sieht und die QM einfacher als die klassische Physik findet…) Und wenn ich hier im Blog über Quantenmechanik schreibe, dann versuche ich jedesmal wieder, bestimmte Grundlagen zu erklären, jedesmal mit leicht anderen anschaulichen Beispielen. Wenn ich mich an die Zeit zurückerinnere, in der ich noch nicht studiert habe, dann war es damals so, dass ich wieder und wieder populärwissenschaftliche Darstellungen lesen konnte, jede war ein bisschen anders, alle waren irgendwie ähnlich, aber keine gab nir das Gefühl, es wirklich verstanden zu haben.
Ich vermute, dass das daran liegt, dass anschauliche Erklärungen (beispielsweise mit Quantentalern) das Problem, haben, dass man sie zwar nachvollziehen kann, man kann sie aber nur schwer auf andere Situationen übertragen und von ihnen aus weiterdenken. (Es ist ja ein häufiges Phänomen in den Diskussioen hier auf dem Blog, dass KommentatorInnen verwirrt sind, weil sie eine anschauliche Erklärung, die eben nur bedingt allgemeingültig ist, weiterzudenken versuchen und dann auf Widersprüche stoßen.)
Physikbücher über Quantenmechanik sind allerdings auf der anderen Seite voll von Mathematik – und man lernt nicht nur etwas über quantenmechanische Zustände, sondern meist auch noch Dinge wie das Lösen von partiellen Differentialgleichungen mit irgendwelchen Ansatzfunktionen, so dass die Physik oft hinter der Mathematik verschwindet.
Gibt es einen Mittelweg zwischen diesen beiden Extrema – Quantentaler auf der einen Seite, Differentialgleichungen auf der anderen? In diesem Text will ich versuchen, so einen Weg zu finden und den Begriff des quantenmechanischen Zustandes einzuführen, und zwar so, dass die Erklärungen keine Analogien sind. Ich habe keine Ahnung, ob das so klappt – deswegen bitte ich vor allem diejenigen, die keine PhysikerInnen sind, um Anmerkungen oder Kommentare. Wo klemmt’s, wo war es unverständlich, wo fehlt etwas? Wenn’s denn einigermaßen klappt, dann hoffe ich, dass ich in ein oder zwei weiteren Teilen dahin komme, auch solche Dinge wie Quantenverschränkung so zu erklären, dass ihr sie selbst wirklich nachvollziehen (und nicht nur staunend ansehen) könnt.
Quantenmechanische Zustände
Ein Teilchen der klassischen Physik ist immer in einem bestimmten Zustand. Es hat beispielsweise einen bestimmten Ort (das Teilchen ist jetzt gerade “hier”) und zusätzlich auch eine bestimmte Geschwindigkeit (es fliegt nach “dort”).
In der Quantenmechanik ist das anders. Betrachten wir zunächst mal das Teilchen nur in einem einzigen Moment – dann müssen wir uns über seine Geschwindigkeit erst mal keine Gedanken machen, sondern können uns auf seinen Ort konzentrieren. Um die Sache noch übersichtlicher zu halten, erlauben wir unserem Teilchen erst einmal nur zwei Möglichkeiten für den Ort – es kann entweder “hier” sein oder “da”. Es hat sich eingebürgert, Zustände in der Quantenmechanik in spezielle Klammern zu schreiben, damit man gleich weiß, dass das, was man meint, ein Zustand ist. Der Zustand “hier” wird geschrieben als |hier>, der Zustand “da” als |da> (und allgemein der Zustand “blubb” als |blubb> ).
In der klassischen Physik gibt es jetzt (in unserem hypothetischen Szenario) genau diese beiden Möglichkeiten für den Zustand des Teilchens: Entweder ist es “hier” oder es ist “da”, eine andere Möglichkeit gibt es nicht.Wenn wir wollen, können wir das mathematisch so aufschreiben:
|Klassischer Zustand> = 1 |hier> + 0 |da> oder 0|hier> + 1 | da>
Entweder ist der Zustand |hier>, dann multipliziere ich eine Null an den |da>-Zustand (irgendwas mal Null ist ja immer Null, das gilt auch für Zustände), oder es ist andersherum.
Allgemein kann ich das auch so umschreiben:
|Klassischer Zustand> = a |hier> + b |da> , mit entweder a=1,b=0 oder a=0,b=1.
Das ist natürlich ziemlich umständlich und ergibt in der klassischen Physik wenig Sinn.
In der Quantenmechanik ist es anders: Es gibt nicht bloß zwei mögliche Zustände eines Teilchens, sondern unendlich viele – es gibt Mischzustände, bei denen das Teilchen sich so verhält, als wäre es gleichzeitig “hier” und “da”. Die kann ich genauso schreiben
|QM-Zustand> = a |hier> + b |da>,
aber a und b sind jetzt nicht einfach 1 oder 0, sondern sind jetzt beliebige Zahlen, die lediglich folgende Eigenschaft erfüllen müssen:
a²+b²=1
Der klassische Zustand mit a=1,b=0 (oder umgekehrt) erfüllt diese Regel, er ist also auch in der QM ein zulässiger Zustand. In der Quantenmechanik allerdings wäre auch a=b=1/√2 ein erlaubter Zustand, denn dann ist
Genau genommen sind die Zahlen a und b komplexe Zahlen, keine gewöhnlichen reellen Zahlen. Diese kleine Komplikation spielt hier erst einmal keine Rolle, deswegen verbanne ich sie hinter dieses Warnschild. Komplexe Zahlen habe ich mal ausführlich hier erklärt.
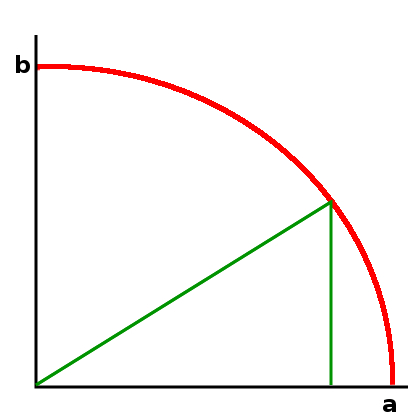
Man kann sich die Extra-Bedingung für a und b auch leicht grafisch veranschaulichen: a²+b²=1 ist gerade die Formel für einen Kreis mit Radius 1:
In der klassischen Physik sind also nur die beiden Zustände auf den Achsen erlaubt (a=1, b=0 und umgekehrt), aber ein quantenmechanischer Zustand kann sich irgendwo auf der roten Linie befinden. Es gibt also in der Quantenmechanik unendlich viele verschiedene Möglichkeiten für ein System, dass klassisch nur zwei mögliche Zustände hat. (Und das ist auch genau der Grund, warum so viel über Quantencomputer geredet wird: Ein klassisches Bit hat entweder den Wert 0 oder den Wert 1, ein qu-bit dagegen kann sich in allen möglichen Überlagerungszuständen befinden.) Diese einfache grafische Darstellung ist allerdings nur bei einem Zwei-Zustands-System wirklich hilfreich (und auch da ist sie nicht ganz exakt, weil – wie oben hinter dem Warnschild erläutert – a und b komplexe Zahlen sein können). Deswegen wird sie in dieser Form selten angewandt, zur Illustration des Unterschieds zwischen einem klassischen und einem Qm-System ist sie aber trotzdem hilfreich.
Wenn unser Teilchen an drei Orten sein kann (also auch noch |dort>), dann sieht der Zustand entsprechend aus:
|QM-Zustand> = a |hier> + b |da> + c | dort>,
und jetzt gilt ganz entsprechend
a²+b²+c²=1 (Das könnte man grafisch mit einer Kugel veranschaulichen, wenn man will…)
Fazit: Ein quantenmechanisches System kann sich in einer Überlagerung aus unterschiedlichen Zuständen befinden.
Die Zahlen a,b,c usw. nennt man die Wahrscheinlichkeitsamplitude des jeweiligen Zustands. In meiner Formel oben ist a also die Wahrscheinlichkeitsamplitude für den Zustand |hier>, b die für den Zustand |da>. In der klassischen Physik ist eine der Wahrscheinlichkeitsamplituden gleich eins, alle anderen sind null, deswegen ergibt diese Zustands-Schreiberei nicht viel Sinn. In der QM allerdings sind beliebige Werte für die Wahrscheinlichkeitsamplituden möglich (allerdings muss die obige Formel gelten: Die Summe der Quadrate aller Amplituden muss genau eins ergeben, warum, sehen wir noch).
Bevor es weitergeht, hier eine kleine Übung, damit ihr seht, ob ihr auch alles bis hier verstanden habt:
Ein quantenmechanisches Teilchen soll sich in einem von 4 möglichen Zuständen befinden können, die wir von |1> bis |4> durchnummerieren. Welcher der folgenden Zustände ist möglich, welcher nicht:
a) Ist möglich, denn (1/2)²=1/4, die Summe aller vier Amplitudenquadrate ist also gleich 1.
b) Ist auch möglich, denn die Summe der Amplitudenquadrate ist wieder gleich 1 – die Amplituden für die Zustände |2> und |4> sind gleich Null.
c) Hier werden zwei Zustände multipliziert. Das ist so nicht möglich, die unterschiedlichen Zustände müssen immer addiert werden. (Wenn man allerdings mehrere Teilchen betrachtet, kann man diese Schreibweise verwenden, sie besagt dann, dass sich das eine Teilchen im Zustand |1> und das andere im Zustand |2> befindet.)
d) Das geht auch nicht, den die Summe der Quadrate der Amplituden ist 7/9, also nicht gleich 1.
Die Bedeutung der Überlagerung
O.k., wir haben gesehen, dass ein Teilchen (oder überhaupt jedes quantenmechanische System) sich in einem Überlagerungszustand befinden kann. Aber was bedeutet das? Wir beobachten ja keine Objekte, die gleichzeitig hier und da sind – wenn ich hinschaue, ist meine Computertastatur genau an einer Stelle, sonst wäre das Tippen von Blogtexten auch ziemlich schwierig.
Tatsächlich ist dieser (scheinbare) Widerspruch das große Rätsel der Quantenmechanik: Wie kann man die quantenmechanische Überlagerung von Zuständen in Einklang bringen mit Messungen, in denen sich Teilchen nach den Regeln der klassischen Physik verhalten, und deshalb in einem eindeutigen, klassischen Zustand sind? Das ist das berühmte Messproblem der Quantenmechanik, das in ganz unterschiedlicher Weise interpretiert werden kann. Über die Interpretation kann man sich beliebig lange streiten – zum Glück ist für alle praktischen Zwecke klar, was in einer bestimmten Situation passiert.
Ich stelle mich hier deshalb erst einmal auf einen pragmatischen Standpunkt: Führt man eine Messung an einem Quantenobjekts durch, dann beeinflusst diese Messung den Zustand so, dass das Objekt hinterher in dem gemessenen Zustand ist. Klingt kompliziert? Nehmen wir wieder unser Beispiel von oben, ein Teilchen in einem Zustand
a |hier> + b |da>
Wenn ich jetzt gucke, wo das Teilchen tatsächlich ist, dann finde ich es entweder hier oder da (es gibt keine halben Teilchen, die ich messen könnte). Hinterher (also nach der Messung) ist der Zustand also entweder |hier> oder |da>, es ist also entweder a=1 oder b=1 (und der andere Zahlenwert ist Null). Also: Nach einer Messung ist das System in dem Zustand, der zur Messung passt.
Das gilt auch, wenn sich das System in einer Überlagerung aus mehr als zwei Zuständen befindet. Messe ich also bei einem Teilchen im Zustand
a |hier> + b |da> + c | dort>
das Teilchen “hier”, dann ist es hinterher im Zustand |hier>.
Etwas komplizierter wird die Sache, wenn man bei der Messung nur eine Teilinformation bekommt. Schaue ich beispielsweise bei meinem Teilchen, das in der Drei-Zustand-Überlagerung ist, “hier” nach und stelle fest, dass es nicht “hier” ist, dann ist es hinterher in einem Überlagerungszustand aus |da> und |dort>:
b’ |da> + c’ | dort>
Die Zahlen b’ und c’ müssen jetzt (weil ja die Wahrscheinlichkeitsamplitude für den |hier>-Anteil Null ist) wieder 1 ergeben, wenn man sie quadriert und addiert. Dabei ändert sich das Verhältnis der beiden nicht, es ist also b/c=b’/c’. Nehmen wir als Beispiel an, dass vorher die drei Koeffizienten die Werte
hatten (ihr könnt euch schnell überzeugen,dass das ein zulässiger Zustand ist, weil die Summe der Quadrate 1 ergibt), dann haben wir hinterher die Werte
(Wer mag, darf es als kleine Übung gern nachrechnen.)
Die allgemeine Regel für das, was bei einer Messung mit einem Überlagerungszustand passiert, geht also so:
Schreibe den Überlagerungszustand hin. Setze alle Wahrscheinlichkeitsamplituden gleich Null, die nicht zur Messung passen. Passe die übrigen Wahrscheinlichkeitsamplituden so an, dass die Summe ihrer Quadrate immer noch 1 ergibt und dass ihr Verhältnis (oder ihre Verhältnisse) unverändert bleibt.
Bei einer Messung passiert also etwas Seltsames – der Zustand eines Systems ändert sich durch die Messung schlagartig. Das ist bereits die “spukhafte Fernwirkung”, über die sich Einstein so echauffiert hat – stellt euch vor, “hier” wäre genau hier, und “da” wäre bei Alpha Centauri. Wenn ihr das Teilchen jetzt hier entdeckt, dann ändert sich der Zustand bei Alpha Centauri schlagartig, obwohl das ein paar Lichtjahre sind und sich doch keine Signale mit Überlichtgeschwindigkeit ausbreiten dürfen.
Mit einem einzigen Teilchen lässt sich das allerdings nicht ohne weiteres nachweisen – es könnte ja sein, dass wir den Zustand des Teilchens einfach vorher nicht richtig kannten und in Wahrheit war es die ganze Zeit schon hier und nicht da. Um nachzuweisen, dass es diesen seltsamen Quanteneffekt wirklich gibt, braucht man mehrere Teilchen, deren Zustände miteinander gekoppelt werden – das ist die berühmte “Verschränkung”, aber dazu schreibe ich ein andermal mehr.
Die Bedeutung der Wahrscheinlichkeitsamplituden
Bisher waren unsere “Wahrscheinlichkeitsamplituden” a,b und c einfach nur irgendwelche Zahlen. Ich habe mich aber davor gedrückt zu sagen, was sie bedeuten. Der Name “Wahrscheinlichkeitsamplitude” legt bereits nahe, dass sie etwas mit Wahrscheinlichkeiten zu tun haben (sonst wäre es ein wirklich wirklich saublöder Name) und so ist es auch. Die Amplituden selbst sind allerdings nicht die Wahrscheinlichkeiten, sondern ihre Quadrate sind es.Messe ich den Zustand eines Teilchens, so bekomme ich die jeweils möglichen Werte mit der entsprechenden Wahrscheinlichkeit, also im Beispiel oben a² für den Zustand |hier> und b² für den Zustand |da>. Welchen Zustand ich messe, wenn ich nur eine einzige Messung mache, weiß ich natürlich vorher nicht, das entscheidet der Zufall, und bisher ist es noch niemandem gelungen, hinter diesem Zufall ein tieferes Gesetz zu finden. Bei einer Einzelmessung weiß ich also nicht, was rauskommt – es sei denn, eine der Wahrscheinlichkeitsamplituden ist gleich 1 (und die anderen gleich Null), dann ist die Sache klar.
Bin ich also im Überlagerungszustand aus dem Beispiel oben:
dann ist die Wahrscheinlichkeit für jeden Zustand gleich 1/2²=1/4, es sind also alle Zustände gleich wahrscheinlich.
Ihr seht jetzt auch, warum die Regel, dass die Amplitude den Wert Null bekommt, wenn man weiß, dass man einen Zustand nicht gemessen hat, Sinn ergibt: Wenn ich weiß, dass das Teilchen nicht “da” ist, dann sollte die Wahrscheinlichkeit, dass es “da” ist, gleich Null sein, sonst wäre unsere Physik ein bisschen unlogisch.
Und auch die Regel, dass die Summe über alle Quadrate der Wahrscheinlichkeitsamplituden gleich 1 ist, ergibt nun Sinn: Die Gesamtwahrscheinlichkeit, dass mein Teilchen in irgendeinem der möglichen Zustände ist, muss gleich 1 sein, denn irgendwas muss das Teilchen ja tun.
Das erklärt jetzt auch, warum man die Zustände nicht multiplizieren darf (so wie in der Aufgabe c oben), sondern addieren muss: Das Addieren von Zuständen spiegelt mathematisch die Tatsache wider, dass es sich um unterschiedliche Möglichkeiten handelt, die jeweils eine Wahrscheinlichkeit haben (bzw. eine Wahrscheinlichkeitsamplitude). Wenn ich mit einer Wahrscheinlichkeit von 10% drei richtige im Lotto habe und mit einer Wahrscheinlichkeit von 1% 4 richtige (die Zahhlen stimmen natürlich nicht), dann ist die Wahrscheinlichkeit für 3 oder 4 richtige eben 11%.
Die Wellenfunktion
Bisher konnte unser Teilchen nur an ganz bestimmten Orten sein – hier, da oder dort. Das ist natürlich nicht besonders realistisch – ein echtes Elektron kann sich ja so ziemlich überall rumtreiben, nicht bloß an ganz bestimmten Orten. Prinzipiell ändert das nichts an den Überlegungen, aber es macht die Schreibweise etwas komplizierter. Zu jedem möglichen Ort x gehört jetzt eine Wahrscheinlichkeitsamplitude – da es verdammt viele Orte x gibt, reicht das Alphabet nicht aus, um die ganzen Wahrscheinlichkeitsamplituden alle durchzubuchstabieren. Deswegen hat sich folgende einfache Schreibweise eingebürgert: Man schreibt die Amplitude (ich spare mir ab jetzt das volle Wort “Wahrscheinlichkeitsamplitude”, weil ich schreibfaul bin, jedenfalls dann, wenn die Sache eindeutig ist) für den Ort x, also für den Zustand |x>, einfach als ψ(x). Der Zustand des Teilchens ist dann also:
|Zustand> = ψ(x1) |x1> + ψ(x2) |x2>+ ψ(x3) |x3> + …
und zwar summiert über alle möglichen Werte von x.
 Mathematisch korrekt sind das unendlich viele Zustände, deswegen schreibt man das eigentlich besser als Integral, und das ψ(x)² ist eine Wahrscheinlichkeitsdichte. Spielt aber hier eigentlich keine Rolle.
Mathematisch korrekt sind das unendlich viele Zustände, deswegen schreibt man das eigentlich besser als Integral, und das ψ(x)² ist eine Wahrscheinlichkeitsdichte. Spielt aber hier eigentlich keine Rolle. 
In ψ(x) steckt jetzt also die Information darüber, mit welcher Wahrscheinlichkeit das Teilchen wo ist – die Wahrscheinlichkeit für den Ort x ist gegeben durch ψ(x)². Weil die Wellenfunktion einen Wert an jedem Punkt des Raumes hat, kann man sich das Hinschreiben der Ortszustände auch sparen und direkt sagen, dass ψ(x) den Zustand kennzeichnet. Manchmal wird die Schreibweise auch noch weiter verzerrt und man schreibt |ψ(x)> oder einfach nur |ψ> – das sieht ein bisschen komisch aus, aber da die Wellenfunktion den Zustand des Teilchens ja eindeutig kennzeichnet, kann man diese Schreibweise trotzdem so verwenden.
Als Beispiel betrachten wir ein Elektron, das wir auf einem Draht einsperren – es kann sich also nur in einer Richtung (der x-Richtung) bewegen und nicht in die anderen. Dann können wir ψ(x) einfach für verschiedene Fälle hinmalen. Dieses Bild (von Wikipedia, public domain) zeigt zwei mögliche Wellenfunktionen, links eine mit einer niedrigen, rechts eine mit einer hohen Energie. Die Darstellung der Kugel darunter soll symbolisieren, mit welcher Wahrscheinlichkeit wir das Teilchen an einem bestimmten Ort finden:
Im Zustand links ist das Elektron bevorzugt in der Mitte (da, wo die Wellenfunktion am größten ist), im Bild rechts hat sie mehrere Maxima und Minima.
Kleine Aufgabe: Warum ist im Bild rechts die Wahrscheinlichkeit, das Elektron am Ort eines der Minima zu finden, groß, obwohl der Wert der Wellenfunktion doch dort klein (weil negativ) ist?
Antwort: das liegt daran, dass die Wahrscheinlichkeit ja das Quadrat der Wellenfunktion ist, und beim Quadrieren fällt das negative Vorzeichen weg.
Wenn ihr mehr über diese speziellen Wellenfunktionen wissen wollt, könnt ihr das in meiner Schrödingergleichungs-Serie nachlesen.
Die Wellenfunktion ist – vor allem, wenn man Dinge wirklich ausrechnen will – ein wichtiger Bestandteil der Quantenmechanik. Für das grundlegende Verständnis von Dingen wie Quantenverschränkung oder Quantencomputern ist sie allerdings nicht so wichtig – diese Phänomene kann man auch an Systemen beobachten, bei denen wenige Zustände zur Beschreibung ausreichen (so wie unser Teilchen, das nur “hier” und “da” sein konnte).
So, und jetzt seid Ihr dran. Hat die Erklärung was genützt? Wisst Ihr mehr als vorher? Bräuchtet ihr noch mehr Beispiele oder kleine Mitdenk-Aufgaben?







Kommentare (197)