Das Wort “Nullpunktsenergie” geistert ja öfters mal herum – es ist eine Energie, die da ist, wenn eigentlich nichts da ist (nämlich im Vakuum), und manche Leute wollen sie sogar anzapfen und damit alle Energieprobleme der Welt lösen (das klappt aber nur in der science fiction). Das Konzept der Nullpunktsenergie stammt aber nicht aus der Theorie des Vakuums (oder der Elementarteilchen), sondern aus der Quantenmechanik von Atomen und Molekülen. Und zumindest dort hat diese Nullpunktsenergie auch ganz deutliche und messbare Konsequenzen.
Stellt euch ein einfaches Molekül vor, das aus zwei Atomen besteht, zum Beispiel ein Wasserstoff-Molekül. Das besteht ja aus zwei Wasserstoffatomen, die chemisch aneinander gebunden sind. Der Abstand zwischen den beiden Atomen in unserem Molekül ist durch die Kraft bestimmt: zum einen ziehen sie sich an, zum anderen möchten sie sich auch nicht zu nahe kommen, weil die Elektronen sich am liebsten über einen Bereich verteilen wollen (und weil die positiv geladenen Atomkerne sich abstoßen). (Relativ ausführlich habe ich das als Beispiel mal in der Quantenmechanik-verstehen-Serie besprochen.) Schiebt man die beiden Atome also dichter zusammen, dann stoßen sie sich ab, zieht man sie auseinander, dann ziehen sie sich an.
Zeichnet man die Energie als Funktion des Abstands, sieht das Bild etwa so aus:
Dabei habe ich in blau die Verteilung der Elektronenwolken (das Orbital) im Molekül eingezeichnet. Ihr seht, dass es einen Abstand gibt, bei dem die Energie minimal wird, das ist entsprechend der Gleichgewichtsabstand der Moleküle.
Wir können uns das – als brauchbare Analogie – so vorstellen, als wären die beiden Atome mit einer kleinen Feder verbunden, die gerade die passende Gleichgewichts-Länge hat. (Das ist natürlich nur eine Veranschaulichung, sooo kleine Federn gibt es nicht- die müssten dann ja auch aus Sub-Atomen bestehen, die sich anziehen, wofür wir dann Sub-Sub-Atome bräuchten usw….)
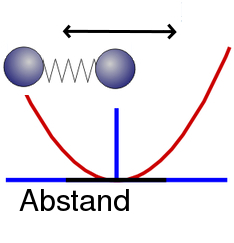
Im einfachsten Fall ist die rückstellende Kraft bei so einer Feder genau proportional zur Auslenkung: Je weiter ihr die Feder dehnt (oder staucht), desto größer wird sie. Schaut man sich die Energie an, die man reinstecken muss, um die Feder zu dehnen (oder zu stauchen, ich schreibe das jetzt nicht jedesmal mit hin…), so ist diese proportional zum Quadrat der Auslenkung, denn es gilt ja: Arbeit ist Kraft mal Weg, und wenn die Kraft porportional zum Weg ist, dann ist die Arbeit proportional zum Quadrat des Weges. Trägt man also die Energie auf, dann sieht das so aus:
Der blaue Strich kennzeichnet die Gleichgewichtslage, da wo die Atome in Ruhe sind und ihren energetisch günstigsten Abstand haben, die rote Linie zeigt, wie sich die Energie mit zunehmender Auslenkung ändert. Wenn ihr das Bild mit dem Bild für die Energie des Wasserstoffmoleküls oben vergleicht, dann seht ihr, dass die rote Parabel in der Nähe des Minimums eine ganz brauchbare Näherung darstellt. (Was mathematisch nicht verwunderlich ist, weil man so ziemlich jede Funktion in der Nähe des Minimums mit einer Parabel annähern kann.)
Wir haben also – in unserem einfachen Modell – zwei Objekte, die mit einer Feder verbunden sind. Wenn man die beiden Atome etwas auseinander zieht und dann loslässt, dann werden sie anfangen zu schwingen, jedenfalls nach den Regeln der klassischen Physik. Die Schwingung hat dabei eine bestimmte Frequenz (die Eigenfrequenz oder auch Resonanzfrequenz), die also sagt, wie lange eine Schwingung dauert. Solange die Auslenkung der Atome einigermaßen klein ist, ist die Frequenz unabhängig von der Auslenkung, und ihr könnt – immer noch im Rahmen der klassischen Physik – beliebige Auslenkungen bekommen. Die zugehörige Energie ist dadurch bestimmt, wie weit die beiden Atome maximal auseinander sind – auch sie kann entsprechend beliebige Werte annehmen.
Wir betrachten jetzt dieses System (zwei verbundene schwingende Atome, bei denen die Kraft dem einfachen Gesetz Kraft proportional zur Auslenkung folgt) mit den Regeln der Quantenmechanik. Die ganze Rechnerei überlassen wir den armen Physik-Studis, die hier ihre Fähigkeiten im Lösen partieller Differentialgleichungen üben können, hier geht es nur um das, was dabei herauskommt. (Ein didaktisches Problem in der Physik ist genau diese Trennung: In Physikvorlesungen und Büchern wird immer beides parallel gemacht: das Lösen fieser Gleichungen und ähnliches rein mathematisches Zeugs und das physikalische Argumentieren und Interpretieren vermischen sich da oft zu einem wirren und verwirrenden Brei, jedenfalls ging es mir und vielen meiner KommilitonInnen seinerzeit so.)







Kommentare (34)