Dieser Artikel gehört zu meiner Serie “Tatort-Wissenschaft”. Wer damit nichts anfangen kann findet hier eine Erklärung. Es geht in diesem Artikel nicht um eine wissenschaftliche Erklärung der Tatort-Handlung sondern darum zu zeigen, dass Wissenschaft tatsächlich überall ist. Egal was wir (oder die Tatort-Kommissare) machen, es steckt Wissenschaft dahinter. Wir erleben die Welt aber meistens getrennt. Da gibt es “Wissenschaft” – und dann gibt es “alles andere”. Zum Beispiel Krimis wie den Tatort. Es mag konstruiert erscheinen, den Tatort mit wissenschaftlichen Phänomenen und Erklärungen in Verbindung zu bringen. Die Wissenschaft war aber schon die ganze Zeit da. Unsere gedankliche Trennung zwischen Krimi und Wissenschaft ist konstruiert. Ach ja, und wenn ihr nicht wissen wollt, wer der Mörder war, dann lest am besten nicht bis zum Ende…
————————————————————————————————————————
Tatort-Folge Nummer 884 spielt in München. Es geht um Häuser und Baustellen. Es geht um Vergangenheit und Veränderung. Es geht um Dinge die immer gleich bleiben und es geht um eines der wichtigsten Theoreme der Physik.
Schon der Vorspann des Münchner Tatorts (der nach dem normalen Vorspann – der auch mal aktualisiert werden könnte! – kommt) zeigt, dass wir wieder mit dem Auftreten von “Kunst” rechnen müssen. Schnelle Schnitte, Rückblenden, Vorschau und jede Menge Protagonisten. Alles irgendwie sehr durcheinander und ohne Zusammenhang. Und das war eben nur der Vorspann! Der echte Tatort war noch viel verwirrender…
Die Kommissare Batic und Leitmayr haben es diesmal mit Baustellen zu tun. In ganz München wird gebaut und alte Stadtviertel werden in moderne Wohnsiedlungen für betuchte Menschen umgewandelt. Das nervt natürlich die eigentlichen Anrainer, die nicht nur mit jeder Menge Baulärm leben müssen, sondern sich bald die Mieten in ihrem eigenen Viertel nicht mehr leisten können. Und das nervt auch Kommissar Leitmayr der kurzfristig in eben so einem Baustellenviertel wohnt weil seine eigene Wohnung anscheinend einen Wasserschaden hat. Der Weg dorthin wird ihm aber von einer Baustelle nach der anderen versperrt und das Navigationsgerät in seinem Auto lotst ihn im Kreis herum und von Stau zu Stau aber nicht dorthin, wo er hin will. Er ist in gewissem Sinn gleich doppeltes Opfer einer Invarianz geworden.
Als “Invarianz” beziehungsweise “Invariante” bezeichnet man in der Physik eine Größe, die sich unter einer bestimmten Transformation nicht verändert. Ich kann zum Beispiel eine 10-Kilo-Hantel nehmen und sie einmal von vorne betrachten und dann um sie herum gehen und sie von hinten ansehen. Ihr Gewicht wird sich dadurch nicht ändern; es ist invariant. Das ist ein bisschen so wie mit den Baustellen in München die Leitmayr auf die Nerven gehen. Da werden Politiker bestochen und falsche Gutachten erstellt, damit alte Häuser abgerissen werden können. Aber dort wo die alten Häuser gestanden sind stehen danach bald wieder neue Häuser und im großen und ganzen hat sich nichts geändert…
Emmy Noether musste ohne Gehalt an der Uni arbeiten weil Mathematik nichts für Frauen ist…
In der Physik sind solche Invarianzen von großer Bedeutung und es gibt ein sehr berühmtes Theorem, dass sich mit ihnen beschäftigt. Es wurde 1918 von der Mathematikerin Emmy Noether formuliert und trägt deswegen auch den Namen “Noether-Theorem”. Man kann es eigentlich recht knapp und prägnant formulieren:
“Zu jeder kontinuierlichen Symmetrie eines physikalischen Systems gehört eine Erhaltungsgröße.”
Hinter diesem simplen Satz steckt allerdings jede Menge fundamentale Physik! Eine “kontinuierliche Symmetrie” ist eine Transformation, bei der konkrete Anfangsbedingungen keine Rolle spielen. Eine Quadrat zum Beispiel kann ich um 90 Grad drehen und es sieht danach wieder genau so aus wie vorher. Es ist symmetrisch gegenüber einer Rotation von 90 Grad (oder 180 Grad oder 270 Grad). Aber nicht gegenüber einer Rotation von zum Beispiel 37 Grad – danach würde das Quadrat deutlich schief liegen und nicht mehr so wie vorher aussehen. Es ist keine kontinuierliche Symmetrie. Einen Kreis dagegen kann ich drehen so viel ich will. Egal um welchen Winkel ich ihn drehe, er sieht danach genau so aus wie vorher. Das ist eine kontinuierliche Symmetrie und die sind es, die im Noether-Theorem von Bedeutung sind.
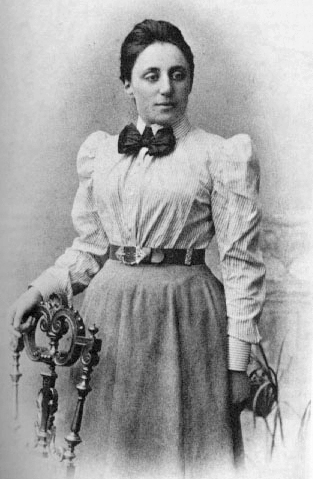
Kommentare (32)