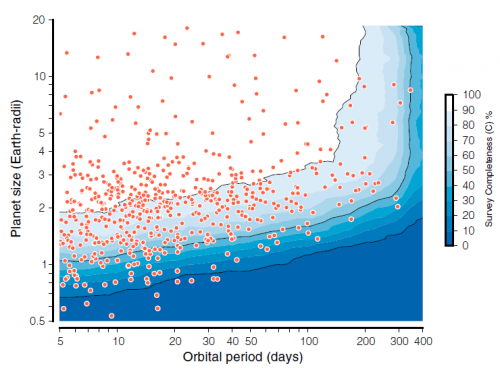
Das Diagramm zeigt auf der x-Achse die Umlaufzeit der Planeten in Tage und auf der y-Achse die Größe der Planeten in Erdradien. Die Farben im Diagramm geben an, wie komplett die Daten von Kepler sind. Denn Kepler findet ja nicht alles: Das Teleskop kann nur die Planeten entdecken, die von der Erde aus gesehen genau vor dem Stern vorüber ziehen. Sind ihre Bahnen zu stark gegenüber unserer Sichtlinie geneigt, dann sieht man nichts. Und die Ausrichtung anderer Planetensystem ist willkürlich; ohne System. Wir verpassen also jede Menge Planeten, die zwar da sind, aber halt leider von uns aus gesehen nicht an ihrem Stern vorüber ziehen. Außerdem verpassen wir viele Planeten die Sterne umkreisen die zu schwach leuchten; Planeten die zu klein sind und übersehen werden und Planeten, die zu lange für eine Umrundung ihres Sterns brauchen und die wir deswegen noch nicht beobachten konnten. Diese Faktoren kann man aber alle recht gut abschätzen und genau das haben Petigura und seine Kollegen gemacht. Dort wo das Diagramm weiß ist, wissen wir zum Beispiel, dass wir alles entdeckt haben. Alle Planeten die in diesen Bereich fallen, müssen ein Signal erzeugen, dass stark genug ist um von Kepler gesehen zu werden. Aber je kleiner die Planeten werden bzw. je weiter sie vom Stern entfernt sind, desto schwerer sind sie zu beobachten und desto weniger komplett sind die Daten (und um so blauer das Diagramm).
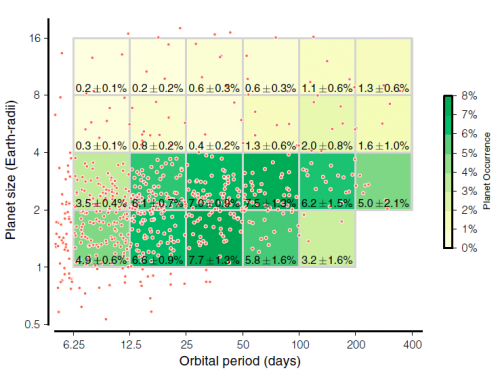
Im nächsten Schritt haben Petigura und seine Kollegen die Planeten in Gruppen eingeteilt und nachgesehen, wie viele Sterne Planeten mit bestimmten Eigenschaften haben:
Das Diagramm ist identisch mit dem vorherigen. Die Achsen zeigen die gleichen Größen und die roten Punkte sind die gleichen 603 Planeten. Das Diagramm wurde aber in 30 Bereiche eingeteilt die bestimmten Kombinationen von Planetengröße und Umlaufzeit entsprechen. Und für jedes dieser Kästchen haben Petigura und seine Kollegen bestimmt, wie viele Sterne Planeten mit genau diesen Eigenschaften haben. Zum Beispiel haben 7,7 Prozent (plus/minus 1,3%) aller sonnenähnlichen Sterne Planeten mit Umlaufzeiten die zwischen 25 und 50 Tagen liegen und die 1 bis 2 Mal so groß wie die Erde sind (das dritte Kästchen von rechts in der vierten Reihe von oben aus gezählt). Kästchen wurden nur dann gezeichnet, wenn die Vollständigkeit der Daten mindestens über 25 Prozent liegt; deswegen gibt es ganz unten im Diagramm keine Zahlen.
So weit, so gut und so interessant. Solche Analysen sind äußerst interessant wenn man herausfinden will, wie vielfältig die Planeten tatsächlich sind. In den ersten Jahren der Suche nach extrasolaren Planeten fanden wir ja hauptsächlich sehr große Himmelskörper; alle ungefähr so groß wie Jupiter oder größer. Das war logisch, denn die sind am leichtesten zu finden. Aber es war eben nicht von Anfang an klar, ob das nur ein Auswahleffekt ist oder ob die großen Planeten wirklich häufig sind und kleine Planeten wie die Erde die Ausnahme. Dank solcher Analysen (die auch früher schon gemacht wurden) wissen wir nun, dass die Planeten um so häufiger werden, je kleiner sie sind. Große Planeten sind die Ausnahme und kleine Planeten wie die Erde die Regel.
Aber natürlich interessiert die meisten Menschen die Größe der Planeten nicht so sehr wie die Bedingungen dort. Wir wollen wissen wie viele erdgroße Planeten es gibt, die genau im richtigen Abstand zu ihrem Stern sind. Dort, wo es weder zu heiß noch zu kalt ist. Dort, wo theoretisch Leben existieren kann.
Das zu wissen wäre wirklich nett – nur leider ist in den Daten von Petigura und seinen Kollegen kaum etwas dazu zu finden. Man hat kaum Planeten gefunden, die im richtigen Abstand zu ihrem Stern sind. Das sind man ja auch in den beiden Diagrammen weiter oben: Die meisten Datenpunkte findet man im linken Bereich, also dort, wo die Umlauzeiten klein sind. Unsere Erde hat eine Umlaufzeit von 365 Tagen und so weit rechts im Diagramm gibt es kaum Daten. Denn je länger die Umlauzeit ist, desto länger muss man auch beobachten und Kepler hat noch nicht lange genug beobachtet um wirklich viele solcher Planeten zu finden (und wird das auch nicht mehr tun können weil das Teleskop mittlerweile defekt ist). Petigura und seine Kollegen mussten sich also einen anderen Weg überlegen und haben deswegen dieses Diagramm gezeichnet:











Kommentare (76)