 Dieser Artikel ist Teil einer fortlaufenden Besprechung des Buchs “Wenn Gott würfelt: oder Wie der Zufall unser Leben bestimmt” (im Original: “The Drunkard’s Walk: How Randomness Rules Our Lives”) von Leonard Mlodinow. Jeder Artikel dieser Serie beschäftigt sich mit einem anderen Kapitel des Buchs. Eine Übersicht über alle bisher erschienen Artikel findet man hier.
Dieser Artikel ist Teil einer fortlaufenden Besprechung des Buchs “Wenn Gott würfelt: oder Wie der Zufall unser Leben bestimmt” (im Original: “The Drunkard’s Walk: How Randomness Rules Our Lives”) von Leonard Mlodinow. Jeder Artikel dieser Serie beschäftigt sich mit einem anderen Kapitel des Buchs. Eine Übersicht über alle bisher erschienen Artikel findet man hier.
——————————————————-
Im ersten Kapitel des Buchs hat Mlodinow anschaulich dargelegt, wie sehr der Zufall unser Leben bestimmt und vor allem dort, wo wir nicht damit rechnen. Das zweite Kapitel hat sich mit den grundlegenden Regeln der Wahrscheinlichkeit beschäftigt. Im dritten Kapitel präsentiert Mlodinow das fiese Ziegenproblem, das unser Unverständnis der Wahrscheinlichkeit eindrucksvoll präsentiert. Das vierte Kapitel beschäftigt sich mit den Methoden zur Berechnung von Wahrscheinlichkeiten die vor allem Blaise Pascal im 17. Jahrhundert entwickelt hat. Das fünfte Kapitel beschäftigt sich mit der Frage, was Wahrscheinlichkeiten in der realen Welt eigentlich bedeuten. Kapitel 6 erklärt die verwirrende Bayesschen Wahrscheinlichkeiten die für unser Alltagsleben von großer Bedeutung sind.
In Kapitel 7 wechselt Leonard Mlodinow das Thema. Bis jetzt ging es immer um Wahrscheinlichkeitsrechnung. Nun taucht das erste Mal die Statistik auf. Die beiden Themen sind zwar verwandt, aber unterschiedlich. In der Wahrscheinlichkeitsrechnung kennt man die Wahrscheinlichkeiten, mit der bestimmte Ereignisse eintreten schon vorher und nutzt sie, um die Wahrscheinlichkeit für den Eintritt anderer Ereignisse zu berechnen. Aber in der Realität will man oft auch andere Probleme lösen. Zum Beispiel in der Wissenschaft: Da geht es meistens nicht darum, dass man den Wert einer bestimmten Messgröße kennt und die Wahrscheinlichkeit bestimmen will, mit der die Messungen diesen Wert erreichen. Da hat man jede Menge Messungen und will damit den konkreten Wert der Messgröße bestimmen. Und dafür braucht man die Statistik.
Man muss sich außerdem im klaren darüber sein, dass jede reale Messung ein zufälliges Element beinhaltet (und dabei rede ich jetzt nicht von der Quantenmechanik). Mlodinow bringt das Beispiel der Englischlehrerin seiner Tochter. Hausarbeiten werden dort auf einer Skala von 1 bis 100 beurteilt. Aber was bedeutet es wirklich, wenn eine Arbeit mit der Note “92” beurteilt wird und wie unterscheidet sich diese Arbeit von einer mit der Note “93”? Kann ein Lehrer wirklich objektiv so feine Unterscheidungen treffen? Studien zeigen, dass das nicht der Fall ist.
Lässt man unterschiedliche Lehrer die gleichen Arbeiten nach den gleichen Kriterien beurteilen, kommen sie trotzdem selten zum gleichen Ergebnis. Es spielen eben zu viele zufällige Faktoren eine Rolle. Genau so wie bei anderen subjektiven Beurteilungen, zum Beispiel dem Geschmack von Wein. Auch hier zeigen Studien regelmäßig, dass auch Experten nicht in der Lage sind, konsistente Beurteilungen abzugeben. Zu viele zufällige und psychologische Faktoren spielen Rolle. Weine, von denen man erwartet dass sie gut schmecken, werden besser beurteilt als sie beurteilt werden wenn die Tester vorher der Meinung sind sie würden schlecht schmecken. Zwei identische Weißweine werden unterschiedlich beurteilt wenn einer davon mit einem geschmack- und geruchlosen Farbstoff rot gefärbt wird und selbst wenn es nur daraus geht aus drei Weinen die beiden herauszuschmecken die identisch sind, sind die Experten nicht in der Lage, das zuverlässig zu tun. Und das gilt natürlich nicht nur für Wein: In Tests scheitern die Menschen auch regelmäßig daran, Coca Cola von Pepsi Cola zu unterscheiden, selbst wenn sie davon überzeugt sind, die eine Marke zu mögen und die andere nicht.
Wenn also 15 Weinexperten einem Wein (auf einer Skala von 1 bis 100) die Noten 80, 81, 82, 87, 89, 89, 90, 90, 90, 91, 91, 94, 97, 99 und 100 geben: Was hat das dann zu bedeuten? Und wie unterscheidet sich so ein Urteil von 15 Experten die dem Wein alle eine Note von 90 Punkten geben? Berechnet man den Durchschnitt der Noten, erhält man jedesmal 90 Punkte. Aber ganz offensichtlich unterscheidet sich der eine Fall vom anderen. In der ersten Serie gibt es viel mehr Variation und die wird mit der Standardabweichung beschrieben. Sie beträgt in diesem Fall 6 Punkte und alles was man über diesen Wein sagen kann ist, dass er eine Note hat, die irgendwo zwischen 84 und 96 liegt.
Die Standardabweichung von Daten wird oft vernachlässigt und es wird ignoriert, dass Variationen einer Größe innerhalb der Standardabweichung keine Bedeutung haben. Wenn zum Beispiel bei einer Meinungsumfrage herauskommt, dass die Zustimmung zur Politik der SPD von 30 auf 34 Prozent gestiegen ist, dann wird das die SPD sicherlich freuen und vermutlich wird die PR-Abteilung entsprechende Pressemitteilungen verfassen die erklären, dass die Bevölkerung die Arbeit der Partei würdigt, man auf dem richtigen Weg ist, und so weiter. Aber solange man die Standardabweichung nicht kennt, macht das alles keinen Sinn. Sagen wir, sie beträgt bei dieser Umfrage 5 Prozent. Das bedeutet folgendes: Würde man die Umfrage unmittelbar wiederholen, dann kann der Zustimmungswert dieses Mal auch bei 29 Prozent landen weil die SPD-Anhänger gerade alle am Klo waren und nicht ans Telefon gegangen sind. Oder aber man kriegt einen Wert von 39 Prozent. Wenn sich eine Messgröße um 4% ändert, die Standardabweichung aber 5% beträgt, dann ist die Änderung ohne Bedeutung weil es sich genau so gut um eine zufällige Fluktuation handeln kann.
Bei jeder realen Messung macht man Fehler und die hängen normalerweise vom Zufall ab. Die ersten, die sich intensiv damit auseinandersetzen mussten, waren die Astronomen im 17. und 18. Jahrhundert. Ausgerüstet mit Newtons Gravitationstheorie wollten sie die Bewegung der Himmelskörper berechnen und mussten dazu die Daten von Beobachtungen auswerten. Was ein Astronom misst, hängt von dem Gerät ab, das er benutzt, von den Unruhen in der Luft, von den Temperaturschwankungen, der Adaption der Augen an die Dunkelheit, der Stimmung des Astronom und jeder Menge anderer zufälliger Faktoren. Die Messwerte waren also nie identisch sondern variierten um einen Wert herum. Die Frage war nun: Wie genau sind die Messfehler verteilt?
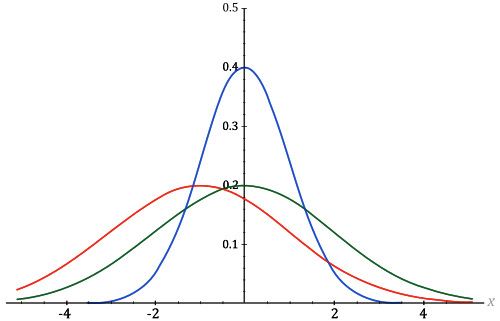
Das entsprechende mathematische Gesetz dass die Verteilung von Messfehlern bestimmt wird heute Normalverteilung oder Gaußverteilung genannt (nach Carl Friedrich Gauß, der es formuliert hat – obwohl vor ihm auch andere Wissenschaftler schon ähnliche Ideen hatten). Der Form der Verteilung nach wird sie auch “Glockenkurve” genannt:
Wiederholt man eine Messung immer wieder und erstellt ein Diagramm, das anzeigt wie oft man einen bestimmten Wert erhalten hat, dann bekommt eine Kurve, die so aussieht wie in obigem Bild. Die meisten Messungen werden sich um einen Maximalwert herum verteilen; man wird aber auch immer wieder vereinzelte Messungen erhalten, die stark von diesem Wert abweichen. Die Kurve kann breit sein oder schmal und natürlich wird der Maximalwert je nach Art des gemessenen Phänomens ein anderer sein. Aber die grundlegende Form ist immer gleich und sie kann immer mit der gleichen mathematischen Formel beschrieben werden.
Diese Formel erklärt auch, wie die Standardabweichung zu interpretieren ist: Je stärker die einzelnen Messwerte varieren, desto breiter ist die Kurve. Folgen Messwerte einer Gaußverteilung, dann werden immer 68,27% der Messungen in einem Bereich von genau einer Standardabweichung landen. Würde man zum Beispiel 10.000 Weinexperten einen Wein testen lassen und ihre Noten aufzeichnen, würde man eine Glockenkurve erhalten. Sagen wir, der Maximalwert der Kurve liegt bei 56 Punkten und die Standardabweichung beträgt 5 Punkte. Dann haben 6827 Tester dem Wein eine Note gegeben, die zwischen 51 und 61 Punkten beträgt. 95,45% der Messungen liegen bei einer Glockenkurve im Bereich von zwei Standardabweichung. 9545 der Tester haben den Wein also mit einer Note zwischen 46 und 66 Punkten bewertet. 99,73 der Datenpunkte liegen im Bereich von drei Standardabweichung: 9973 Tester haben dem Wein zwischen 41 und 71 Punkte gegeben. Und so weiter.
Die Gaußverteilung erlaubt es, genau diese Zusammenhänge exakt zu berechnen. Führt man ein Experiment wiederholt durch, dann werden die zufälligen Fehler dafür sorgen, dass sich die Ergebnisse nach der Glockenkurve verteilen (das gilt aber nicht für systematische Fehler!). Eine genau Analyse ermöglicht es dann herauszufinden, wie exakt man mit diesen Messungen den tatsächlichen Wert bestimmt hat. Sie sagt uns aber auch, dass wir sehr gut aufpassen müssen, wenn wir nur wenige oder gar nur einen Datenpunkt zur Verfügung haben. Denn die Glockenkurve hat links und rechts kein Ende. Es wird zwar immer unwahrscheinlicher, dass ein einzelner Messwert extrem stark vom Mittelwert abweicht. Aber es gibt diese Abweichungen und wenn man nur eine einzige Messung macht kann man nicht sicher sein, dass man nicht gerade zufällig einen Extremwert gemessen hat, der vom tatsächlich Wert vollkommen abweicht.
Und das gilt um so mehr, wenn die ganze Sache chaotisch wird. Aber das passiert erst im nächsten Kapitel.












Kommentare (41)