Dieser Gastartikel ist ein Beitrag zum ScienceBlogs Blog-Schreibwettbewerb. Alle eingereichten Beiträge werden im Lauf des Septembers hier im Blog vorgestellt. Danach werden sie von einer Jury bewertet. Aber auch alle Leserinnen und Leser können mitmachen. Wie ihr eure Wertung abgeben könnt, erfahrt ihr hier.
Dieser Beitrag wurde von Martin Neukamm eingereicht.
———————————————————————————————————————–
Die radiometrische Datierung ist eine etablierte Methode der Altersbestimmung,
sozusagen der „Goldstandard“ zur Messung archäologischer, erdgeschichtlicher
und kosmischer Zeiträume. Alle darauf basierenden Methoden nutzen das Wis-
sen, dass instabile (radioaktive) Atomkerne im Laufe der Zeit zerfallen und sich
dabei in andere Atomkerne umwandeln. Der Zeitraum, in dem statistisch genau
50 Prozent der Vertreter einer bestimmten Sorte von Atomkernen zerfallen,
nennt man Halbwertszeit. Die Halbwertszeiten der meisten radioaktiven Elemen-
te sind heute sehr genau bekannt. Das Uran-238 [1] beispielsweise hat eine Halb-
wertszeit von 4,47 Milliarden Jahren. Das bedeutet, dass sich innerhalb dieses
Zeitraums genau die Hälfte der ursprünglich vorhandenen Stoffmenge an Uran-
238 („Mutter-Nuklid“) in das Element Thorium-234 („Tochter-Nuklid“) umwan-
delt. Dieses ist selbst radioaktiv und verwandelt sich innerhalb von 24 Tagen zur
Hälfte in das Element Protactinium-234, welches noch rascher zerfällt. Am Ende
dieser so genannten Zerfallsreihe steht das stabile Blei-206. Man kann also ver-
einfacht sagen, dass sich die Hälfte der Menge des Elements Uran-238 innerhalb
von 4,47 Milliarden Jahren in das Element Blei-206 verwandelt.
Um etwa das Alter einer Gesteinsschicht zu datieren, braucht man im einfachsten
Fall nur die Menge von Uran-238 sowie die Menge von Blei-206 in den Gesteins-
mineralien zu bestimmen und kann ermitteln, wieviel Prozent der ursprünglich
vorhandenen Atomkerne des Uran-238 zerfallen sind. Nach untenstehender For-
mel (Abb. 1) lässt sich das Alter des Gesteins bzw. Minerals errechnen. (In
Wahrheit ist die Bestimmung etwas komplizierter, auf die Details brauchen wir
hier nicht einzugehen.)
Abb. 1: Formel zur Berechnung des Alters einer Mineralienprobe. „Pjetzt“ ist die Stoffmen-
ge des radioaktiven „Mutter-Nuklids“ (z. B. Uran-238) und „Djetzt“ die Stoffmenge des
stabilen „Tochter-Nuklids“ (z. B. Blei-206) in der zu datierenden Probe. Hat man die
Stoffmenge beider Nuklide bestimmt, lässt sich über die Halbwertszeit das Alter errech-
nen. Quelle: www.waschke.de/twaschke/artikel/isochron/isochr_1.htm
Nun gibt es immer wieder Leute, die die Zuverlässigkeit dieser etablierten
Methode anzweifeln – seien es nun Kreationisten, die glauben, Erde und Kosmos seien nur
wenige Tausend Jahre alt, Chronologiekritiker, die meinen, im Mittelalter seien mehrere
Jahrhunderte schlichtweg erfunden worden, die es in Wirklichkeit nie gab, oder Hobbyphi-
losophen, die behaupten, historische Theorien hätten keinen naturwissenschaftlichen Status,
da sie nicht überprüfbare philosophische Annahmen enthielten.
Eine dieser „philosophischen Annahmen“ ist das so genannte Aktualitätsprinzip,
welches davon ausgeht, dass sich die Naturkonstanten, die wir heute im Labor
bestimmen können, wie etwa die Halbwertszeiten radioaktiver Nuklide, auch im
Laufe von Jahrmilliarden nie verändert haben. Diese Annahme, so liest man bei-
spielsweise bei BRESTOWSKY (2009), sei eine metaphysische Grundannahme, die
sich nicht empirisch belegen lasse. Deshalb könne man, so KOTULLA (2014) über
die Zuverlässigkeit radiometrische Altersbestimmungen keine sicheren Aussagen
treffen; eine davon unabhängige Methode zur Absicherung erdgeschichtlicher
Zeiträume gäbe es auch nicht.
Wir wollen im vorliegenden Beitrag diese Kritik zum Anlass nehmen, zu untersu-
chen, ob die These, Halbwertszeiten seien variabel, wissenschaftlich vertretbar
ist und wie zuverlässig radiometrische Methoden tatsächlich sind. Wir werden
auch sehen, ob es tatsächlich keine Möglichkeit gibt, radiometrische Altersbe-
stimmungen unabhängig vom radioaktiven Zerfall zu überprüfen.
Variable Halbwertszeiten und bewohnbare Universen
Die Behauptung, die Konstanz der Halbwertszeiten radioaktiver Nuklide sei nicht
erwiesen, ist aus verschiedenen Gründen ein sehr schwaches Argument. Was die
Kritiker geflissentlich übergehen: Wären die Halbwertszeiten früher nennenswert
verschieden von den heutigen Werten gewesen, hätten sich auch die Verhältnisse
der vier Grundkräfte der Physik zueinander fundamental verändert. Die Halb-
wertszeit eines „Alpha-Strahlers“ wie Uran-238 beispielsweise hängt vom Ver-
hältnis der starken Kernkraft zur so genannten Coulomb-Wechselwirkung (elekt-
romagnetischen Abstoßung) der Protonen im Kern ab. Eine nennenswerte Ver-
kürzung der Halbwertszeit – ein erforderlicher Schritt, um die geologische Zeit-
messung mit den Annahmen des Kreationismus in Einklang zu bringen – würde
entweder eine Verringerung der starken Kernkraft oder eine Erhöhung der elekt-
romagnetischen Abstoßung voraussetzen.
Wäre aber die starke Wechselwirkung nur um wenige Prozent schwächer, wäre
Wasserstoff das einzige Element im Universum (MCGRATH 2001, 217). Schwerere
Elemente wären instabil, Sterne (typische Fusionsreaktoren) hätten sich nie ge-
bildet. Wäre dagegen die elektromagnetische Kraft nur ein klein wenig stärker,
wäre der gesamte Wasserstoff im Universum innerhalb weniger Jahre in Helium
umgewandelt worden – langlebige Sterne wie die Sonne könnten nicht existieren.
In den meisten Fällen also würden Schwankungen der Halbwertszeiten
um bereits wenige Prozent zu einem instabilen, lebensfeindlichen Kos-
mos führen; analoge Überlegungen lassen sich auch für andere Formen des ra-
dioaktiven Zerfalls wie den „Beta-Zerfall“ anstellen.
Gemessen an elementaren Zusammenhängen der Physik gibt es also keinen
Spielraum für eine deutliche Veränderung der Halbwertszeiten radioaktiver Nuk-
lide. Eine „isolierte“ Erhöhung oder Erniedrigung der Zerfallskonstanten ist kaum
möglich, ohne das filigrane Netz der Naturgesetze und -Konstanten in fataler
Weise aus der Balance zu bringen. Es gibt nur eine Zerfallsart, auf die das nicht
zutrifft, nämlich den Zerfall über Elektroneneinfang (electron capture).
Eine Ausnahme: Der Mechanismus des electron capture
Beim Elektroneneinfang wird ein Elektron aus der Atomhülle vom Atomkern auf-
genommen, sodass sich ein Proton in ein Neutron und ein Neutrino verwandelt.
Diese Halbwertszeit kann sich dramatisch ändern, wenn Elektronen aus der Hülle
entfernt werden. Man denke an das extreme Beispiel, dass alle Elektronen aus
der Hülle entfernt wurden. In diesem Fall liegt ein „nackter“ Atomkern vor. Die-
ser kann nicht mehr über Elektroneneinfang zerfallen, da kein Hüllenelektron
mehr vorliegt. Die Halbwertszeit wird unendlich und der Kern stabil. Dieses Phä-
nomen wurde experimentell an der GSI 1996 in einem Speicherringexperiment
beobachtet (vgl. BOSCH et al.1996). Diese Zerfallsart ermöglicht sogar eine von
anderen radiometrischen Datierungsmethoden unabhängige Altersbestimmung
des Universums; eine Vertiefung dieses Themas würde allerdings den Rahmen
unserer Betrachtungen sprengen.
Wenn Ozeane verdampfen
Aber nehmen wir spaßeshalber einmal an, dass die Halbwertszeiten radioaktiver
Nuklide früher um mehrere Größenordnungen niedriger lagen als heute. Welche
Auswirkungen hätte dies auf die Erde gehabt? Man kann sich leicht ausrechnen,
um welchen Faktor die bei radioaktiven Zerfällen freiwerdende Energie (Bin-
dungsenergie der Nukleonen) höher sein müsste, um die Ergebnisse der Zeit-
messung beispielsweise mit den Behauptungen der Kreationisten zu harmonisie-
ren, die Erde sei erst ein paar Tausend Jahre alt: Da sich das Erdalter auf rund
4,56 Milliarden Jahre datieren lässt, wäre eine Verkürzung der Halbwertszeit um
rund sechs Zehnerpotenzen (Faktor eine Million) erforderlich. Auch die Zerfalls-
leistung (Energie pro Zeit) würde um diesen riesigen Faktor anwachsen.
Knapp die Hälfte der Erdwärme stammt heute aus dem Zerfall radioaktiver Ele-
mente. Die Leistung, die aus dem radioaktiven Zerfall resultiert, beträgt rund
2·1013 Watt, also 20 Terawatt (GANDO et al. 2011). Einen Erdradius von 6.370 km
zugrunde gelegt, liegt die geothermische Leistungsdichte des radioaktiven Zer-
falls bei etwa 0,040 Watt (40 mW) pro Quadratmeter Erdoberfläche. Eine um
sechs Größenordnungen höhere Zerfallsleistung entspräche demnach einer Wär-
meleistung von 40.000 W (40 kW) pro Quadratmeter Erdoberfläche.
Wenn man sich vergegenwärtigt, dass dieser Wert ziemlich genau der Leistungs-
dichte einer modernen Ceranfeld- oder Herdplatte entspricht, kann man sich
leicht ausmalen, was passieren würde: Die Ozeane würden innerhalb kürzester
Zeit zu kochen beginnen und verdampfen. Anschließend würde sich die Erde all-
mählich bis zur Weißglut erhitzen und lange davor jede Lebensform vernichtet
haben. Jeden Wassers beraubt, das die enorme Hitze aus dem Erdinneren auf-
nehmen könnte, würde die Erde schließlich selbst verdampfen (ROGNSTAD 2005).
Kurzum: Der Versuch, radiometrische Datierungen durch willkürliche An-
nahmen auf ein „biblisches Alter“ herunter zu korrigieren, liegt wissen-
schaftlich gesehen nicht annähernd im Bereich des Möglichen – zumin-
dest, solange die Gesetze der Physik Gültigkeit haben.
Mitte des 20. Jahrhunderts gab es ähnliche Überlegungen seitens des Physikers
und Nobelpreisträgers Paul DIRAC. Er opferte die Konstanz elementarer Naturge-
setze, etwa der Gravitationskonstante. Seine Hypothese hatte nicht lange Be-
stand, denn Berechnungen zeigten ebenfalls, dass unter seinen Annahmen die
Ozeane hätten verkochen müssen (BARROW 2011, 106). Unter der Titelzeile
„DIRAC lässt Ozeane kochen“ spitzten diverse Medien das Problem polemisch zu.
Danach wurde die Idee verworfen. Sie erinnert an das Bestreben des Kreationis-
mus, an Zerfallskonstanten beliebig herum zu manipulieren, bis die Geologie „zur
Bibel passt“. „Kreationisten bringen die Meere zum Kochen“ wäre auch hier der
passende Slogan.
DIRAC zog die Lehren aus seinem Irrtum, der Kreationismus jedoch hat immer
den weltanschaulichen Joker des TERTULLIAN parat: „Credo, quia absurdum est!“
„Ich glaube, weil es unvernünftig ist!“ Und je absurder eine Annahme, desto fes-
ter, so scheint es, glaubt der Kreationismus.
Naturreaktoren, Meteoriten und Quasare belegen die Konstanz der Halb-
wertszeiten
Was den Kritikern ebenfalls entgangen zu sein scheint, ist die Tatsache, dass die
Frage nach der Konstanz der Halbwertszeiten seit Jahren intensiv erforscht
wird. Da bestimmte Formulierungen der String-Theorie innerhalb gewisser Gren-
zen veränderliche Naturkonstanten nahe legen, wurde nach Möglichkeiten ge-
sucht zu prüfen, ob dem tatsächlich so ist.
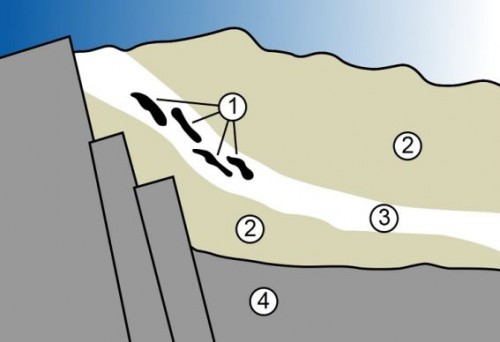
Eine Möglichkeit zur Beobachtung bot der Naturreaktor von Oklo (Abb. 2). Dabei
handelt es sich um einen natürlich entstandenen Kernreaktor, der in einer frühen
Ära der Erdgeschichte aktiv war. Im heutigen Gabun enthielt das Flusswasser des
Oklo große Mengen löslicher Uran-Komplexe, die in der schlammigen Uferzone zu
unlöslichen Verbindungen reduziert wurden. Im Mündungsdelta des Flusses la-
gerten sich so große Mengen Uran ab, dass die kritische Masse, bei der eine Ket-
tenreaktion einsetzen kann, überschritten wurde. In umliegendes Sandgestein
eindringendes Wasser bremste die Neutronen auf die für eine Kettenreaktion er-
forderliche Geschwindigkeit ab und „schaltete“ so den Reaktor an. Das Wasser
verdampfte und sickerte anschließend wieder in das trockene Gestein ein. So
wurde der Reaktor über mehrere Hunderttausend Jahre hinweg zyklisch an- und
wieder abgeschaltet. Man entdeckte den Naturreaktor, nachdem festgestellt wur-
de, dass die Lagerstätte gegenüber den übrigen sich auf der Welt befindlichen
Uranlagerstätten einen signifikant niedrigeren Gehalt an Uran-235 aufweist.
Um zu prüfen, ob sich die Halbwertszeiten im Lauf der Erdgeschichte verändert
haben, braucht man nur die relativen Konzentrationen der verschiedenen Isotope
in Oklo zu bestimmen und mit heutigen Isotopenverhältnismessungen zu verglei-
chen. Beispielsweise können Kerne des Elements Samarium-149 Neutronen ein-
fangen, die bei der Spaltung von Uran-235 freigesetzt werden, und werden
dadurch zum Isotop Samarium-150 (BOWLES 2004). Das Mengenverhältnis dieser
und anderer Isotope zueinander wird von der Geschwindigkeit des Neutronenein-
fangs sowie von den Halbwertszeiten der Nuklide bestimmt. Wären die Halb-
wertszeiten langlebiger Nuklide früher anders gewesen, hätte man in Oklo-
Proben dramatisch andere Isotopenverhältnisse vorfinden müssen als erwartet.
Dem ist aber nicht so. Im Gegenteil, die Reaktionsprodukte längerer Halbwerts-
zeit existieren in genau jenem Isotopenverhältnis, wie man es von einem Kern-
reaktor mit verbrauchtem Brennstoff erwarten würde. Zerfallsprodukte mit kur-
zer Halbwertszeit fehlen im umliegenden Gestein, was zeigt, dass der Reaktor
vor 1,7 Milliarden Jahren endgültig „abgeschaltet“ wurde. Isotopenverhältnis-
messungen an Meteoriten bestätigen die Konstanz der Halbwertszeiten ebenfalls.
Abb. 2: Geologische Voraussetzungen des Naturreaktors in der Oklo-Mine: (1): Reaktor-
zonen, (2): Sandstein, (3): Erzflöz, (4): Granitstock. Bild: © MesserWoland – Wikipedia
(https://de.wikipedia.org/wiki/Naturreaktor_Oklo. Lizenz: CC-BY-SA-2.5,
www.creativecommons.org/licenses/by-sa/2.5/deed.de
Es gibt weitere Möglichkeiten nachzuweisen, dass die Halbwertszeiten auf einem
Niveau von etwa 10-16 bis 10-18 ihres Werts konstant geblieben sind. Dazu zählt
die Beobachtung der Spektren sehr weit entfernter und somit auch sehr alter Ga-
laxien. Die Absorptionslinien so genannter Quasare (Abb. 3) entsprechen jenen,
die wir auch im Labor messen können. Die Übergänge hängen empfindlich vom
Wert der so genannten SOMMERFELD‘schen Feinstrukturkonstante Alpha ab, wel-
che die Stärke der elektromagnetischen Wechselwirkung angibt. Wie oben be-
sprochen, beeinflusst die Stärke der elektromagnetischen Wechselwirkung auch
die Halbwertszeiten radioaktiver Nuklide. Da die Spektren keine nennenswerten
Unterschiede zeigen, sind auch die Halbwertszeiten auf hohem Niveau konstant
geblieben. Die Invarianz der Feinstrukturkonstante beweist auch die Konstanz
weiterer Naturkonstanten, wie etwa der Lichtgeschwindigkeit.
Abb. 3: Zwei Quasare in Falschfarben-Darstellung. Als Quasare (quasi-stellare Objekte)
bezeichnet man die Zentren „aktiver Galaxien“, die nicht nur im sichtbaren Bereich
des elektromagnetischen Spektrums große Energiemengen abstrahlen. Sie gehören zu
den entferntesten Objekten, die man kennt. Die Auswertung der Absorptionslinien in den
Spektren erlaubt den Rückschluss, dass sich elementare Naturkonstanten wie die Fein-
strukturkonstante, die Lichtgeschwindigkeit usw. auch im Laufe von Jahrmilliarden sowie
in den entlegensten Winkeln des Universums nicht geändert haben. Bilder: NASA/ESA
Hubble-Space Telecope / ESO Very Large Telescope (VLT).
Sind radiometrische Methoden überprüfbar?
Wie oben erwähnt, behaupten einige Kritiker, radiometrische Altersbestimmun-
gen sei angeblich nicht überprüfbar. Sie meinen, geochronologische Altersanga-
ben stünden im luftleeren Raum. Tatsächlich aber gibt es zahlreiche Methoden,
um die Größenordnungen geologischer Zeiträume unabhängig von radiometri-
schen Datierungen zu bestätigen.
Beginnen wir mit ein paar einfachen Beispielen: Die Kontinentaldrift liegt bei
wenigen Zentimetern pro Jahr. Damit sich Kontinente um Tausende von Kilome-
tern verschieben und ganze Gebirge auffalten können, braucht es sehr viel Zeit:
Hunderte von Jahrmillionen. Ein Mechanismus, der dies auch „kataklysmisch“ –
im Rahmen weniger Tausend Jahre – erklären könnte, ist nicht bekannt.
Ein besonders schönes Beispiel ist die Bremsung der Erdrotation durch den
Mond. Anhand mancher Sedimente lässt sich nachweisen, dass ein Jahr früher
deutlich mehr Tage hatte als heute bzw., dass die Tage kürzer waren. Als „Ta-
geszähler“ dienen Fossilien Kalk ausscheidender Organismen wie Korallen, Mu-
scheln und Stromatolithen. Interessant dabei ist, dass die Rate der Kalkfällung
bei Korallen täglichen und jährlichen Schwankungen unterliegt. Bei Muscheln er-
folgt die Kalkabscheidung nur während der Öffnung; sie variiert täglich und
halbmonatlich. Es ergibt sich demnach ein periodisches Muster; die Anzahl der
Tagesringe pro Jahr können in fossilen Korallen und Muscheln einfach ausgezählt
werden. Zählt man beispielsweise die Tagesringe von Fossilien aus dem Devon,
findet man, dass ein Jahr damals etwa 400 Tage hatte, ein Tag somit 22 Stunden
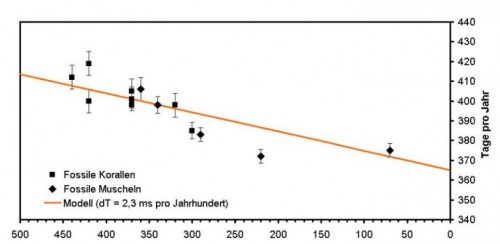
(Abb. 4). Zu Beginn des Kambriums zählt man im Mittel 428 Tagesringe pro Jahr
(LÖTHER 2004, 78), was einer Tageslänge von 20,5 Stunden entsprach.
Abb. 4: Anzahl der Tagesringe pro Jahr in fossilen Korallen und Muscheln.
Bild: © Thomas KLÜGEL (2006), geodätisches Informationszentrum Wettzel.
www.giz.wettzell.de/Vortraege/Erdrotation/Rotation_Erde.pdf
Wie ermittelt man daraus das Alter der Sedimente? Durch Auswertung zahlrei-
cher Beobachtungen aus den letzten 3000 Jahren sowie durch Bestimmung der
Zunahme der Mondentfernung (3,8 cm pro Jahr) mittels Laser und Reflektoren
lässt sich berechnen, wie stark die Verzögerung der Erdrotation durch Gezeiten-
reibung ungefähr ist: Im Durchschnitt werden die Tage pro Jahrhundert um rund
2 Millisekunden länger (STEPHENSON 2007, 44). Berechnet man anhand dieses
Werts, wieviel Zeit verstrichen ist, seit der Tag nur 20,5 bzw. 22 Stunden hatte,
erhält man bis auf 15 Prozent genau den allgemein akzeptierten Zeitpunkt des
Kambrium-Beginns von vor 545 Millionen Jahren sowie das Alter der Sedimente
des Devons von 350 bis 400 Millionen Jahren. Was zu belegen war.
Um die Zuverlässigkeit der Größenordnungen zu beurteilen, die geochronologi-
sche Datierungsmethoden durch Isotopenzerfall liefern, kann man sich auch ast-
ronomischer und kosmologischer Methoden bedienen. Das Alter von Sternen bei-
spielsweise ermittelt man üblicherweise über ihren thermonuklearen Zyklus, das
heißt über die nukleare Energieerzeugung. Die Berechnungen sind kompliziert,
man benötigt dafür Massen- und Druckgleichungen, Gleichungen über den Ener-
gietransport usw. Anhand physikalischer Modelle lässt sich allerdings klar ermit-
teln, wie lange es dauert, bis ein Stern (in Abhängigkeit von seiner Masse) seinen
Wasserstoffvorrat aufgebraucht hat.
Nach HERTZSPRUNG und RUSSELL besteht für die meisten Sterne eine mathema-
tisch präzise Beziehung zwischen ihrer absoluten Helligkeit, Masse und Oberflä-
chentemperatur (Spektraltyp): Je massereicher ein Stern ist, desto höher ist sei-
ne Oberflächentemperatur. Und je höher seine Temperatur ist, desto höher ist
sein Energieumsatz und desto heller leuchtet er. Trägt man in einem Diagramm
die absolute Helligkeit (in Magnituden) gegen die Oberflächentemperatur bzw.
den Spektraltyp auf, liegen die meisten Sterne entlang eines schmalen Ban-
des, der so genannten „Hauptreihe“. Dort verweilt der Stern die meiste Zeit und
fusioniert Wasserstoff in Helium. Anschließend verlässt er die Hauptreihe und
entwickelt sich zu einem so genannten Roten Riesen. Dieser Sterntyp entsteht,
wenn „Normalsterne“ einen bestimmten Teil ihres nuklearen Brennstoffs ver-
braucht haben und auf das so genannte Heliumbrennen umsteigen. Dieser Punkt
wird umso schneller erreicht, je größer die Anfangsmasse des Sterns war. Physi-
kalischen Berechnungen zufolge entwickeln sich Sterne mit der Masse unserer
Sonne nach etwa 11 Milliarden Jahren zu einem roten Riesen. Folglich sind
Sternhaufen, die masseärmere Sterne dieses Typs enthalten, entsprechend äl-
ter.
Durch systematische Untersuchungen von Sternhaufen fand man nun heraus,
dass eine Massenuntergrenze existiert, das heißt, man findet keine Roten Riesen,
die eine bestimmte Masse unterschreiten, weil sie dann älter sein müssten als
das Universum. Die Altersdaten, die man für die massenärmsten Roten Riesen
ermittelt hat, sind für den Kreationismus nicht weniger schwer verdaulich als ra-
diometrische Daten. Als Resultat findet man, dass die ältesten Sterne bzw.
Sternhaufen zwischen 10 und 14 Milliarden Jahre alt sind. Bis vor wenigen Jahren
lagen die Alter aus Kugelsternhaufen?Bestimmungen zwar deutlich über diesen
Werten, doch Verbesserungen in den Sternmodellen und den Methoden zur Al-
tersbestimmung haben diese Diskrepanz aufgehoben. Und die Daten decken
sich voll und ganz mit den Größenordnungen, die radiometrische Datie-
rungen liefern!
Der zweitälteste Stern ist HE 1523-0901 mit einem Alter von 13,2 Mrd. Jahren.
Sein Alter wurde über die Zerfallsreihe von Uran und Thorium in Kombination mit
Neutroneneinfang bestimmt. Es ist wiederum vergleichbar mit jenem Alter, das
man mit ganz anderen Methoden für das Universum bestimmt hat, beispielsweise
aus seiner Expansionsgeschichte oder der Analyse des kosmischen Mikrowellen-
hintergrundes. Durch Auswertung der Daten, welche die Raumsonden WMAP und
PLANCK geliefert haben, lässt sich das Alter des Kosmos sehr präzise auf 13,80 ±
0,04 Milliarden Jahren bestimmen. Diese Zahl passt zu dem Alter, welches man
für die ältesten Sterne ermittelt hat.
Fazit: Die Zuverlässigkeit radiometrischer Bestimmungsmethoden ist
nicht wissenschaftlich anfechtbar…
… denn sonst hätten sich längst derart viele Inkonsistenzen ergeben, dass der
Versuch, erdgeschichtliche und kosmische Ereignisse auch nur halbwegs einheit-
lich zu datieren, im Ansatz stecken geblieben wäre. Die verschiedenen kosmi-
schen und geochronologischen Datierungsmethoden führen unabhängig vonei-
nander mehr oder weniger zu denselben Altersangaben, die wir heute für die Er-
de, die ältesten Sterne und Sternhaufen sowie den Kosmos – teils bis in den
Promille-Bereich genau – ermittelt haben.
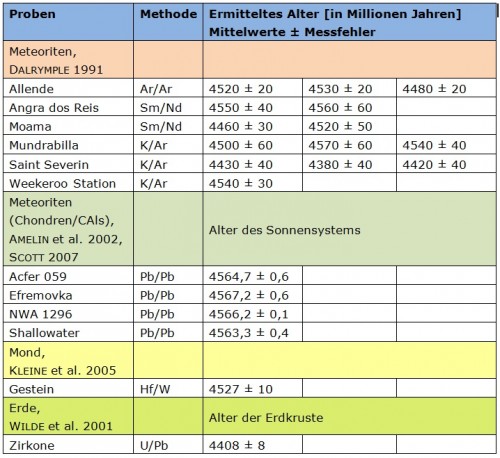
Die folgende Auflistung zeigt die Resultate einiger radiometrischer Altersbestim-
mungen von Meteoritenbestandteilen sowie von Gestein bzw. Mineralien von Erde
und Mond (Abb. 5). Die Ergebnisse repräsentieren die Entstehungsalter unseres
Sonnensystems sowie von Mond und Erde.
Abb. 5: Durchschnittliche Alterswerte verschiedener Meteoriten-Bestandteile sowie
Mineralien und Gesteinsproben von Erde und Mond. Die „Methode“ gibt an, welche
Nuklide für die Altersbestimmung herangezogen wurden (z. B. „K/Ar“ für den radio-
aktiven Zerfall von Kalium-40 zu Argon-40).
Wie man sieht, führen die verschiedensten radiometrischen Methoden (z.B. die
Kalium-Argon-Methode, Uran-Blei-Methode, die Samarium-Neodym-Methode
usw.) auch bei sehr unterschiedlichen Meteoriten- und Gesteinsproben immer
wieder zu dem allgemein akzeptierten Alter von Erde, Mond und Sonnensystem.
Man beachte insbesondere im Vergleich mit den Daten von DALRYMPLE (1991),
dass die Datierungen im Laufe der Zeit immer präziser wurden.
Würden all diese Rekonstruktionen keine realen Ereignisse bzw. Zeiträume wie-
derspiegeln, wäre die Übereinstimmung der ermittelten Altersangaben nicht zu
erklären. Denn warum sollten sich die Zerfallskonstanten der verschiedenen für
die Altersdatierung verwendeten Nuklide (Uran-235, Uran-238, Kalium-40, Neo-
dym-147 usw.) im Laufe der Zeit ausgerechnet immer so verändert haben, dass
man voneinander unabhängig immer die gleichen übereinstimmenden Altersda-
ten für bestimmte Gesteine oder Ereignisse erhält? Vernünftige Erklärungen da-
für hat man von Kritikern jedenfalls noch nicht gehört.
Und wie ist es zu erklären, dass Altersbestimmungen, die nicht auf radiometri-
schen Datierungen beruhen, wie die Auszählung von Tagesringen pro Jahr bei
fossilen Korallen und Muscheln, die Ermittlung der Geschwindigkeit der Kontinen-
taldrift, die Auswertung des kosmischen Mikrowellenhintergrundes, Warvenana-
lysen usw. in schöner Regelmäßigkeit die radiometrischen Ergebnisse bestätigen?
Dass sich die Fehler so „heraus mitteln“, dass ein einheitliches, in sich stimmiges
Bild der Erdgeschichte und kosmischen Entwicklung entsteht, ist extrem unwahr-
scheinlich, wenn man annimmt, dass es sich um illusionäre Zeiträume handelt.
Literatur
AMELIN, Y. et al. (2002) Lead isotopic ages of chondrules and calcium-aluminum-rich in-
clusions. Science 297, 1678–1683.
BARROW, J.D. (2011) Das Buch der Universen. Campus-Verlag, Frankfurt.
BOSCH, F. et al. (1996) Oberservation of bound-state-beta-decay of full ionized Re-187:
Re-187 – Os-187 cosmochronometry. Physical Review Letters 77, 5190-5193.
BOWLES, C. (2004) If the speed of light can change.
www.eurekalert.org/pub_releases/2004-06/ns-its063004.php
BRESTOWSKY, M. (2009) Evolution – ein Forschungsfeld im Grenzbereich. Naturwissen-
schaftliche Rundschau 62, 16-19.
DALRYMPLE, G.B. (1991) The age of the earth. Stanford University Press, Stanford.
GANDO, A.; DWYER, D. A.; MCKEOWN, R. D.; ZHANG, C. (2011) Partial radiogenic heat model
for Earth revealed by geoneutrino measurements. Nature Geoscience 4, 647–651.
KLEINE, T. et al. (2005) Hf-W chronometry of lunar metals and the age and early differen-
tiations of the moon. Science 310, 1671–1674.
KOTULLA, M. (2014) Gültigkeit und Grenzen geologischer Zeitbestimmung. www.wort-und-
wissen.de/loseblattsammlung/4-
01_Radiometrische_Methode_Uebersichtsblatt_v1403.pdf
LÖTHER, R. (2004) Zeit und Evolution der Lebewesen. Sitzungsberichte der Leibniz-
Sozietät 68, 67–78.
MCGRATH, A. (2001) Naturwissenschaft und Religion. Freiburg.
ROGNSTAD, M. (2005) Creationism and accelerated decay.
https://apps.usd.edu/esci/creation/age/content/creationism_and_young_earth/accel
erated_decay.html. Zugr. a. 26.05.2014.
SCOTT, E.R.D. (2007) Chondrites and the protoplanetary disk. Annual Review of Earth and
Planetary Sciences. 35, 577–620.
STEPHENSON, R.F. (2007) Warum die Tage länger werden. Spektrum der Wissenschaft 10,
44.
WILDE, S. A. et al. (2001) Evidence from detrital zircons for the existence of continental
crust and oceans on the earth 4.4 Ga ago. Nature 409, 175–178.
Die Zahlen geben an, wieviele Protonen und Neutronen („Nukleonen“) im Atomkern
enthalten sind. Die Zahl der Protonen ist charakteristisch für das jeweilige chemische
Element. So enthalten Uran-Kerne immer 92 Protonen. Folglich enthält Uran-238 zusätz-
lich 146 Neutronen, Uran-235 dagegen 143 Neutronen. Atomkerne mit gleicher Proto-
nenzahl (= Ordnungszahl) aber unterschiedlicher Neutronenzahl nennt man Isotope.
______________________________
Fußnote:
[1] Die Zahlen geben an, wieviele Protonen und Neutronen („Nukleonen“) im Atomkern enthalten
sind. Die Zahl der Protonen ist charakteristisch für das jeweilige chemische Element. So
enthalten Uran-Kerne immer 92 Protonen. Folglich enthält Uran-238 zusätzlich 146 Neutronen,
Uran-235 dagegen 143 Neutronen. Atomkerne mit gleicher Protonenzahl (= Ordnungszahl) aber
unterschiedlicher Neutronenzahl nennt man Isotope.


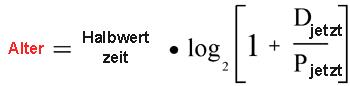











Kommentare (342)