Und dieses Ergebnis setzen wir nun als neuen Startwert ein:
Und so weiter:
Ich spare mir jetzt das ausführliche Aufschreiben der Formel und zeige euch nur noch die Ergebnisse:
Und jetzt spare ich mir auch noch das weiterrechnen, denn ich mache es derzeit so wie May damals und tippe das selbst alles händisch in den Taschenrechner. Aber man sieht deutlich, dass sich die Werte immer mehr annähern und vermutlich irgendwann in der Nähe von x=0,6 landen werden. Irgendwann werden wir einen Attraktor erreicht haben; einen Fixpunkt also, bei dem dann der neue Wert von x gleich dem alten ist, wenn man die Formel ausrechnet. Und das gilt für jeden Startwert: Hätte ich in dem Rechenbeispiel vorhin nicht mit x=0,5 sondern mit x=0,1 oder irgendeiner anderen Zahl begonnen, wäre ich am Ende trotzdem wieder in der Nähe von 0,6 gelandet.
Dieses Ergebnis war in etwa auch das, was man sich erwartet hat. Die Größe einer Population sollte sich irgendwann stabilisieren und an die äußeren Bedingungen angepasst haben. Aber ein genauerer Blick auf die Formel zeigte Komplikationen. Setzt man als Wert für den Wachstumsparameter r eine Zahl ein, die größer als 3 ist, dann gab es keinen Fixpunkt mehr. Würde man das gleiche Spiel wie vorhin mit r=3,1 spielen und alles durchrechnen, dann gäbe es keine einzige Zahl, an die sich x immer weiter annähert. Man würde beobachten, wie der Wert für x irgendwann immer zwischen zwei Zahlen hin und her springt! In der biologischen Interpretation würde das bedeuten, dass sich die Größe der Population nicht irgendwann bei einer bestimmten Zahl von Individuen einpendelt, sondern von Jahr zu Jahr zwischen zwei bestimmten Werten hin und her wechselt. Im einen Jahr wäre x ungefähr gleich 0,5; im nächsten Jahr dann ungefähr gleich 0,7. Dann folgt wieder ein Jahr mit x~0,5 und im nächsten sind es wieder 0,7. Und so weiter.
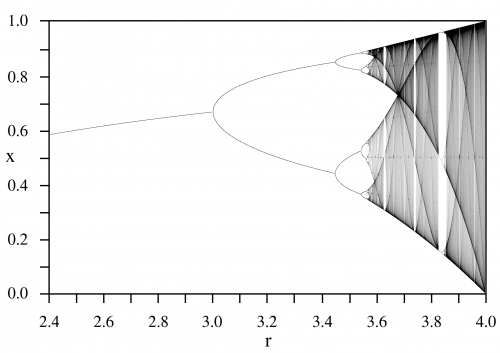
Das war schon seltsam genug. Aber als May noch mehr Werte für r ausprobiert hat, fand er, dass x irgendwann nicht mehr zwischen zwei Zahlen wechselt, sondern vier. Und dann zwischen acht. Und irgendwann gab es überhaupt kein Muster mehr und die Zahlen wechselten völlig unvorhersagbar zwischen 0 und 1 hin und her. Das ganze war enorm verwirrend – aber zumindest konnte man damit ein schönes Bild zeichnen, das in der Chaosforschung fast so berühmt ist, wie der Lorenz-Attraktor aus dem letzten Artikel. So sieht es aus:
Das ist das sogenannte “Bifurkationsdiagramm der logistischen Gleichung”. Auf der x-Achse ist der Wert für den Wachstumsparameter r aufgetragen und auf der y-Achse die Werte für x, bei denen man mit der logistischen Gleichung am Ende landet. Zuerst bekommt man für jeden Wert von r immer nur einen Fixpunkt. Dann sind es auf einmal zwei, die sich nochmal aufspalten und vier werden, dann acht, und so weiter. Die Perioden verdoppeln sich immer schneller, bis irgendwann das völlige Chaos ausbricht!
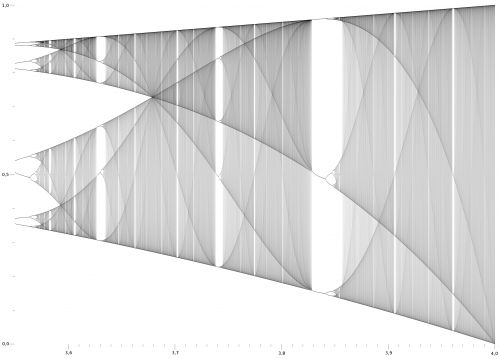
Aber wer genau schaut, wird etwas überraschendes entdecken: In der Nähe von r=3,8 scheint wieder etwas Ordnung einzukehren. Das Chaos zieht sich zurück und plötzlich kriegt man dort wieder nur eine periodische Lösung von wenigen Zahlen, zwischen denen die logistische Gleichung hin und her springt. Und tatsächlich sieht eine Vergrößerung dieses Bereichs so aus:
Die Vergrößerung des Ausschnitts sieht (fast) so aus wie das Original. Im Ausschnitt erkennen wir die gleiche Abfolge von Fixpunkten, Periodenverdoppelung und Chaos. Und im Chaos ein weiteres Fenster mit periodischen Fixpunkten… Ihr könnt euch gerne selbst ein Computerprogramm schreiben, das diese Bilder zeichnet (oder dieses Online-Programm nutzen) und werdet feststellen, dass man tatsächlich immer weiter Ausschnitt für Ausschnitt vergrößern kann und dabei immer wieder auf das gleiche Bild stoßen wird.











Kommentare (13)