Resonanzen wie die eben beschriebene nennt man “Resonanzen der mittleren Bewegung” (oder “mean-motion resonances”). “Bewegung” wird aber in diesem Zusammenhang etwas umfassender definiert. Es geht nicht nur um die Bewegung eines Himmelskörpers durch den Raum, sondern auch um die Veränderung seiner Bahn. Die Bahnen der Himmelskörper sind ja variabel; sie werden größer oder kleiner; mehr oder weniger elliptisch und drehen sich im Raum hin und her. Es kann nun auch passieren, dass die Geschwindigkeit, mit der sich zum Beispiel die Bahn eines Asteroiden dreht in einem ganzzahligen Verhältnis zur Drehgeschwindigkeit der Bahn eines Planeten stehen. Oder die Periode mit der eine Bahn hin und her wackelt steht in einem ganzzahligen Verhältnis zur Wackelei einer anderen Bahn. All diese Resonanzen nennt man “säkulare Resonanzen” und sie spielen eine wichtige Rolle, wenn es um die Dynamik von Satelliten geht.
Das Problem ist nun, dass es bei der Bewegung von künstlichen Himmelskörpern sehr viele solcher säkularer Resonanzen gibt. Welche davon wie stark wirksam werden, hängt von vielen Faktoren ab. Davon, wie nah oder weit man von der Erde entfernt ist zum Beispiel oder welche Zeitskalen man betrachtet. Manche säkularen Resonanzen hängen mit der Rotation der Erde zusammen und laufen daher mit Perioden von wenigen Tag ab; andere werden durch die Bewegung der Erde um die Sonne verursacht und dauern Jahre. Wieder andere hängen damit zusammen, wie sich die Bahn des Mondes verändert oder wie die Erdachse im Laufe der Zeit hin und her schwankt und wirken sich daher erst im Laufe von Jahrzehntausenden aus. Rosengren und seine Kollegen haben sich bei ihrer Analyse auf die Navigationssatelliten konzentriert. Die befinden sich einige zehntausend Kilometer von der Erde entfernt und haben unterschiedlich stark geneigte Umlaufbahnen, um die gesamte Erde im Blickfeld haben zu können. Diese verschiedenen Bahnneigungen machen sie zu einem guten Studienobjekt – und ihre technische Bedeutung zu einem wichtigen Anwendungsfall!
In ihrer Arbeit haben die Wissenschaftler außerdem nur die Störungen betrachtet, die vom Mond verursacht werden (bei den solaren Resonanzen sind die Zeitskalen so lang, dass man sie vorerst vernachlässigen kann). Ihre Arbeit war analytisch, das heißt sie haben nicht wie sonst meistens üblich, die Bewegung der Satelliten numerisch am Computer simuliert um herauszufinden, ob sie sich irgendwann chaotisch bewegen. Arbeiten dieser Art wurden in der Vergangenheit schon gemacht und sie haben gezeigt, dass es tatsächlich unter vielen unterschiedlichen Bedingungen zu instabilen Satellitenbahnen kommen kann. Rosengren und seine Kollegen wollten aber nicht nur wissen ob Chaos auftritt, sondern auch warum und dafür müssen sie die entsprechenden mathematischen Gleichungen genau betrachten und mathematisch lösen, anstatt sie am Computer nur näherungsweise zu simulieren. Dieses Arbeitsgebiet der Mathematik nennt sich “Störungsrechnung”, ist ziemlich knifflig und wer mehr darüber wissen will, soll sich am besten meine Artikelserie zu diesem Thema ansehen (Teil 1, Teil 2, Teil 3, Teil 4). Im Wesentlichen geht es darum, eine sogenannte “Störungsfunktion” aufzustellen, die alle möglichen säkularen Resonanzen mathematisch zusammenfasst und diese Funktion zu untersuchen. Wer gerne mal wissen möchte, wie so etwas aussieht – bitte sehr:
Ich werde das jetzt nicht im Detail erklären (das könnte ich auch gar nicht, ohne mich nochmal ein paar Wochen hinzusetzen und all das aufzufrischen, was ich damals im Studium gelernt habe). Am Ende geht es um zwei ganz bestimmte Größen: die “Länge des aufsteigenden Knotens” und das “Argument des Perihels”. Das sind zwei der sogenannten “Bahnelemente”, mit denen man die Bahn eines Himmelskörpers beschreiben kann. Knotenlänge und Argument des Perihels sind zwei der drei Winkel, die angeben, wie die Bahn im Raum orientiert ist und so wie alle anderen Bahnelemente verändern sie sich im Laufe der Zeit. Stehen nun die Änderungsraten von Knotenlänge/Argument des Perihels der Mond- bzw. Satellitenbahn in bestimmten ganzzahligen Verhältnissen, dann kommt es zu einer säkularen Resonanz und genau das war es, was Rosengren und seine Kollegen untersucht haben. Hier ist ein Beispiel für ihre Ergebnisse:

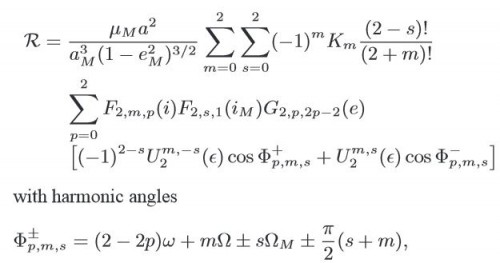










Kommentare (7)