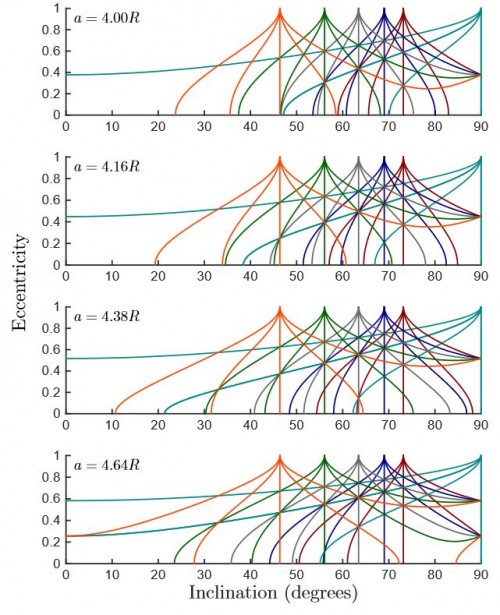
Die vier Diagramme zeigen die Parameter für vier verschiedene Navigationssatellitensysteme: GLONASS (Russland), GPS (USA), BeiDou (China) und Galileo (Europa). In jedem Bild zeigen die Achsen die Werte für die Bahnneigung und die Bahnexzentrizität an. Die bunten Linien sind die Positionen unterschiedlicher säkularer Resonanzen. Soll heißen: Ein Satellit, dessen Bahnneigung und Bahnexzentrizität Werte haben, die in dem Diagramm genau auf einer der bunten Linien liegen, wird von einer Resonanz beeinflusst. Auch ohne alle Details der Bilder zu verstehen, sieht man eines doch sehr deutlich: Es gibt viele Resonanzen, sie liegen einander oft sehr nahe und sie überlappen sich gegenseitig. Und damit ist man mitten im Chaos. Denn wenn sich ein Satellit in einer der Überlappungsregionen befindet, reichen oft schon kleine Veränderungen in der Bahn aus, um von einer Resonanz in die andere zu “springen” und damit die ganze Bahndynamik zu verändern (das ist genau das Verhalten, das ich auch schon bei der Betrachtung der seltsamen Attraktoren beschrieben habe.
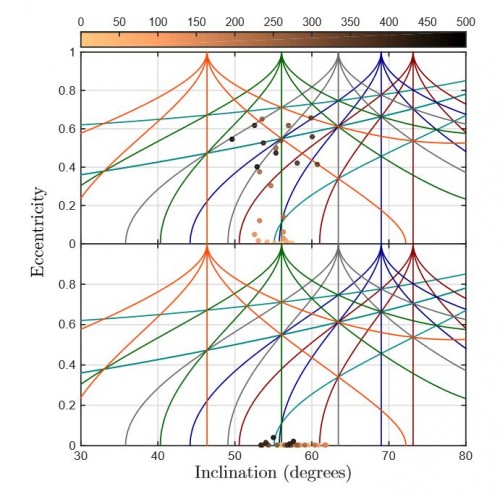
Rosengren und seine Kollegen haben das auch mit konkreten Beispielen illustriert. Das zeigt dieses Bild:
Hier sieht man die dynamische Entwicklung zweier fiktiver Galileo-Satillten im Verlauf von 500 Jahren. Die Bahnen der Satelliten sind anfangs identisch, nur ist eine Bahn um 120 Grad gegenüber der anderen gedreht (um die sogenannten Knotenlinie herum, also die Linie, die die beiden Schnittpunkte der Satellitenbahn mit der Ebene der Erdbahn verbindet). Die Diagramme sind identisch mit denen zuvor; nur sind diesmal Punkte eingetragen, die zeigen, wie sich Bahnneigung und Exzentrizität der Satelliten im Laufe der Zeit verändern. Die Farbe der Punkte gibt dabei den Zeitpunkt an (je heller, desto früher). Beim unteren Bild passiert nicht viel – die Bahn des Satelliten bleibt immer annähernd kreisförmig, das heißt seine Exzentrizität ist gleich Null und die Punkte landen alle auf der x-Achse. Beim oberen Bild sieht man aber gut, wie die Exzentrizität im Laufe der Zeit immer mehr anwächst und sich am Ende der 500 Jahre immer stärker ändert. Wenn die Bahn eines Satelliten aber zu sehr von der Kreisbahn abweicht, kommt er an seinem erdnächsten Punkt der Erde immer näher und damit auch der Atmosphäre, was schließlich durch die Reibung zu einem Absturz bzw. seiner Zerstörung sorgt.
Die Arbeit von Rosengren und seinen Kollegen zeigt also recht deutlich die Komplexität der chaotischen Dynamik auf. Nicht nur kommt es darauf an, ob man sich in einer Region befindet, in der Resonanzen wirksam sind bzw. sich überlappen oder nicht, sondern auch die ursprüngliche Konfiguration der Bahn spielt eine wichtige Rolle. Wie das eben so ist, wenn das Chaos eine Rolle spielt: Dann können schon kleinste Änderungen in den Anfangsbedingungen dramatische Auswirkungen haben. Die Drehung der Mondbahn im Laufe der Zeit – sie braucht knapp 19 Jahre für eine Drehung um die Knotenlinie – hat einen relevanten Einfluss auf die Stabilität von Satellitenbahnen und die Komplexität der säkularen Resonanzen ist der Grund, warum man bis jetzt Schwierigkeiten, eine stabile “Friedhofsregion” für die Galileo-Satelliten ausfindig zu machen. Rosengren und seine Kollegen wollen aber in zukünftigen Arbeiten genau dieses Chaos ausnutzen und zeigen, wie es für eine aktive Entfernung des Weltraumschrotts genutzt werden kann. Anstatt die ausgedienten Satelliten “sicher” zu parken, was angesichts der Resonanzen schwierig wird, sollen sie durch das Chaos gezielt abstürzen. Aber damit das klappt, muss man sich noch ein wenig intensiver mit der Identifizierung der Resonanzen beschäftigt. Davon gibt es erdnahen Weltraum noch jede Menge…











Kommentare (7)