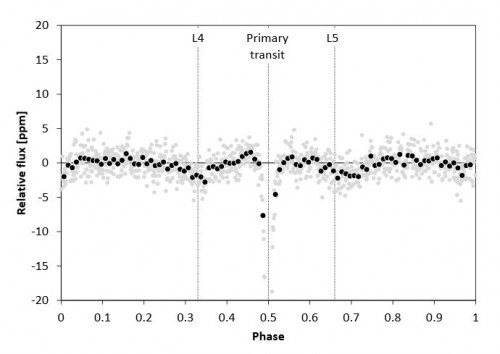
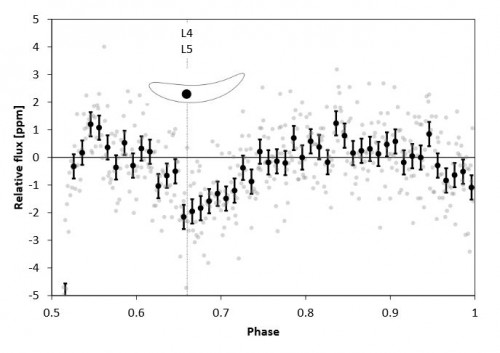
Das erste Bild zeigt, dass hier nun tatsächlich etwas zu erkennen ist. Das zweite Bild zeigt die Sache noch einmal genauer. Die Form der Lichtkurve sollte im Fall des Transits eines Trojanerplaneten ein ganz bestimmtes Aussehen haben. Denn so ein Planet sitzt nicht exakt im Lagrangepunkt und bleibt immer exakt 60 Grad vor bzw. hinter dem Hauptplaneten, sondern befindet sich im Allgemeinen mal ein wenig vor dem Lagrangepunkt, mal ein wenig dahinter. Aus der Sicht des Lagrangepunktes bewegt sich ein Trojaner in einer “Kaulquappen”-förmigen Bahn um ihn herum, so wie im zweiten Bild skizziert (Ich habe in diesem Artikel erklärt, wie das genau funktioniert).
Und die Form der Lichtkurve entspricht in etwa dem, was man erwarten würde, wenn der zusätzliche Transit von Trojanerplaneten hervorgerufen wurde!

Künstlerische Darstellung vom PLATO-Weltraumteleskop (oben rechts) und jeder Menge Planeten (Ein besseres Bild scheint es von dem Ding nicht zu geben… Bild: DLR, CC-BY 3.0)
Die Ergebnisse dieser Untersuchung sind leider noch nicht statistisch signifikant genug, um tatsächlich auf die Existenz von extrasolarern Trojaner schließen zu können. Aber sie zeigen, dass es sich auf jeden Fall lohnt, weiter zu suchen! Hippke und Angerhausen verweisen auf das PLATO-Weltraumteleskop (ein Projekt des Deutschen Zentrums für Luft- und Raumfahrt), das im Jahr 2024 ins All fliegen soll und dann wesentlich mehr und bessere Daten sammeln kann. Mit denen würde sich die Frage nach den extrasolaren Trojaner vielleicht beantworten lassen. Aber wer weiß: In der Zwischenzeit findet man ja vielleicht auch auf anderem Weg die Trojaner fremder Sterne! (Und ich kann der DFG dann endlich einen Brief schreiben und ihnen sagen: “Ha! Ich habs euch gesagt!”)











Kommentare (39)