Hurra! Heute ist der Internationale Pi-Tag. Einmal im Jahr ignorieren wir die Vernunft und erfreuen uns daran, dass in der seltsamen amerikanischen Schreibweise das heutige Datum “3/14” lautet und somit die ersten Stellen der wunderbaren Kreiszahl Pi andeutet.
Als offizieller Botschafter der Zahl Pi des Vereins der “Freunde der Zahl Pi” muss (und will!) ich diesen Tag natürlich nutzen, um der Welt wieder ein wenig die frohe Kunde der Kreiszahl zu bringen. Das habe ich früher schon oft gemacht (hier oder hier oder hier oder hier). Ich habe über Pi und galaktische Balken geschrieben und über die faszinierende Frage nach der Normalität von Pi.

Backt euch doch heute mal ne Pi-Torte! Ihr müsst auch nicht “Florian” drauf schreiben (könnt ihr aber gerne!)
Ganz besonders gerne erzähle ich am Pi-Tag auch immer von Albert Einstein. Der hat nicht nur heute Geburtstag, sondern auch eine (relativ unbekannte) Arbeit über die Mäanderbildung von Flüssen geschrieben, die ein weiteres Mal zeigt, das Pi überall ist. Aber am 14. März wurde nicht nur Albert Einstein geboren. Der heutige Tag ist auch der Todestag von Robert Hooke. Vor genau 315 (Verdammt! Ich hätte diesen Artikel letztes Jahr schreiben sollen!) Jahren ist der britische Universalgelehrte gestorben. Robert Hooke kennt man heute vor allem für seine ausgiebige Streiterei mit Isaac Newton (ich habe in aktuellen Buch* darüber berichtet). Oder vielleicht auch noch von seiner grundlegenden Arbeit zur Mikroskopie. Sein Buch “Micrographia” war einer der ersten großen Bestseller der (populär)wissenschaftlichen Literatur. Aber Hooke hatte auch noch jede Menge andere Interessen. Natürlich auch die Astronomie und auf diesem Gebiet hat er sich mit einer Frage beschäftigt, die fundamentaler kaum sein könnte: Wie weit entfernt sind die Sterne!

Von Hooke ist kein Porträt überliefert. Aber Denkmäler und Inschriften gibt es! (Bild: Rita Greer, CC-BY-SA 3.0)
Man darf nicht vergessen, in welcher Zeit Hooke gelebt hat. Im 17. Jahrhundert war es noch gar nicht so lange her, dass sich die Gelehrten zu einem heliozentrischen Weltbild durchgerungen hatten. Die Arbeiten von Kopernikus, Galilei und Kepler waren überzeugend, aber eine Sache war bei der Angelegenheit immer noch komisch. Wenn sich tatsächlich die Erde um die Sonne bewegt und wir mit der Erde gemeinsam ständig durchs Weltall sausen, dann muss sich ja auch unser Blickwinkel auf die Sterne ständig verändern. Und dann müssten wir eine scheinbare Verschiebung ihrer Position beobachten. Das ist genau der gleiche Effekt, den man auch sieht, wenn man mit dem Auto durch die Gegend fährt. Der Blickwinkel auf die Landschaft verändert sich ständig und wenn man dann zum Beispiel ferne Häuser betrachtet und deren Position mit der von noch ferneren Bergen vergleicht, dann bewegen sich die Häuser im Vordergrund vor den Bergen im Hintergrund.
Das sollten auch die Sterne machen: Die uns näheren Vordergrundsterne sollten sich vor den Hintergrundsternen bewegen. Sie sollten im gleichen Rhythmus hin und her wackeln, in dem sich auch die Erde um die Sonne bewegt. Aber wie sehr man die Sterne auch beobachtet hat: Sie blieben alle dort, wo sie waren. Das war lange Zeit auch eines der stärksten Argumente gegen ein heliozentrisches Weltbild. Jeder konnte sehen dass sich die Sterne – und damit die Erde – nicht bewegen!
Wie gesagt: Man darf nicht vergessen, in welcher Welt die Menschen damals gelebt haben. Heute ist es für uns selbstverständlich, das Universum als unvorstellbar groß und die Sterne als unvorstellbar weit entfernt zu betrachten. Damals war es aber noch gar nicht so lange her, dass das “Universum” nur aus der Erde, Sonne, Mond und den Planeten bestand und außen herum war ne Sphäre an der Fixsterne klebten. Und auch als sich das heliozentrische Weltbild durchgesetzt hatte, wusste man nichts von Galaxien und den wahren Ausmaßen des Kosmos. Man wusste halt nur, dass die Sterne weiter entfernt sein mussten als bisher gedacht. Denn je weiter sie weg sind, desto kleiner fällt auch die scheinbare Positionsveränderung aus. Da aber niemand wusste, WIE weit sie jetzt wirklich entfernt sind, konnte auch niemand sagen, wie klein der Effekt ist und wie groß die Chancen sind, ihn zu beobachten.
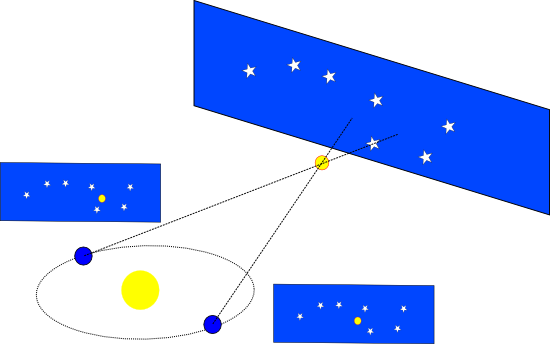
Wenn die Erde sich bewegt müssen die Sterne das auch tun (Bild: WikiStefan, CC-BY-SA 3.0)
Aber wenn Wissenschaftler eines nicht leiden können, dann sind das offene Fragen! Also haben sie sich bemüht, eine Antwort zu finden und mit dabei war Robert Hooke. Zwischen 1669 und 1670 hat er den Stern Gamma Draconis betrachtet. Er hat ihn ausgewählt, weil er von London aus gesehen direkt im Zenit steht, also direkt über dem Beobachter am Himmel. So ein Stern sollte die größte scheinbare Positionsverschiebung zeigen, wenn sich die Erde einmal um die Sonne herum bewegt. Seine Beobachtungen hat er dann unter dem Titel “An attempt to prove the motion of the earth from observations” veröffentlicht. Darin verkündet er, er habe eine “Parallaxe” von 30 Bogensekunden gemessen.
“Parallaxe” ist das Wort, mit dem die Astronomen den Winkel beschreiben, der der scheinbaren Positionsänderung entspricht. Jeder Stern muss aufgrund der Bewegung der Erde im Laufe eines Jahres eine kleine Ellipse am Himmel beschreiben. Die Winkelausdehnung dieser Ellipse ist umso größer, je näher der Stern ist. Eine Parallaxe, d.h. ein Winkel von 30 Bogensekunden würde einer Entfernung von etwa 40 Lichttagen entsprechen. Tatsächlich ist Gamma Draconis aber 154 Lichtjahre entfernt und die korrekte Parallaxe beträgt nur 21 Milli-Bogensekunden. Hookes Messungen waren also deutlich zu groß; oder anders gesagt: Was auch immer er da zu messen geglaubt hatte, hatte nichts mit der tatsächlichen scheinbaren Bewegung des Sterns zu tun.
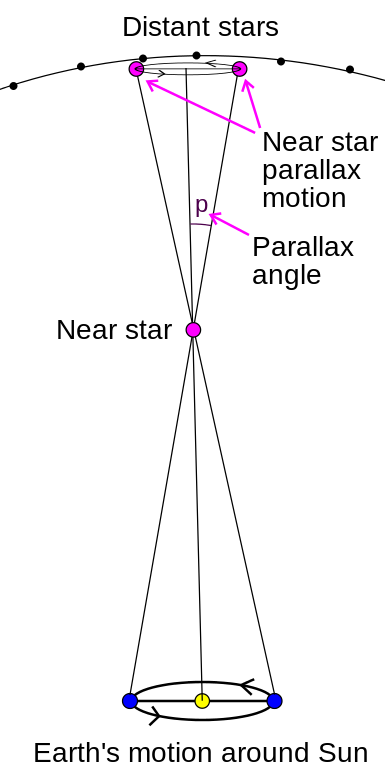
Da steht p! Da sollte π stehen! (Bild: Booyabazooka, public domain)
Dass Robert Hooke nicht der erste war, der die Entfernung der Sterne gemessen hatte, hat sich aber erst später herausgestellt. Tatsächlich hat es bis zum Jahr 1838 gedauert, bevor Friedrich Wilhelm Bessel die erste korrekte Entfernungsmessung bei einem Stern gelungen ist. Wer mehr zu dieser ganzen Geschichte wissen will, dem empfehle ich dringend das Buch “Parallax: The Race to Measure the Cosmos”* von Alan Hirshfeld.
Zum Abschluss gehen wir wieder zurück zum Anfang. Zur Kreiszahl Pi. Die findet man hier natürlich auch. Zum Beispiel im Symbol, mit dem die Parallaxe oft bezeichnet wird: π:
Wobei a der Durchmesser der Erdbahn ist und r der Abstand des Sterns von der Sonne. Robert Hooke war also auf der Suche nach dem Wert von π. Nur eben in dem Fall nicht nach dem Wert der fundamentalen Kreiszahl sondern nach der ebenso fundamentalen Distanz der Sterne. Dass er dabei gescheitert ist, macht den Versuch nicht weniger lobenswert. Und sein Todestag am 14.3. passt da irgendwie ganz gut dazu…
Ich wünsche allen einen schönen Pi-Tag!
P.S. Wer Mitglied im Verein der Freunde der Zahl Pi werden möchte kann sich gerne an mich wenden. Als Pi-Botschafter kann ich die entsprechende Aufnahmsprüfung (bei der man 100 Nachkommastellen auswendig aufsagen muss) abnehmen.
P.P.S. Ja, ich kenne die Sache mit Tau. Und halte sie für Unfug – siehe hier











Kommentare (28)