Die Milchstraße ist die Galaxie, in der sich unsere Sonne befindet. Also quasi “unsere” Gegend im Universum. Man sollte annehmen, das wir gerade diese Ecke besonders gut kennen. Und das ist natürlich auch so. So gut wie alles, was die Astronomie in den letzten Jahrhunderten über Sterne und Planeten herausgefunden hat, hat sie über Sterne und Planeten herausgefunden, die Teil der Milchstraße sind. Wenn es aber um die Milchstraße als Ganzes geht, dann wird es kompliziert. Zum Beispiel was die Frage nach ihrer Form angeht. Andere Galaxien sind so weit entfernt, das wir sie in ihrer Gesamtheit im Teleskop sehen und daher auch leicht ihre Form bestimmen können. Bei der Milchstraße liegt aber unser Beobachtungspunkt mitten drin. Wir sehen quasi den Wald vor lauter Bäumen nicht und deswegen ist es schwer, ein genaues Bild der Form und Struktur unserer eigenen Galaxis zu gewinnen.
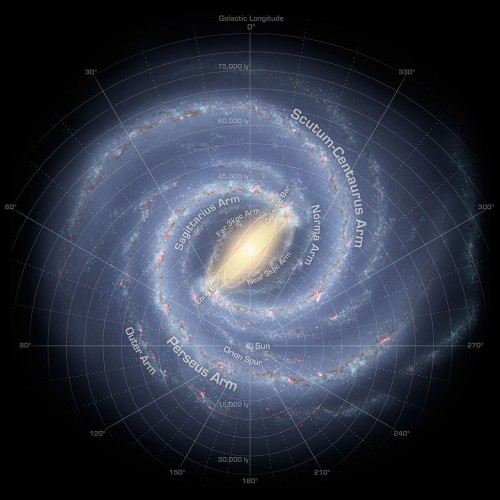
So sieht die Milchstraße vielleicht aus. Oder auch nicht. Ganz genau wissen wir es noch nicht. (Künstlerische Darstellung: NASA/JPL-Caltech/R. Hurt)
Auch die Frage nach der Gesamtmasse der Milchstraße ist nicht leicht zu beantworten. Wie “wiegt” man eine ganze Galaxie? Man könnte einfach alle Sterne zählen und ihre Massen addieren. Aber abgesehen davon, dass es nicht einfach ist herauszufinden, wie viele Sterne da überhaupt sind, hilft uns das nicht weiter. Denn es gibt ja neben den leuchtenden Sternen auch die nicht leuchtende dunkle Materie.
Man kann nun aber die Bewegung der sichtbaren Sterne beobachten. Die wird durch die gesamte Masse der Milchstraße bestimmt; egal ob sie dunkel ist oder hell. Das hat man in der Vergangenheit getan (und so überhaupt erst gemerkt, dass es eine dunkle Materie geben muss). Damit kam man auf eine Masse, die irgendwo zwischen 700 Milliarden und 2000 Milliarden Sonnenmassen liegen muss.
Das Problem bei dieser Methode ist Johannes Kepler. Beziehungsweise kann der gute Kepler natürlich nichts dafür, dass die Massebestimmung ungenau ist. Aber er hat uns gezeigt, dass die Planeten sich nicht immer mit der gleichen Geschwindigkeit um die Sonne bewegen. Das besagt das zweite seiner berühmten drei Gesetze zur Planetenbewegung: Ein Planet ist um so schneller, je näher er der auf seiner Bahn der Sonne kommt. Und das erste Gesetz besagt, dass die Planeten sich nicht auf kreisförmigen Bahnen bewegen und deswegen während eines Umlaufs tatsächlich mal näher und mal weiter entfernt von der Sonne sind.
Die Bewegung der Sterne um das Zentrum der Milchstraße ist nicht direkt mit der der Planeten um die Sonne vergleichbar; sie ist nicht so geordnet und viel chaotischer. Aber auch hier bewegen sich die Sterne unterschiedlich schnell, je nach Abstand vom Zentrum und auch hier verändert sich der Abstand zum Zentrum ständig. Da es dann auch noch mehrere Millionen Jahre dauert, bis ein Stern eine Runde um das Zentrum der Milchstraße absolviert hat (bei der Sonne mehr als 200 Millionen Jahre), ist es nicht leicht, diesen Effekt genau zu bestimmen. Man müsste enorm lange (oder enorm genau) beobachten, um zu wissen, auf welchen Abschnitt seiner Umlaufbahn ein Stern sich gerade befindet und welcher Anteil seiner Geschwindigkeit der Gesamtmasse der Milchstraße und welcher Anteil Johanns Kepler zu verdanken ist.
Nun aber haben Ekta Patel von der Universität Arizona und ihre Kollegen eine neue Methode ausprobiert (“Estimating the Mass of the Milky Way Using the Ensemble of Classical Satellite Galaxies”). Sie haben die Rotation der vielen kleinen Satellitengalaxien betrachtet, die gravitativ an unsere Milchstraße gebunden sind. Auch die wird von der Gesamtmasse der Milchstraße bestimmt. Ihr Drehimpuls verändert sich allerdings nicht so einfach wie die Geschwindigkeit der Sterne. Ohne äußere Einflüsse bleibt er konstant.
Patel und ihre Kollegen haben nun sehr ausführliche Computersimulationen durchgeführt (es wurden circa 20.000 Galaxien plus Satellitengalaxien simuliert) um zu schauen, welche Masse der Hauptgalaxie am besten zur Rotationsgeschwindigkeit unserer Satellitentgalaxien passt. Das Ergebnis: Irgendwo zwischen 670 und 1240 Milliarden Sonnenmassen muss die Masse unserer Milchstraße liegen. Vermutlich bei 960 Milliarden Sonnenmassen. Das passt nicht nur sehr gut zu den bisherigen Massenbestimmungen, sondern ist auch viel genauer.
Wir kennen jetzt also nicht nur die Masse unserer eigenen Milchstraße besser als zuvor. Diese neue Methode wird uns auch dabei helfen, die Massen anderer Galaxien genauer zu bestimmen. Und das ist doch nett!












Kommentare (8)