Die Europäische Südsternwarte (ESO) hat Materie beobachtet, die in das gigantische schwarze Loch im Zentrum unserer Milchstraße fällt. Die Beobachtung war so detailliert wie nie zuvor und das, was man beobachtet hatte, konnte in dieser Form noch nie beobachtet werden. Diese wissenschaftliche Forschung ist es absolut wert, darüber berichtet zu werden. Und das haben auch sehr viele Medien getan. Und überall wurde auch ein Bild veröffentlicht, das den Fall der Materie in das schwarze Loch zeigt. Stellvertretend sei hier der Artikel auf futurezone.at (WebCite) genannt, der aufgeregt mit “Schwarzes Loch? Südsternwarte zeigt unfassbare Aufnahme” anfängt und mit “Die Europäische Südsternwarte zeigt das detaillierteste Bild von Materie, die um das Schwarze Loch kreist” weitergemacht. Und dazwischen ist dieses Bild zu sehen:

Eine COMPUTERSIMULATION (!!!) der Bewegung von Material in der Nähe eines schwarzen Lochs (Bild: ESO/Gravity Consortium/L. Calçada)
Und wenn ich einen Artikel schon mal so anfange, dann wird den meisten natürlich klar sein, wie es weiter geht. Nein, dieses Bild ist KEINE Aufnahme der Europäischen Südsternwarte. Man “sieht” dort nicht, wie Material in ein schwarzes Loch fällt. Es ist eine Computersimulation, die das Verhalten von Materie in der Nähe eines schwarzen Loches simuliert. Was die ESO auch in ihrer Pressemitteilung genau so sagt. Aber sie sieht zugegebenermaßen viel beeindruckender aus, als die echte Daten der Wissenschaftler:
Ich werde jetzt gar nicht im Detail erklären, was da zu sehen ist; das ist auch nicht so wichtig. Ich erkläre lieber, was die Astronominnen und Astronomen tatsächlich erforscht haben.
Dass im Zentrum jeder Galaxie und damit auch unserer eigenen Milchstraße ein supermassereiches schwarzes Loch mit der millionen- bis milliardenfachen Masse unserer Sonne sitzt, wissen wir schon lange. Und weil schwarze Löcher so interessante Objekte sind, erforschen wir sie natürlich auch. Das ist knifflig, weil schwarze Löcher per Definition nicht zu sehen sind. Aber ihre Umgebung sehr wohl und aus ihrer Beobachtung können wir ableiten, was das schwarze Loch so treibt.
Beim schwarzen Loch im Zentrum unserer Galaxie – das auf den schönen Namen SgrA* hört – ist das vor allem der Stern S2 (über den ich hier mehr erzählt habe). Er umkreist das schwarze Loch und aus seiner Bewegung konnten wir nicht nur bestätigen, dass das schwarze Loch tatsächlich ein schwarzes Loch und nicht irgendwas anderes ist. Sondern auch ein paar interessante Eigenschaften ableiten.
Aber in der Nähe so eines supermassereichen schwarzen Lochs gibt es normalerweise noch mehr Zeug Große Mengen an Gas und Staub zum Beispiel. Das ganze Material wird durch die Gravitationskraft des Lochs beeinflusst: Es bewegt sich rund um das Loch herum und bildet eine große Scheibe, aus der immer wieder mal etwas IN das Loch fällt.
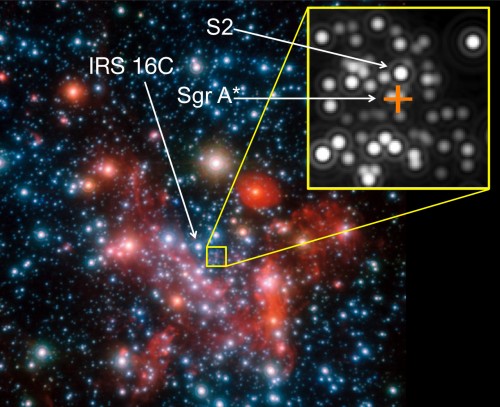
Stern S2 im Zentrum der Milchstraße (Bild: ESO/M. Kornmesser)
Genau das wollten die Astronomen der GRAVITY Collaboration beobachten und ihre Ergebnisse haben sie kürzlich veröffentlicht (“Detection of orbital motions near the last stable circular orbit of the massive black hole SgrA*”). GRAVITY ist das virtuelle Teleskop, das sie für ihre Arbeit benutzt haben. Und “virtuell” ist es deswegen, weil es eigentlich nicht existiert. Also natürlich schon, die Wissenschaftler haben es sich nicht einfach nur ausgedacht! Aber GRAVITY ist ein sogenanntes “Interferometer”. Was das ist habe ich früher schon mal erklärt. Kurz gesagt nimmt man mehrere kleine Teleskope und schaltet sie so zusammen, dass sie wie ein viel größeres Teleskop funktionieren. Das ist in der Realität natürlich komplizierter als es klingt und funktioniert nicht in allen Fällen. Bei den Teleskopen der Europäischen Südsternwarte funktioniert es allerdings. Mit so einem Teleskop kann man dann zwar keine “Bilder” im klassischen Sinn mehr machen. Aber man kann wunderbar Daten sammeln und genau das haben die Leute von GRAVITY getan.
Sie haben vor allem nach Strahlung im Infrarotbereich des Lichtspektrums gesucht. Die entsteht in der Umgebung des schwarzen Lochs wenn dort etwa Elektronen sehr schnell beschleunigt werden. Und “schnell” meint hier bis zu 30 Prozent der Lichtgeschwindigkeit. Vereinfacht gesagt: Wenn Zeug im innersten Bereich der großen Scheibe um das schwarze Loch extrem schnell beschleunigt wird, dann gibt es “Flares”, also Helligkeitsausbrüche. Und genau so etwas hat GRAVITY beobachtet und zwar am 27. Mai 2018, dem 22 .Juli 2018 und dem 28. Juli 2018 (Hey – mein Geburtstag!).

Noch eine (andere) COMPUTERSIMULATION (!!!) mit Umlaufbahnen von Sternen um das zentrale schwarze Loch der Milchstraße. (Bild: ESO/L. Calçada/spaceengine.org)
Aus den Daten der Flares konnten die Forscher die Bewegung des Materials nachvollziehen, das sie verursacht hat. Und diese Bewegung hat, so zeigt die Analyse, hat ziemlich genau am innersten Rand des Ereignishorizonts stattgefunden. Also genau die Grenze, hinter der sich das befindet, was wir “schwarzes Loch” nennen. Was den Ereignishorizont überschreitet, kann nicht mehr zurück; genau dort fängt all das an, was an den schwarzen Löchern so seltsam ist.
Die Größe und die Eigenschaften des schwarzen Lochs, die man aus den Flares ableiten kann, stimmen in allen drei Fällen überein (und noch dazu mit den bestehenden Daten die wir von S2 haben). Mit den Daten von GRAVITY kann man nun eigentlich ohne jeden Zweifel feststellen: Jawohl, das Ding im Zentrum unserer Milchstraße IST EIN SCHWARZES LOCH! Und wie immer bei ersten Beobachtungen: Bald wird es zweite, dritte und vierte Beobachtungen geben. Wir werden noch mehr Daten sammeln; wir werden immer besser zusehen können, wie Zeug mit relativistischen Geschwindigkeiten um das supermassereiche schwarze Loch im Zentrum der Milchstraße kreist. Und auch wenn das schon beeindruckend genug ist, werden wir dadurch auch das Loch selbst immer besser verstehen.











Kommentare (50)