 Das ist die Transkription einer Folge meines Sternengeschichten-Podcasts. Die Folge gibt es auch als MP3-Download und YouTube-Video. Und den ganzen Podcast findet ihr auch bei Spotify.
Das ist die Transkription einer Folge meines Sternengeschichten-Podcasts. Die Folge gibt es auch als MP3-Download und YouTube-Video. Und den ganzen Podcast findet ihr auch bei Spotify.
Mehr Informationen: [Podcast-Feed][iTunes][Bitlove][Facebook] [Twitter]
Wer den Podcast finanziell unterstützen möchte, kann das hier tun: Mit PayPal, Patreon oder Steady.
Über Bewertungen und Kommentare freue ich mich auf allen Kanälen.
————————————————–
Sternengeschichten Folge 476: Parkplätze im All: Wo sind die Lagrange-Punkte?
Wir haben im Laufe der Zeit jede Menge Sachen ins All geschickt. Satelliten, Raumschiffe, Sonden, Weltraumteleskope, und so weiter. Das Problem an der Sache – oder besser gesagt eines der vielen, vielen Probleme die man bei der Raumfahrt hat: Im Weltall steht nichts still. Wir wollen einen Satelliten zum Beispiel ja nicht einfach nur mit einer Rakete ins All schicken. Der soll dann dort ja auch ganz konkrete Aufgaben erledigen. Da hilft es nicht, wenn er auf Nimmerwiedersehen in den Tiefen des Kosmos verschwindet. Oder gleich wieder runter auf die Erde fällt. Wir schicken Objekte ins All damit sie dort ganz bestimmte Dinge an ganz bestimmten Orten erledigen. Nur kann man eben im Weltraum nicht einfach irgendwo hin fliegen und dort dann einfach stehen bleiben. Das geht nicht. Oder besser gesagt: Es geht nicht auf die Art und Weise wie wir das vom Erdboden kennen.
Was man auf jeden Fall tun kann: Irgendwas umkreisen. Satelliten die die Erde beobachten, umkreisen die Erde. Satelliten, die den Mars erforschen sollen, umkreisen den Mars. Die Umlaufbahn um einen Himmelskörper herum ist quasi ein “stehen bleiben”. Was aber, wenn man nicht an der Erforschung eines Planeten oder Mondes interessiert ist? Sondern zum Beispiel ein Weltraumteleskop hat, das überall am Himmel Beobachtungen anstellen soll? Auch das muss ja irgendwo sein und man kann es zum Beispiel einfach auch in eine Umlaufbahn um die Erde parken. Das ist praktisch, weil es dann vergleichsweise nahe ist. Man braucht nicht so viel Treibstoff, um in eine nahe Erdumlaufbahn zu gelangen. Es kann aber auch sein, dass dann die Erde gerade im Weg steht, wenn man was beobachten will. Oder dass Streulicht von der Erde die Beobachtungen stört. Viele Satelliten und Teleskope müssen daher weit weg von der Erde sein. Kein Problem, kann man sich dann ja denken. Dann soll das Ding eben einfach direkt die Sonne umkreisen; machen die ganzen Planeten ja auch.
Und das ist natürlich möglich. Man braucht zwar ein bisschen mehr Energie und Treibstoff, um ein Objekt in einer heliozentrischen Bahn, also einer Umlaufbahn um die Sonne zu platzieren. Aber wenn es einmal dort ist, braucht man nicht mehr viel tun. Dann bewegt sich das Ding um die Sonne herum und fertig. Es gibt aber ein paar Punkte im Weltall, die besonders gut für Beobachtungen geeignet sind. Das sind die sogenannten “Lagrange-Punkte”, von denen ich in Folge 31 der Sternengeschichten schon ausführlich gesprochen habe. Das ist aber schon eine Zeit lang her, also fasse ich das noch einmal kurz zusammen.
Betrachten wir zwei Himmelskörper, zum Beispiel die Sonne und die Erde. Die Sonne übt eine Gravitationskraft aus und die Erde ebenso. Wir ignorieren jetzt fürs erste mal die restlichen Planeten und Monde im Sonnensystem und stellen uns vor, dass wir nur Sonne und Erde haben. Und ein drittes Objekt, eine sogenannte “Testmasse”. Die ist vernachlässigbar klein im Vergleich zur Masse von Erde und Sonne. Und dient uns einfach nur dazu, um zu “testen”, wie stark die gesamt wirkenden Gravitationskräfte sind. Wir stellen diese Testmasse also gedanklich einfach irgendwo im Sonnensystem ab und schauen, wie die Gravitationskräfte von Sonne und Erde auf sie wirken und welche Bewegung der Testmasse daraus entsteht.
In der Praxis macht man so eine Untersuchung natürlich mathematisch und es ist auch ein wenig komplizierter als ich das beschreibe. Aber schon im 18. Jahrhundert hat man genau solche Berechnungen angestellt und dabei fünf ganz besondere Punkte gefunden. Man könnte ja denken, dass es nur zwei prinzipielle Möglichkeiten gibt: Entweder unsere Testmasse umkreist direkt die Sonne. Oder sie umkreist die Erde (und mit der Erde gemeinsam um die Sonne). Gut, sie könnte auch mit Erde oder Sonne zusammenstoßen oder in den interstellaren Raum hinaus fliegen. Aber das ignorieren wir jetzt mal und bleiben bei den stabilen Umlaufbahnen. Und tatsächlich wird die Testmasse die Erde umkreisen, wenn wir sie ausreichend nahe an der Erde platzieren. Ist sie zu weit weg, dann ist die Anziehungskraft der Sonne zu stark und sie wird sich auf einer heliozentrischen Umlaufbahn wiederfinden. Aber theoretisch muss es irgendwo dazwischen ja einen Punkt geben, an dem die Sonne mit ihrer Gravitationskraft genau so stark an der Testmasse zieht wie die Erde? Was würde dort passieren?
Bei der Antwort auf diese Frage landen wir exakt bei den Lagrange-Punkten, die nach dem Mathematiker Joseph Louis Lagrange benannt sind, der dieses Problem im 18. Jahrhundert untersucht hat. Es ist ein bisschen knifflig; denn wenn man sich die Sache überlegt, dann merkt man, dass es nicht einen solchen Punkt gibt, sondern gleich fünf davon.
Stellen wir uns vor, wir befinden uns mit unserer Testmasse irgendwo auf der Verbindungslinie zwischen Erde und Sonne, zwischen den beiden Himmelskörpern. Je näher an der Sonne, desto stärker ist deren Anziehungskraft und desto schneller umkreist die Testmasse die Sonne auch. Die Erde zieht aber eben auch immer ein bisschen und aus Sicht der Testmasse wirkt das so, als wäre die Anziehungskraft der Sonne ein klein wenig schwächer als sie es tatsächlich ist. Normalerweise wäre ein Objekt das sich innerhalb der Erdbahn bewegt immer schneller als die Erde. Aber wegen der Anziehungskraft der Erde gibt es einen Punkt, an dem sich die Testmesse innerhalb der Erdbahn befindet und trotzdem genau so schnell wie die Erde um die Sonne läuft. Das ist ein Lagrange-Punkt und zwar der Lagrange-Punkt mit der Bezeichnung L1. Und die Bezeichnung “Punkt” kann ein wenig irreführend sein. Denn wie gesagt: Im All bewegt sich alles. Die Erde bewegt sich um die Sonne; man kann sich die Verbindungslinie zwischen Erde und Sonne wie den Zeiger einer Uhr vorstellen der eine Runde pro Jahr absolviert. Und da der Punkt L1 immer exakt auf diesem Zeiger, auf der Verbindungslinie liegen muss, bewegt sich auch der Punkt um die Sonne herum. Gemeinsam mit der Erde und genau so schnell wie sie. Der Lagrange-Punkt L1 ist also ständig in Bewegung, genau so wie der Rest im Weltall.
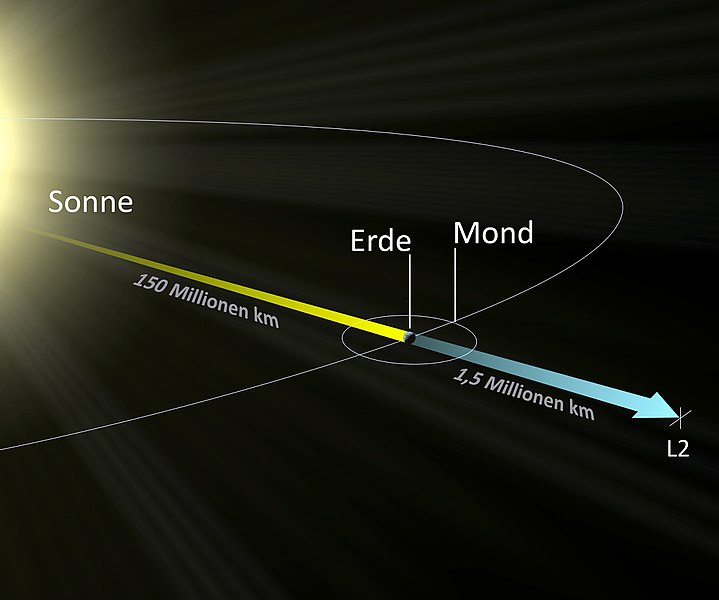
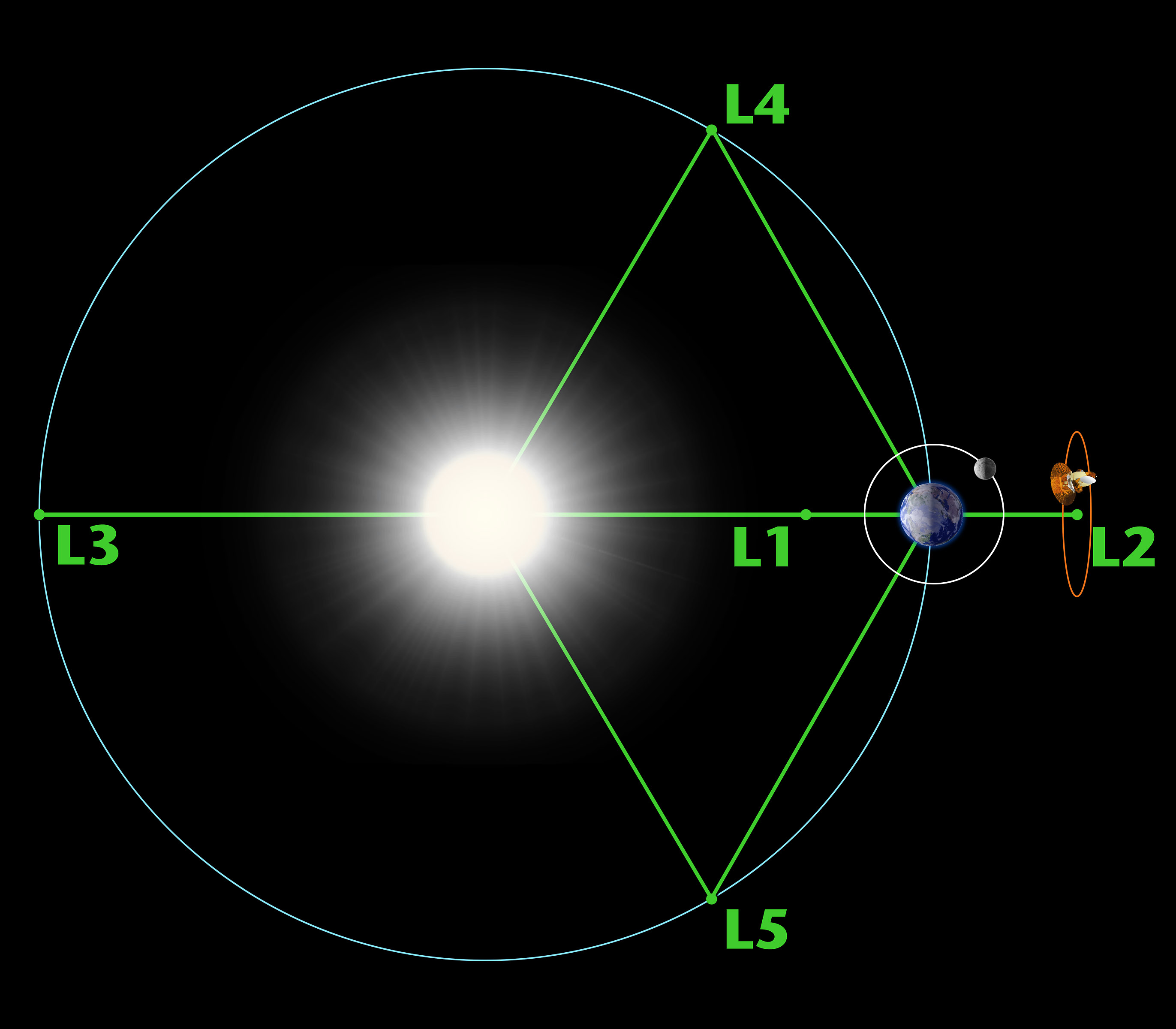
Warum es einen Gleichgewichtspunkt zwischen Erde und Sonne geben muss, ist vergleichsweise klar. Aber wenn wir nun die Verbindungslinie über die Erdbahn hinaus verlängern, finden wir noch zwei weitere Gleichgewichtspunkte. Wenn sich die Testmasse außerhalb der Erdumlaufbahn befindet, dann sollte sie sich eigentlich immer langsamer um die Sonne bewegen als die Erde. Da ist die Anziehungskraft der Sonne auf die Testmasse ja schwächer als die Anziehungskraft der Sonne auf die Erde. Aber nicht vergessen: Wir betrachten ja die Positionen entlang der Verbindungslinie Erde-Sonne. Das heißt dort ziehen Sonne und Erde gleichzeitig in die gleiche Richtung. Aus Sicht der Testmasse ist die Anziehungskraft also immer ein klein wenig stärker als sie eigentlich sein sollte und deswegen gibt es auch hier einen Punkt, an dem sie sich nicht langsamer, sondern genau so schnell wie die Erde um die Sonne bewegt. Das ist der Lagrange-Punkt L2 und den dritten Punkt finden wir, wenn wir in die andere Richtung schauen. Wir setzen die Testmasse jetzt nicht hinter die Erde, sondern gegenüber der Erde auf die andere Seite der Sonne. Ohne Bilder ist das ein wenig schwierig vorzustellen. Aber es ist eigentlich ganz simpel. Bei L1 lautet die Reihenfolge der Objekte entlang der Linie: Sonne – L1 – Erde. Bei L2 ist es: Sonne – Erde – L2. Und jetzt schauen wir uns an, wie es bei der Reihung: L3 – Sonne – Erde ausschaut. Hier passiert das gleiche wie bei L2. Sonne und Erde ziehen die Testmasse in die gleiche Richtung, weswegen wie sie ein wenig schneller unterwegs ist als normal und deswegen gibt es auch hier – eben in L3 – einen Punkt, an dem sich die Testmasse genau so schnell bewegt wie die Erde.
Bis jetzt haben wir uns nur entlang der Verbindungslinie zwischen Sonne und Erde bewegt. Es gibt aber noch zwei weitere Punkte, an denen die Testmasse ein Gleichgewicht der Kräfte spürt. Wir schieben unsere Testmasse jetzt direkt die Erdumlaufbahn entlang. Wer eine gute Vorstellungskraft hat, kann jetzt ein Dreieck vor dem inneren Auge entstehen lassen. Dessen Eckpunkte sind die Sonne, die Erde und die Testmasse. Wenn die Testmasse noch ganz in der Nähe der Erde ist, dann ist Dreick lang und flach. Der Abstand der Erde zur Sonne ist zwar immer genau so groß wie der Abstand der Testmasse zur Sonne. Die Distanz zwischen Erde und Testmasse ist aber viel kleiner. Wir haben also ein gleichschenkeliges Dreieck mit zwei langen und gleich langen Seiten und einer sehr kurzen. Je weiter wir die Testmasse aber entlang der Erdumlaufbahn schieben, desto länger wird diese dritte Seite. Bis wir irgendwann ein gleichseitiges Dreieck erhalten! Jetzt ist der Abstand zwischen Sonne und Erde genau so groß wie der zwischen Sonne und Testmasse und Erde und Testmasse. Wir können sogar zwei solcher gleichseitigen Dreiecke basteln; einmal wenn sich die Testmasse genau 60 Grad vor der Erde entlang ihrer Bahn befindet und einmal 60 Grad hinter der Erde. Das sind die beiden noch fehlenden Lagrange-Punkte L4 und L4. Und das schaut jetzt zwar schön symmetrisch aus. Aber wieso sollen L4 und L5 auch Gleichgewichtspunkte sein? Wenn der Abstand zwischen Erde und Testmasse und Sonne und Testmasse genau gleich groß ist, dann folgt daraus ja nicht, dass Sonne und Erde auch genau gleich stark an der Testmasse ziehen? Die Sonne hat viel mehr Masse und bei gleichem Abstand muss ihre Anziehungskraft auch immer sehr viel größer sein als die der Erde.
Wenn man wirklich verstehen will was hier abgeht, kommt man nicht ohne sehr viel Mathematik aus. Und muss vor allem ein weiteres Mal berücksichtigen, dass man es mit einer dynamischen Situation zu tun hat; sich also alles bewegt. Ich probiere es mal mit einer sehr vereinfachten Erklärung, die ohne Mathematik auskommt. Im Prinzip geht es ja darum, wie viel Bewegungsenergie die Testmasse braucht, damit sie sich immer genau so schnell wie die Erde um die Sonne herum bewegen kann. Nur wenn das der Fall ist, dann bleibt sie auch immer vor der Erde (bzw. hinter ihr) auf ihrer Bahn in der gleichen Position. Wir wollen eine Konfiguration von Sonne, Erde und Testmasse, in der die relative Position der drei Objekte immer exakt gleich bleibt. Alles dreht sich zwar um die Sonne, aber wenn wir uns selbst mit der Erde (oder der Testmasse) mitbewegen, dann würde es so aussehen, als würde sich gar nix bewegen. Von der Erde aus gesehen wäre die Testmasse in L4 immer genau gleich weit voraus und die in L5 gleich weit hintennach. Es sähe so aus, als würde sie sich gar nicht bewegen.
Und jetzt verlassen wir kurz den Weltraum und begeben uns auf die Erde. Die Erde dreht sich um ihre Achse, einmal in 24 Stunden. Wenn ich direkt am Äqutor stehe, dann dreht mich die Erdrotation also in 24 Stunden einmal herum. Und ich lege dabei eine Strecke zurück, die der Länge des Äquators entspricht, was circa 40.000 Kilometer sind. 40.000 Kilometer in 24 Stunden sind 1700 Kilometer pro Stunde und das ist die Geschwindigkeit mit der ich mich dank der Erdrotation bewege, auch wenn ich die ganze Zeit nur faul im Liegestuhl sitze. Wenn ich mich aber zum Beispiel in Berlin befinde, bin ich langsamer. Auch hier trägt mich die Erdrotation einmal in 24 Stunden im Kreis herum. Nur ist dieser Kreis jetzt viel kleiner. Wenn ich die Erde genau am Äquator in zwei Hälften schneiden würde, dann ist die Schnittfläche ein Kreis mit einem Umfang von den vorhin erwähnten 40.000 Kilometern. Wenn ich die Erde aber auf der Höhe von Berlin kappe, so wie morgens das Frühstücksei, dann kriege ich eine Schnittfläche die nur noch einen Umfang von 24.700 Kilometer hat. Meine Geschwindigkeit beträgt hier also 24.700 km pro 24 Stunden oder knapp 1000 km/h. Und noch weiter im Norden würde ich mich noch langsamer mit der Erde bewegen.
Keine Sorge, das hat alles mit den Lagrange-Punkten zu tun; da kommen wir gleich wieder drauf. Zuerst aber noch einmal kurz zum Wetter. Luftmassen bewegen sich ja einerseits mit der Erdrotation, genau so wie alles andere auf unserem Planeten. Andererseits können die Luftmassen aber um den Planeten herumströmen und sie tun das aufgrund von Unterschieden im Luftdruck. Stellen wir uns jetzt also mal Luft vor, die vom Äquator in Richtung Norden strömt. Am Äquator war sie mit den 1700 km/h unterwegs die sie dank der Erdrotation hat. Wenn sie jetzt aber nach Norden kommt, dann bewegt sie sich schneller nach Osten (die Erde dreht sich nach Osten) als das Land unter ihr, dass sich im Norden ja langsamer dreht. Vom Erdboden betrachtet sieht das so aus, als würde die aus Süden kommende strömende Luft nach Osten abgelenkt. In die andere Richtung geht das natürlich auch: Luft die von Richtung Norden kommt, wird nach Westen abgelenkt. Wenn nun Luft aus allen Richtungen auf ein Tiefdruckgebiet zuströmt, dann bildet sich ein Luftwirbel, der sich gegen den Uhrzeigersinn dreht (und auf der Südhalbkugel ist das alles umgekehrt). So entstehen die großen Wettermuster, so entstehen Hurrikane und so weiter. Die Kraft, die die Luft zum Wirbeln bringt, heißt “Corioliskraft” und sie ist nur eine Scheinkraft. Soll heißen: Da ist nicht wirklich irgendwas, was von außen an der Luft drückt und eine reale Kraft ausübt. Die Corioliskraft gibt es, weil Objekte – wie eben Luft – träge sind und weil wir uns in einem rotierenden Bezugssystem befinden. Wir drehen uns mit der Erde mit und nehmen die Rotation nicht direkt wahr. Wir sehen aber, wie sich die Rotation auf die trägen Luftmassen auswirkt und es sieht für uns so aus wie eine Kraft, die dort wirkt.
Und damit sind wir wieder zurück im Weltall und bei den Lagrange-Punkten. Auch hier haben wir es mit einem rotierenden Bezugssystem zu tun. Wir betrachten die Dinge ja aus einer Position, in der wir uns mit der Erde um die Sonne bewegen (oder mit der Testmasse, das ist egal). Und auch hier spielt die Corioliskraft eine Rolle. In einem gewissen Abstand von der Sonne spürt man eine gewissen Anziehungskraft und die sorgt für eine gewisse Geschwindigkeit, genau so, dass das man am Ende die Sonne umkreist. Weiter weg von der Sonne ist diese Geschwindigkeit geringer als näher dran; genau das ist übrigens das, was das dritte Keplersche Gesetz besagt. So wie die Luftmassen auf der Erde unterschiedlich schnell sind, je nachdem ob sie nah oder weit weg vom Äquator sind, ist das auch bei der Bewegung von Objekten um die Sonne. Ich könnte jetzt sagen: Und so wie die Luftmassen dank der Corioliskraft um das Tiefdruckgebiet wirbeln, bewegen sich Objekte dank der Corioliskraft um die Lagrange-Punkte L4 und L5 herum. Aber dann hätte ich die Analogie zu weit geführt; so simpel ist es nicht, leider. Aber wenn man sich vorstellt, dass ein Objekt ein klein wenig aus L4 oder L5 herausgeschubst wird, näher an die Sonne heran oder weiter von ihr weg, dann ist klar, dass es dann – vorerst – zu schnell oder zu langsam ist für den Abstand den es zur Sonne hat. Das wird dazu führen, dass es sich näher an die Sonne bewegt oder weiter weg, quasi als Korrektur. Dann wird es aber nicht mehr exakt in L4 oder L5 landen sondern wieder ein bisschen zu nah oder zu fern sein; diesmal eben andersherum. Was wieder zu einer Korrektur führt, und so weiter. Am Ende kriegt man eine Bewegung UM den Lagrange-Punkt herum.

Corioliskraft (Bild: NASA
Man kann die ganzen Kräfte – die Gravitationskräfte von Sonne und Erde nehmen, die Corioliskraft und die Zentrifugalkräfte muss man eigentlich auch noch mitnehmen – und dann jede Menge Mathematik draufwerfen. Und am Ende wird man sehen, dass die Gleichgewichtspunkte sich eben genau dort befinden, wo Sonne, Erde und Testmasse ein gleichseitiges Dreieck bilden. Noch genauer kann man es ohne Formeln vermutlich nicht erklären. Es gibt noch diverse Einschränkungen; eine der beiden Massen muss zum Beispiel immer sehr viel größer sein als die andere, sonst können L4 und L5 keine stabilen Gleichgewichtspunkte sein, und so weiter. Aber wir sind eh schon zu tief in die mathematischen Details eingetaucht für eine Podcastfolge.
Jetzt wissen wir also genau, wo die Lagrange-Punkte sind und auch so ungefähr, warum sie dort sind, wo sie sind. Jetzt müssen wir noch wissen, wie man dort ein Raumfahrzeug parkt. Aber das schauen wir uns dann in der nächsten Folge an.












Kommentare (19)