Es gibt keine Schwerkraft, sondern nur die Raumzeitkrümmung – das haben wir im letzten Teil gesehen. Deshalb lohnt es sich, zum Abschluss noch einmal einen Blick auf die Raumzeitkrümmung zu werfen, also auf die Metrik.
Ihr erinnert euch noch an Teil II und Teil III? Dort haben wir gesehen, dass Geodäten zeigen, ob ein Raum gekrümmt ist: Laufen zwei Geodäten immer aufeinander zu, dann ist die Krümmung positiv, laufen sie voneinander weg, dann ist sie negativ.
Geodäten über der Erde
Geodäten in der Raumzeit sind die Weltlinien von Teilchen, die kräftefrei sind (dran denken: Schwerkraft gibt es nicht) und nur der Raumzeitkrümmung folgen. Als erstes lassen wir drei Teilchen in einer Erdumlaufbahn starten, die alle den gleichen Abstand von der Erde haben. Die Anfangsgeschwindigkeit der Teilchen ist Null, sie fallen also einfach auf die Erde zu (Bild zum Vergrößern anklicken):
Dabei habe ich die Erde zweidimensional gezeichnet, damit ich die dritte Dimension für die Zeit nehmen kann. Ich habe ein Koordinatensystem mit Ursprung im Zentrum der Erde mitgezeichnet; das wird später noch hilfreich werden. Ein Wort der Warnung: Dieses und die folgenden Bilder sind nicht maßstabsgetreu.
Was passiert mit unseren Teilchen? Sie beschleunigen auf die Erde zu, und zwar alle um denselben Betrag. Weil sie von Außen kommen, nähern sie sich dabei einander an. In dieser Richtung ist die Raumzeit also positiv gekrümmt.
Als nächstes starten wir die drei Teilchen mit unterschiedlicher Entfernung zur Erde. Das nächste Teilchen wird, weil es dichter an der Erde ist, stärker beschleunigt, das am weitesten entfernte Teilchen am wenigsten. Entsprechend laufen die Geodäten auseinander:
Die Raumzeit hat also auch einen negativen Krümmungsanteil.
Man kann beide Bilder zusammenfassen, indem man sich anschaut, was aus einem Kreis aus Teilchen wird: Der wird in der einen Richtung gelängt, in der anderen gestaucht:
Wenn der Kreis ein materielles Objekt wäre, dann würde er sich also verformen. Für den Kreis würde es so aussehen, als würde die Seite, die näher zur Erde ist, stärker angezogen, die Seite, die am weitesten weg ist, schwächer. Kommt euch sowas bekannt vor? Richtig, wir haben gerade die Gezeiten wiederentdeckt (bei denen ist es natürlich die Erde, deren Ozeane in der Raumkrümmung des Mondes verzerrt werden):
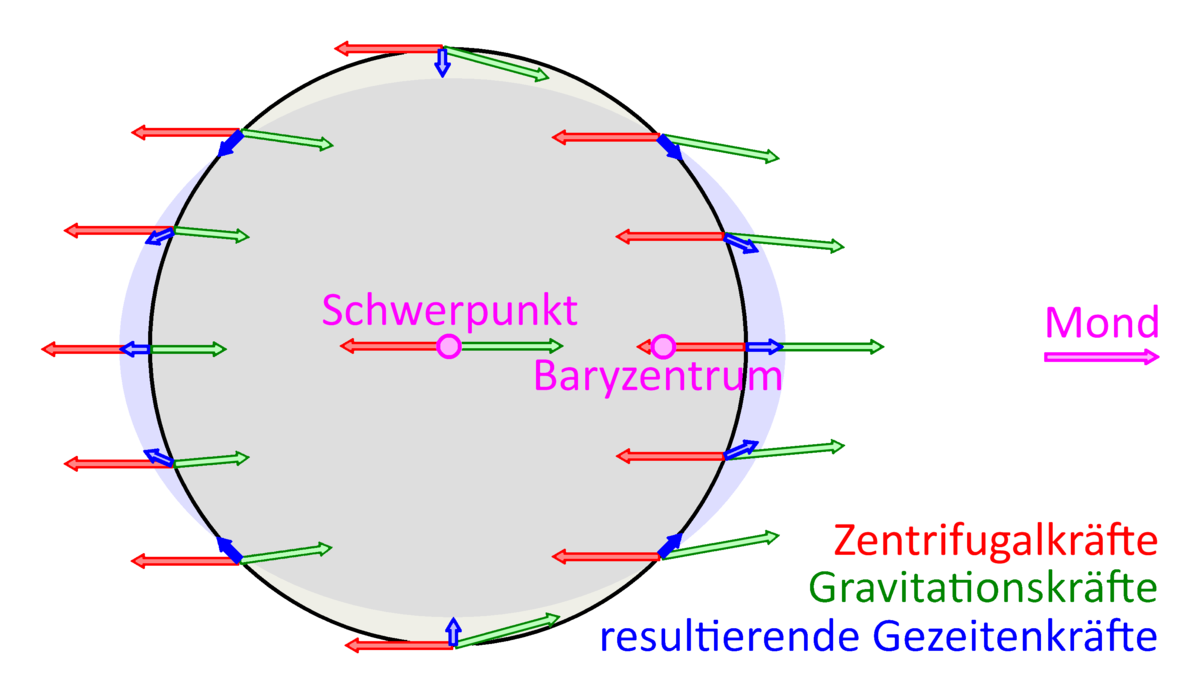
Von de:Benutzer:Dringend, bearbeitet von Lämpel – eigene Skizze, CC BY-SA 3.0 de, Link
Bild wie immer von Wikipedia [hier war früher ein anderes bild, das hatte aber Copyrightprobleme…] – allerdings dort ganz klassisch mit “Kräften” erklärt, statt richtig mit der Raumzeitkrümmung. Die Raumzeitkrümmung erklärt auch vollkommen zwanglos und stressfrei, warum es zwei Flutberge geben muss – der Kreis wird zur Ellipse verzerrt, nicht zu einem Ei.
Letztes Mal hatte ich ja behauptet, dass man ein “Schwerefeld” und eine Beschleunigung in einer Rakete nicht voneinander unterscheiden kann. Das gilt allerdings nur, wenn man ein sehr kleines Labor hat – wenn das Labor groß genug ist, dann könnte man Gezeiteneffekte sehen, die es in einer beschleunigten Rakete nicht gibt. (Das ist allerdings kein Widerspruch zum Äquivalenzprinzip – man kann sich nämlich auch ein vollkommen homogenes Schwerefeld über einer massiven Platte vorstellen, bei dem gibt es keine Gezeiten.)
Gezeiteneffekte machen es also möglich, die Krümmung der Raumzeit sichtbar zu machen. Unser Kreis wird beispielsweise zur Ellipse verzerrt. Da er in einer Richtung länger, in der anderen kürzer wird, können wir sehen, dass die mittlere Krümmung der Raumzeit gerade gleich Null ist. Das muss auch so sein, denn eine nicht verschwindende mittlere Krümmung der Raumzeit gibt es nur da, wo Materie ist (also beispielsweise im Inneren der Erde).
Die Raumkrümmung im Erdinnern
Die Bilder von oben gelten außerhalb der Erde. Im Erdinnern sieht die Raumkrümmung anders aus. (Ich nehme hier der Einfachheit halber an, dass die Erde eine perfekte Kugel mit konstanter Dichte ist.)
Am leichtesten kann man das, was passiert, jetzt doch wieder mit dem einfachen Bild der “Schwerkraft” einsehen, weil es uns vertrauter ist als die Raumzeitkrümmung. Genau im Mittelpunkt der Erde wäre man ja “schwerelos” – jede “Schwerkraft” wirkt nach außen in alle Richtungen gleichmäßig, so dass sich alle Kräfte aufheben. (Wegen der Symmetrie kann eine Geodäte nicht aus der Mitte herausführen, denn alle Richtungen sind gleich.)
Für einen Punkt weiter außen ist immer nur der Anteil der Erdmasse relevant, der innerhalb einer Kugel liegt, die die aktuelle Entfernung vom Erdmittelpunkt als Radius hat, Anteile, die von weiter außen kommen, heben sich auf. (Das zu beweisen ist eine beliebte Aufgabe für Physikstudis im 1. oder 2. Semester, an der kommt niemand vorbei.) Die “Schwerkraft” nimmt also nach innen hin immer weiter ab. Wenn wir wieder das Spiel von eben spielen und drei Teilchen loslassen, dann laufen diese, wenn sie alle denselben Abstand vom Erdmittelpunkt haben, natürlich aufeinander zu. (Ich mache von meinem Recht als Theoretiker Gebrauch, solche Trivialitäten wie die Tatsache, dass Teilchen schlecht störungsfrei durch das Erdinnere fliegen können, zu vernachlässigen.)
Starten wir drei Teilchen mit jeweils unterschiedlichem Abstand vom Erdinnern, so wird das äußerste jetzt stärker beschleunigt als das innerste, weil es ja mehr Masse “sieht”. Entsprechend bekommt es eine höhere Geschwindigkeit, so dass auch hier die Teilchen aufeinander zulaufen. Anders als außerhalb der Erde ist die Raumzeitkümmung hier also positiv, alle Geodäten laufen im Erdinnern aufeinander zu.
Die Metrik im Innern der Erde sieht also anders aus – der “Überschussradius” aus dem zweiten Teil wird im Innern der Erde wieder kleiner, weil immer weniger Masse in den gezeichneten Kreis eingeschlossen wird, die den Raum krümmt. Der “Überschussradius” ist also im Zentrum der Erde Null, nimmt dann stetig zu, bis er an der Erdoberfläche einen Maximalwert erreicht. Gehen wir weiter nach Außen, so nimmt er dann wieder ab. Der Abstand zwischen zwei Koordinatenlinien auf einer Karte (die wir gleich angucken) verhält sich also mit zunehmendem Abstand vom Erdmittelpunkt so:
Das zeichnen wir jetzt in eine Karte ein. Dabei verwenden wir einen zweidimensionaler Schnitt durch die Raumzeit, bei dem die Zeit konstant gehalten wird. Als Variablen nehmen wir einmal den Winkel (das ist einfach) und als radiale Koordinate den Umfang eines Kreises geteilt durch 2π. (Sogenannte Schwarzschild-Koordinaten.) Der Abstand zwischen zwei Koordinatenlinien nimmt dann, wie eben gesehen, im Innern zu, nach außen hin wieder ab.
Das Ergebnis sieht so aus:
Eventuell müsst ihr draufklicken, um die unterschiedliche Größe der roten Linien, die die Strecke nach Außen hin angeben, erkennen zu können. Dass die grünen Linien immer länger werden, hat nichts mit der Raumkrümmung zu tun, sondern liegt daran, dass wir hier Winkelkoordinaten (sogenannte Polarkoordinaten) verwenden – so wie bei einer Schallplatte (falls noch einer weiß, was das ist) der Außenrand eine größere Strecke zurücklegen muss als ein Punkt weiter innen, wenn sich die Platte dreht, so ist es auch bei der Winkelkoordinate.
Die Längenänderung der nach außen zeigenden (radialen) Koordinate hat aber tatsächlich etwas mit der Raumkrümmung zu tun – in der Ebene wäre diese Länge immer gleich. Falls es euch ärgert, dass man die unterschiedlichen Längen im Bild nicht so gut sieht – es liegt daran, dass dies keine schematische Darstellung ist, sondern eine, in der die Längen tatsächlich aus den Formeln der ART berechnet sind. (Allerdings nicht für die Erde, sondern für einen Stern mit extrem hoher Dichte, sonst würde man gar nichts erkennen.)
 Um genau zu sein, falls es jemand wissen will: In Einheiten von c=G=1 habe ich einen Radius von 0.1 und eine Masse von 0.02 angesetzt und dann die Gleichung für die Schwarzschildmetrik benutzt (wobei man jeweils die Wurzel aus dem Term für den metrischen Tensor ziehen muss). Die Formeln habe ich in gnuplot eingetippt. (Im Plot des Abstands gegen den Radius habe ich dann den Radius auf 1 umnormiert.)
Um genau zu sein, falls es jemand wissen will: In Einheiten von c=G=1 habe ich einen Radius von 0.1 und eine Masse von 0.02 angesetzt und dann die Gleichung für die Schwarzschildmetrik benutzt (wobei man jeweils die Wurzel aus dem Term für den metrischen Tensor ziehen muss). Die Formeln habe ich in gnuplot eingetippt. (Im Plot des Abstands gegen den Radius habe ich dann den Radius auf 1 umnormiert.)
Das Gummituch-Modell
Die Raumkrümmung wird ja gern mit “Gummituch-Modellen” veranschaulicht, in denen der gekrümmte Raum als zweidimensionale Fläche im dreidimensionalen Raum dargestellt wird. Das sieht meist etwa so aus:
Häufig wird dazu gesagt, dass man sich den Raum eben als “Gummituch” vorstellen soll, in dem die Massen Vertiefungen erzeugen. Das ist natürlich gleich mehrfach unsinnig: Die dritte Dimension in diesem Gummituchbild hat ja keine physikalische Bedeutung. Außerdem – damit die Massen eine Vertiefung erzeugen könnten, müsste es ja eine Schwerkraft in der dritten Dimension geben, die “nach unten” wirkt. Es wäre ziemlich blödsinnig, die Schwerkraft über die Schwerkraft erklären zu wollen…
Trotz dieser Probleme können solche Bilder der Anschauung für den gekrümmten Raum manchmal helfen. Wenn ihr euch vorstellen wollt, wie man ein solches Bild “korrekt” erzeugen kann, dann geht das so: Stellt euch ein flaches Koordinatennetz vor, bei dem die einzelnen “Knoten” mit Stäben verbunden sind, so wie in meinem Bild oben. Jetzt dehnt oder staucht ihr die Abstände zwischen den Koordinatenlinien entsprechend der Metrik. Außerhalb der Erdkugel oben im Bild werden die Stäbe um so länger, je weiter man nach innen kommt, deshalb wölbt sich das Netz trichterförmig auf. Im Innern der Erde werden die Stäbe wieder kürzer, das Netz biegt sich also wieder zurück. Was wir hier sehen, ist analog zu den gestrickten hyperbolischen Räumen, die ich neulich gezeigt habe – wenn die Strickmaschen von Länge und Umfang her nicht zueinander passen, dann verwirft sich das Gestrickte zu einem dreidimensionalen Objekt.
Hier noch einmal ein Bild “von der Seite”, bei dem man den positiv (wie eine Kugel) gekrümmten Bereich im Zentrum besser sieht:
 Auch dieses Bild habe ich mit gnuplot gemacht. Die Formeln dazu habe ich aus dem Misner, Thorne, Wheeler, Kap. 23. Allerdings gibt es da etwas, das mir Kopfzerbrechen bereitet – vielleicht ist ja jemand von euch schlauer als ich? Die Formel für die z-Koordinate lautet im MTW (23.34b)
Auch dieses Bild habe ich mit gnuplot gemacht. Die Formeln dazu habe ich aus dem Misner, Thorne, Wheeler, Kap. 23. Allerdings gibt es da etwas, das mir Kopfzerbrechen bereitet – vielleicht ist ja jemand von euch schlauer als ich? Die Formel für die z-Koordinate lautet im MTW (23.34b)
z(r) = √[8M (r-2M)]
Für große r verhält sich das wie √r. Die Gumifläche sollte also auch weit außen immer noch gekrümmt sein. Auch im Text steht, dass die Fläche asymptotisch nach außen niemals flach wird außer bei unendlicher Entfernung. Das zugehörige Bild 23.1 (wie auch alle anderen typischen Gummituch-Bilder, die man zu sehen bekommt), wird aber nach Außen hin flach:
Falls jemand mir erklären kann, woher die Diskrepanz kommt, wäre das super. Vielleicht ist es tatsächlich nur eine inkorrekte Vereinfachung – jedenfalls habe ich hier eine Darstellung gefunden, die meiner entspricht. Auf der Seite gibt es übrigens auch ziemlich coole Animationen. (Dieser gut in einem Warn-Abschnitt versteckte link ist meine Version eines “easter eggs”)
Die Raumzeitmetrik
Ganz oben hatte ich ja Raumzeit-Diagramme gezeigt, dann habe ich euch die Metrik des Raumes veranschaulicht. Was jetzt noch fehlt, ist die Zeitkomponente der Metrik. Anders als bei der räumlichen Komponente, bei der ja der Überschussradius im Innern der Erde wieder abnimmt, vergeht die Zeit immer langsamer, je weiter man nach Innen kommt. Hier die entsprechende Grafik:
Wieder ist auf der x-Achse der Abstand vom Zentrum aufgetragen, auf der y-Achse jetzt der zeitliche Abstand zwischen zwei “Zeitkoordinaten” – im Bild ganz oben mit den Weltlinien also der zeitliche Abstand zwischen zwei Punkten in übereinanderliegenden Scheiben.
Man erkennt, dass die Zeit immer langsamer verläuft, je weiter man nach innen kommt. Auch außerhalb der Erde ist die Zeit entsprechend “verlangsamt” – wir hatten ja schon im letzten Teil gesehen, dass das dafür verantwortlich ist, dass Bälle auf gekrümmten Bahnen fliegen, wenn man sie wirft.
Es wäre schön, wenn man die ganze Raumzeitkrümmung in einem Bild darstellen könnte. Dazu nehme ich die Netzdarstellung mit den roten und grünen Abstandslinien von oben und zeichne den zeitlichen Abstand aus dem Bild hier als dritte Dimension hinein. Damit man sieht, wie die Zeit vergeht, staple ich – wie ganz am Anfang – drei Bilder übereinander. Das Ergebnis ist ein bisschen unübersichtlich (zum Vergrößern anklicken) – das ist vermutlich auch der Grund, warum ich so ein Bild noch nie gesehen habe; außer mir scheint niemand diese Darstellung hilfreich zu finden (die macht übrigens auch ziemlich viel Arbeit…):
An den blauen Linien seht ihr, wie die zeit nach Außen hin “schneller” vergeht; die roten Linien zeigen den abnehmenden Abstand, je weiter man nach Außen geht. Ein vertikaler Schnitt durch das Ganze entspricht unserem zweidimensionalen Diagramm vom letzten Mal (dem mit der Nase) – man kann also auch an dieser dreidimensionalen Darstellung sehen, dass Geodäten gekrümmt sein müssen.
Wir verbiegen die Raumzeit noch weiter
Das Bild sieht schon ziemlich kompliziert aus – es ist aber immer noch vergleichsweise einfach. Die drei Linien in rot, blau und grün, die jeweils die Längen angeben, laufen ja immer genau in Richtung der Koordinatenlinien. Das muss aber nicht so sein. In komplizierteren Fällen ändert sich auch die “Orientierung” dieser Linien im Koordinatensystem ständig. Wenn also viele Massen wild umherwirbeln und vielleicht auch noch rotieren, kann das sehr unübersichtlich werden. Hier ein schwacher Versuch, das für einen Ausschnitt
darzustellen (allerdings in diesem Fall wirklich nur gezeichnet, nicht gerechnet):
 Falls jemand genau wissen will, was ich hier die ganze Zeit gezeichnet habe: Es ist nicht direkt die Metrik, sonder das sogenannte “Vierbein” (wobei eine Koordinate unterschlagen ist, deswegen sieht es aus wie ein Dreibein). Metrik und Vierbeinformalismus hängen sehr eng zusammen, wer näheres wissen will, kann in dieses Vorlesungsskript schauen.
Falls jemand genau wissen will, was ich hier die ganze Zeit gezeichnet habe: Es ist nicht direkt die Metrik, sonder das sogenannte “Vierbein” (wobei eine Koordinate unterschlagen ist, deswegen sieht es aus wie ein Dreibein). Metrik und Vierbeinformalismus hängen sehr eng zusammen, wer näheres wissen will, kann in dieses Vorlesungsskript schauen.
Beispielsweise verzerrt die Rotation der Erde das einfache “Gummituchmodell” von oben so, dass die nach außen laufenden Linien in Umfangsrichtung gekrümmt werden:
(Bild von der Stanford University)
Zu diesem Bild gibt es auch ein Video der Stanford University – auf deren homepage gibt es reichlich Material zum angucken. (Hallo Niels, danke für den Link.)
Mein schönes Raumzeitdiagramm von oben würde hier also noch komplizierter werden; und wenn man sich jetzt vielleicht noch zwei rotierende Sterne vorstellt, die aufeinander zufliegen, dann wird es richtig hübsch – aber das überlasse ich eurer Fantasie.
Ja, meine lieben Bullets und Basiliusse (Basilii!!), Nielse und Perks, Voynichs und Wapplers, Rolaks und Ronnies,
Dies war nun der sechste Teil dieser Serie, sechs Teile habe ich bis heute geschrieben.
Ich habe die Hälfte der Themen nicht halb so gut erklärt, wie ich es gerne würde, und ich verstehe weniger als die Hälfte der ART auch nur halb so gut, wie ich gern möchte. Aber ich bedaure kundtun zu müssen, dass dies – auch wenn sechs Teile viel zu wenig sind, um über die ART zu schreiben – das ENDE ist. Diese Serie ist zu Ende. JETZT.
Hier ein Überblick über die ganze Serie:
Wie man die Raumzeit krümmt. Teil I: Spielereien mit Landkarten
Wie man die Raumzeit krümmt. Teil II: Warum der Sonnenradius “zu groß” ist
Wie man die Raumzeit krümmt. Teil III Negative Krümmung und ein Tipp zum Pizza-Essen
Wie man die Raumzeit krümmt. Teil IV: Raumzeit – was ist das eigentlich?
Wie man die Raumzeit krümmt. Teil V Warum es keine Schwerkraft gibt






Kommentare (115)