Das Photon ist also sicher “da” – die Frage ist nur, wo zum Geier ist “da”?
(Man darf hier nicht den Fehler machen zu glauben, dass das Problem nur darin steckt, dass wir einfach nur nicht wissen, wo das Photon hingelaufen ist – der Überlagerungszustand ist tatsächlich real und mit geeigneten Experimenten lässt sich das auch nachweisen – hier ginge das dadurch, dass man die beiden Wege des Photons durch weitere Spiegel wieder zusammenführt und die Interferenz ausnutzt. Das will ich aber in diesem Text nicht erklären, hier soll es nur darum gehen, was wir wissen, nicht, wie wir es herausgefunden haben.)
2. Wo ist das Elektron?
Betrachten wir als nächstes ein Elektron. Wir schließen es in einem Kasten ein, so dass wir ganz sicher wissen, dass es drin ist. (Beispielsweise können wir seine elektrische Ladung messen.) Dann öffnen wir den Kasten, warten eine Weile, und schließen ihn wieder. Jetzt schauen wir nach, ob das Elektron immer noch drin ist – siehe da, das ist es. Es ist also sicherlich vernünftig anzunehmen, das Elektron wäre die ganze Zeit im Inneren des Kastens gewesen. Wir wiederholen das Experiment noch ein zweites, drittes und viertes Mal, immer mit demselben Ergebnis. Dann plötzlich, beim fünften Mal, ist der Kasten leer. Stattdessen spricht kurz danach unser Elektronendetektor an, den wir ein ganzes Stück weit weg vom Kasten aufgestellt haben.
Was ist da passiert? Warum war das Elektron vier Mal im Kasten und beim fünften Mal nicht, obwohl wir immer genau dasselbe getan haben?
Die Quantenmechanik gibt auf diese Frage zumindest eine Teilantwort: Ein Elektron ist normalerweise nicht an einem wohldefinierten Ort lokalisiert. Vielmehr hat es eine gewisse Wahrscheinlichkeit, dass man es an einem bestimmten Ort finden kann. (Bei unserem Photon war das genau so, da habe ich den Versuchsaufbau aber so gebastelt, dass es nur zwei Möglichkeiten hatte – auf dem Weg nach A oder B.) Am Anfang unseres Experiments wussten wir, dass das Elektron im Kasten ist – seine Wahrscheinlichkeit, drinnen zu sein, war also 1, die Wahrscheinlichkeit, nicht drinnen zu sein, war Null. Öffnen wir den Kasten, so “leckt” die Wahrscheinlichkeit (oder die Wellenfunktion) nach Draußen – je länger wir den Kasten offen lassen, um so größer ist die Wahrscheinlichkeit, das Elektron draußen zu finden.
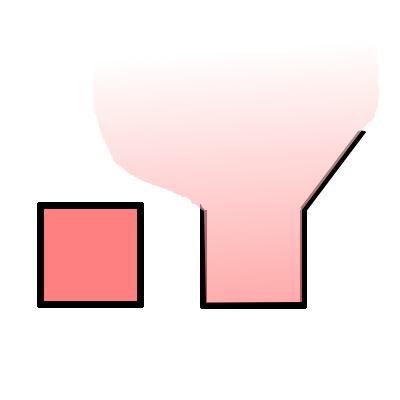
Mathematisch beschreibt man das mit der sogenannten Wellenfunktion, die gibt die Wahrscheinlichkeit an (naja, genauer gesagt ist das Quadrat der Wellenfunktion die Wahrscheinlichkeitsdichte, aber das sind mathematische Feinheiten, die für das prinzipielle Verständnis egal sind). Am Anfang ist die Wellenfunktion außerhalb des Kastens Null; wenn wir den Kasten öffnen, dann nimmt sie auch außerhalb Werte ungleich Null an. So etwa können wir das veranschaulichen (die Stärke des Rot-Tons ist ein Maß für die Wahrscheinlichkeit):
Links ist das Elektron irgendwo im Kasten, rechts ist der Kasten geöffnet, das Elektron hat jetzt auch eine Wahrscheinlichkeit, außerhalb des Kastens zu sein.
Wenn wir das Elektron dann wieder im Kasten messen, dann wissen wir jetzt, dass es wieder im Kasten ist. Dann kann es logischerweise nicht außerhalb des Kastens sein. Die Wellenfunktion ändert sich also und sieht wieder so aus wie links im Bild.
Man nennt das den “Kollaps” der Wellenfunktion – eben war sie noch an allen möglichen Orten ungleich Null, jetzt ist sie plötzlich überall Null, nur da nicht, wo wir das Elektron gemessen haben (und dort wird ihr Wert entsprechend größer).
Und wo war das Elektron, während wir es nicht gemessen haben? War es nun im Kasten, wie die ersten vier Experimente nahelegen, oder außerhalb, wie das letzte Experiment zu zeigen scheint? Darauf gibt es keine sinnvolle Antwort, das Elektron war nicht an einem bestimmten Ort, sondern über alle möglichen Orte “verschmiert”, so wie der rosafarbene Schimmer oben es zeigt.. (Dass das Elektron selbst existiert, ist aber unstrittig (oder auch nicht, siehe unten) – die Gesamtwahrscheinlichkeit, das Elektron irgendwo zu finden, ist immer gleich 1.)






Kommentare (187)