Wir können das Konzept aber retten, wenn wir unseren Atomen erlauben, sich im Raum zu bewegen. Stellt euch vor, das Kristallgitter oben im Bild würde sich entlang einer der Achsen bewegen: Dann haben wir an einem bestimmten Ort mal ein Atom und mal nicht – ganz periodisch. Die Zeitsymmetrie (das Gitter sieht zu jedem Zeitpunkt genau gleich aus) wäre gebrochen. Ist das jetzt schon ein Zeitkristall? Das wäre ziemlich banal, wann immer ich mir Zucker in den Kaffee streue, würde ich dann einen “Zeitkristall” haben, weil sich ein Kristallgitter bewegt (o.k., ich müsste meine Zuckerkörnchen genau achsparallel in den Kaffee schütten, so zwanghaft bin nicht mal ich (auch wenn ich genaue Regeln zur Auswahl der richtigen Kaffeetasse habe…)). Aber das allein reicht nicht für einen Zeitkristall, denn der soll ja seine Zeitsymmetrie spontan brechen, um seine Energie zu minimieren, und dann bitte dauerhaft in diesem Zustand bleiben. (Nach den Regeln der Quantenmechanik ist es sonst kein energetisch eindeutiger Zustand.)
Für einen Zeitkristall brauchen wir also ein System, dass sich irgendwie spontan bewegt, weil das energetisch günstig ist. Eine Idee, wie das gehen könnte, hatte zunächst Frank Wilczek, aber da sein Konzept etwas schwer zu verstehen ist, verwende ich eine Variante seines Konzepts nach Li et al., die auch den Vorteil hat, dass man sie mit aktuellen Techniken realisieren können sollte.
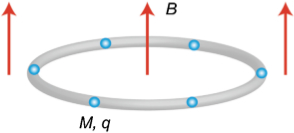
Dazu verwenden wir einzelne Ionen einer Atomsorte, die alle gleich geladen sind und sich deshalb abstoßen. Wir sperren diese Ionen mit Hilfe von passenden elektrischen Feldern so ein, dass sie die kleinst-mögliche Energie haben, wenn sie sich entlang eines Kreises anordnen:
Aus Li et al., s.u.
Da die Ionen sich gegenseitig abstoßen, werden sie auf dem Kreis einen “Kristall” bilden, bei dem sie alle brav denselben Abstand voneinander haben. Das ist ein Ringkristall, aber natürlich kein Zeitkristall, denn im Grundzustand bewegen sich die Ionen ja nicht.
Jetzt nutzen wir einen Trick aus der Quantenmechanik: Legt man ein schwaches Magnetfeld an, dann gibt es einen magnetischen Fluss durch den Ring. Die Regeln der Quantenmechanik besagen jetzt, dass ein geladenes Teilchen auf dem Ring nur dann stationär an seinem Ort verharren kann, wenn der Fluss durch den Ring ein Vielfaches des so genannten Flussquants ist. (Der Grund dafür ist ziemlich trickreich. Arg vereinfacht kann man so argumentieren: Damit ein Ion stationär auf dem Ring sitzen kann, muss seine Wellenfunktion entlang des Rings nach einem Umlauf wieder exakt denselben Wert bekommen, ohne dabei Sprünge zu haben. Legt man ein Magnetfeld an, dann beeinflusst das die Wellenfunktion, so dass das nicht mehr funktioniert. (Wer das deutlich genauer nachlesen will, kann unter den Stichworten “Aharanov-Bohm-Effekt” und “Berry-Phase” nachlesen.))
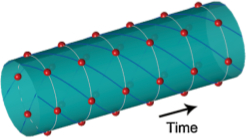
Legt man also ein schwaches Magnetfeld an, bei dem der Fluss durch den Ring kein Vielfaches des Flussquants ist, dann können die Ionen nicht mehr am Ort bleiben und müssen sich bewegen – dabei erzeugen sie ein Gegen-Magnetfeld, das dafür sorgt, dass der magnetische Fluss durch den Ring einen zulässigen Wert hat. So sieht unser Zeitkristall dann aus:
Aus Li et al., s.u.
Die Ionen laufen jetzt periodisch um den Ring herum. Aber ähnlich wie bei unserem Raumkristall ist die Sache wieder etwas komplizierter, wenn man die Quantenmechanik hinzuzieht – ohne weitere Beobachtung wird das System in einem Überlagerungszustand aus allen denkbaren umlaufenden Konfigurationen sein. Dann habe ich noch keinen Zeitkristall, weil die Wahrscheinlichkeit, ein Ion an einem bestimmten Ort zu messen, immer gleich groß ist. (So etwas kennt man übrigens schon lange von den Supraleitern, wo sich auch Ringströme um magnetische Flussschläuche bilden können.)
Damit ich einen Zeitkristall bekomme, muss ich (genau wie vorhin beim Raumkristall) eins der Ionen an einem bestimmten Ort messen, und zwar so, dass ich dabei den Zustand des Systems nicht störe. Wilczek hat sich dafür einen ziemlich komplizierten Mechanismus ausgedacht, Li et al. einen anderen, der sicherstellen soll, dass die Energie, die bei der Messung aufgewandt wird, so klein ist, dass der Zeitkristall erhalten bleibt.






Kommentare (21)