Ja, ich geb’s zu: der letzte Text über negative Temperaturen war ein bisschen theoretisch – insbesondere, weil ich kein Wort darüber gesagt habe, was die Entropie eigentlich ist. Ich wollte mal spaßeshalber versuchen zu denken wie ein echter theoretischer Thermodynamiker, also ohne jede Anschauung auf der mikroskopischen Ebene. Für ein richtiges Verständnis hilft das natürlich nur wenig, und das wurde ja auch in den Kommentaren deutlich. Heute gucken wir uns das ganze deshalb an einem Beispiel an.
Beim letzten Mal hatte ich ja erklärt, dass die Temperatur etwas mit der Änderung der Entropie zu tun hat, wenn man einem System Energie zuführt. Die Formel für die Temperatur war
Um diese Definition anschaulich zu verstehen und zu sehen, was es mit der Entropie auf sich hat, brauchen wir ein Beispielsystem. (In der Physik nennt man so etwa Spielzeugmodell oder Englisch “toy model” – dies ist ein dezenter Hinweis an den Reviewer meines letzten Papers, der das Wort “toy model” aus der Arbeit gestrichen haben wollte, weil es angeblich nicht wissenschaftlich sei (ja, manchmal springt man als Wissenschaftler durch seltsam hochgehaltene Reifen…)) Mein Lieblingsspielzeug in Sachen Thermodynamik ist das Isingmodell – das hat den Vorteil, schön einfach zu sein. (Ihr könnt das sogar online ausprobieren und damit herumspielen – das Applet hat Knöpfe zum Aufheizen und Abkühlen und viele andere schicke Möglichkeiten.)
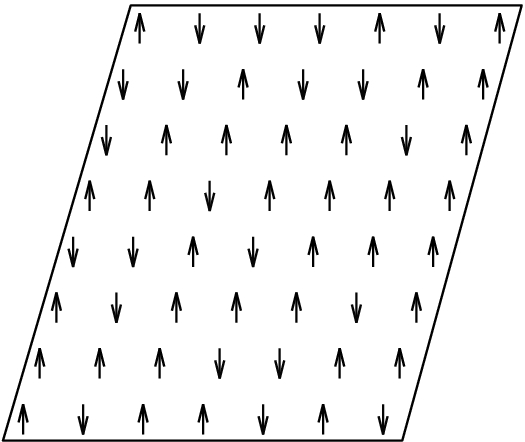
Das Ising-Modell wurde als Modell für einen Ferromagneten erfunden. In der Schule habt ihr mal gelernt, dass magnetisierbare Materialien wie Eisen kleine Elementarmagnete enthalten, die alle einen winzigen magnetischen Nord- oder Südpol haben und sich bevorzugt parallel zu einander ausrichten. Wir machen uns das Leben hier einfach und gucken uns das Modell in zwei Dimensionen an. Wir haben also ein Gitter von Elementarmagneten, die alle hübsch aufgereiht nebeneinander sitzen. Außerdem erlauben wir denen auch keine beliebige Orientierung, sondern lassen sie entweder nach oben oder nach unten zeigen; was anderes geht nicht. So etwa sieht das dann aus:
Die Energie zweier benachbarter Magneten setzen wir zu -1, wenn sie in dieselbe Richtung zeigen, und zu +1, wenn sie in entgegengesetzte Richtung zeigen (in irgendwelchen vollkommen willkürlichen Einheiten, denn hier geht es nur ums Prinzip). Übernächste Nachbarn beeinflussen sich nicht, wir müssen für die Berechnung der Energie also immer nur nächste Nachbarn angucken.
Energetisch besonders günstig ist natürlich der Zustand, wo alle Elementarmagneten in dieselbe Richtung zeigen, beispielsweise alle nach oben. Alle nach unten ist genau so gut, aber es macht die Abzählerei, die gleich kommt, etwas schwieriger (im vornehmen Physik-Sprech sagt man “der Grundzustand ist entartet” (nein, das hat nichts mit irgendwelchen Nazi-Ideen von entarteter Kunst zu tun)), deswegen betrachte ich hier nur den Fall, wo alles nach oben zeigt. (Man könnte dazu einen Elementarmagneten festhalten und in die Richtung oben zwingen, dann ist dies eindeutig der günstigste Zustand.)
Um jetzt etwas mit unserer Formel oben anfangen zu können, müssen wir die Entropie und die Energie unseres Ising-Modells kennen.
Nehmen wir an, wir haben 100 Elementarmagneten (man sagt auch gern einfach und kurz “Spins” dazu) in unserem Gitter, hübsch angeordnet auf einem Feld mit 10×10 Plätzen., die alle in dieselbe Richtung zeigen. Dann hat jeder Spin mit seinem Nachbarn eine Energie von -1, insgesamt ergibt sich -200 (wobei ich mir jetzt keine Gedanken mache, was mit den Spins am Rand passiert, Randeffekte lasse ich außen vor), denn jeder Spin hat vier Nachbarn, jede Bindung zählt mit -1, aber ich darf natürlich die Bindung zwischen zwei Nachbarn nur jeweils einmal zählen, nicht zweimal (man kann auch einfach das Gitter abklappern und von jedem Spin aus nur den Nachbarn nach rechts und nach oben angucken).
Wenn ich einen Spin umklappe, dann steigt die Energie von -200 auf -192, denn die Energie mit seinem vier Nachbarn ändert sich jeweils von -1 auf +1. Klappe ich dann noch einen zweiten Spin um, dann steigt die Energie auf -184 (es sei denn, der sitzt direkt neben dem ersten, dann ist die Energie -188, wenn ich mich nicht verzählt habe). Je mehr Spins man umklappt, um so höher wird die Energie. Dabei ist es (wie wir ja eben schon gesehen haben) etwas günstiger, wenn man viele benachbarte Spins umklappt und so “Inseln” erzeugt, weil dann im Innern der “Insel” alle Spins wieder glücklich sind, weil sie in dieselbe Richtung zeigen, und nur am Rand der Insel Energiekosten entstehen. Das führt dann zu einem ziemlich komplizierten Verhalten des Systems, bei denen man auch Inseln innerhalb von Inseln haben kann (also beispielsweise Bereiche mit Spins nach oben, in denen Bereiche mit Spin nach unten liegen, in denen Bereiche mit Spin nach oben liegen usw.). Daraus ergibt sich eine faszinierende Thermodynamik mit Phasenübergängen, kritischen Punkten und allem, was die Thermodramatiker so lieben. Hier mal ein paar Bilder des Systems bei verschiedenen Temperaturen, mit dem oben verlinkten Applet gemacht und direkt aus meinem Vorlesungsskript geklaut – die Farben symbolisieren die unterschiedlichen Spins:






Kommentare (29)