Auch Elektronen haben’s nicht leicht. Sie werden zwar nicht frustriert, weil mal wieder etwas nicht geklappt hat (“Menno. Immer muss ich im Valenzband hocken”), aber manchmal wissen sie auch nicht so recht, was sie tun sollen. Kürzlich ist es jetzt gelungen, ein System, in dem die Elektronen richtig frustriert sind, auf elegante Weise technisch herzustellen.
Aber bevor ihr jetzt denkt, ich sei völlig durchgedreht und würde neuerdings glauben, dass Elektronen leben und einen Willen haben, fahre ich mal lieber die Blog-Rhetorik etwas runter (jetzt habt ihr eh schon geklickt, muhaha) und erkläre erst mal, was es überhaupt bedeutet, wenn ein physikalisches System frustriert ist.
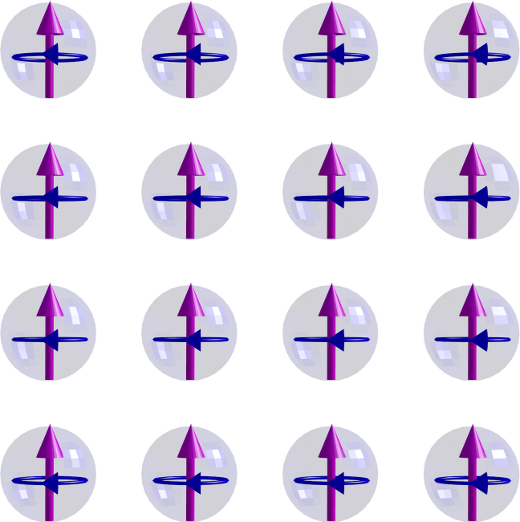
Stellt euch als erstes einen Magneten vor – in einem magnetischen Stück Materie gibt es die kleinen Elementarmagneten, die sich normalerweise parallel zueinander anordnen, das habt ihr vermutlich in der Schule gelernt. So etwa sieht das aus (praktischerweise habe ich am Wochenende gerade jede menge schicke Bilder gemacht, kann ich gleich verwenden):
Die magentafarbenen Pfeile kennzeichnen die Richtung, in die die magnetischen Momente (oder Elementarmagnete) zeigen, die kleinen blauen Schleifen drumherum sollen den Drehsinn von Elektronen kennzeichnen, die ja für den Magnetismus verantwortlich sind.
Die magnetischen Momente ordnen sich parallel an, weil das energetisch günstig ist. (Dafür ist ein komplizierter Mechanismus namens Austauschwechselwirkung verantwortlich, den keiner so ganz versteht.) Da physikalische Systeme ja dazu neigen, ihre Energie zu minimieren (warum? Guckst du hier.), tun die Momente (und damit die Elektronen) also das, was am günstigsten ist.
Es gibt aber auch Stoffe, in denen ist es energetisch günstiger, wenn sich nebeneinander liegende Momente entgegengesetzt ausrichten, das sieht dann so aus:
Hier zeigen die Momente, die nebeneinander liegen, also immer in entgegengesetzte Richtungen.
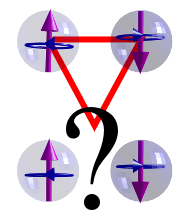
Natürlich kann man sich jetzt Systeme vorstellen, in denen beide Wechselwirkungsarten auftreten. Stellt euch vor, ihr ordnet drei Momente im Dreieck an. Moment 1 und Moment 2 haben eine niedrige Energie, wenn sie gleich ausgerichtet sind, ebenso Moment 2 und 3, aber Moment 1 und 3 möchten am liebsten entgegengesetzt ausgerichtet sein. Egal wie ihr es anstellt, eine der drei Paarungen ist immer unzufrieden und hat ein hohe Energie. Alternativ könnt ihr die drei Momente auch so wechselwirken lassen, dass jeder gern entgegengesetzt zu den beiden anderen ausgerichtet sein möchte:
Egal wie ihr’s anstellt, ihr werdet nie alle drei Momente entgegengesetzt ausrichten können. Bezeichnet man die Momente mit 1 oder 0 (für rauf und runter), dann ist klar, dass der Zustand (000) (alle drei runter) und (111) (alle drei rauf) besonders ungünstig ist. Es ist aber energetisch egal, ob ihr den Zustand (110) oder (101) oder (o11) oder (001) oder (010) oder (100) einstellt – die haben alle dieselbe Energie, und kleiner als dieser Wert kann die Energie nicht werden. Frustrierend, oder?
Und was soll daran so toll sein? Normalerweise ist es so, dass physikalische Systeme einen Grundzustand haben, in dem die Energie besonders niedrig ist. Dieser Grundzustand ist meist eindeutig (der Grundzustand der meisten Materialien ist zum Beispiel ein eingefrorener Festkörper, weil da alle Bindungskräfte am höchsten sind). Es gibt zwar Fälle, in denen auch der Grundzustand eine gewisse Freiheit hat, beispielsweise einen Magneten – im Grundzustand zeigen alle Momente in dieselbe Richtung, aber es ist egal, welche Richtung das ist. Auch hier gibt es aber nur eine globale Größe, die nicht eindeutig ist – bis auf eine bloße Rotation ist der Grundzustand immer derselbe.
In unserem frustrierten System mit den drei Spins gibt es aber gleich 6 mögliche Grundzustände. Und wenn man nicht bloß drei Spins nimmt, sondern sehr viele, und diese so miteinander koppelt, dass die Spins frustriert sind, dann gibt es extrem viele Grundzustände. Und das ist etwas, das Thermodynamikerinnen in große Aufregung versetzt – normalerweise sagt nämlich der berühmte dritte Hauptsatz der Thermodynamik, dass die Entropie eines Systems im energetisch günstigsten Zustand gleich Null ist. Und die Entropie ist nichts als ein Maß für die Zahl der Zustände (mehr darüber erfahrt ihr, wenn ihr rechts bei Artikelserien klickt, oder auch in diesem Text und seinem ersten teil hier). Frustrierte Systeme sind also solche, die die gewöhnlichen Regeln der Thermodynamik auf den Kopf stellen, weil es in ihnen sehr viele gleichwertige Grundzustände gibt. Man nennt so etwas auch ein Spin-Glas – und zumindest die Theorie der Spingläser wird schon seit langem erforscht. Spingläser sind auch nette Systeme, wenn man Optimierungsverfahren testen will (mit sowas ähnlichem habe ich mich während meiner Promotionszeit rumgeschlagen) – es ist beliebig schwierig, den energetisch günstigsten Zustand zu finden, weil es oft sehr komplexe langreichweitige Wechselwirkungen gibt.
Solche Systeme sind aber in der Realität nicht leicht zu erzeugen – normalerweise macht die Natur so etwas nicht. Es gibt zwar das sogenannte Spin-Eis, das ist aber ein ziemlich kompliziertes System und lässt sich auch nicht so leicht experimentell untersuchen (die Frustration im Spineis ist auch noch etwas komplizierter, siehe den Wiki-Artikel).
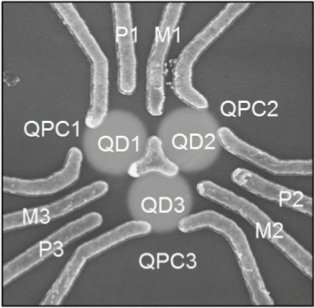
Dank der modernen Nanotechnologie ist es jetzt aber gelungen, ein vergleichsweise einfaches frustriertes System herzustellen, das drei Bestandteile hat, genau wie unser simples Bild oben. So sieht das ganze aus:
Aus Seo et al., s.u.
Was ihr hier seht ist die Oberfläche eines Halbleiters, in die einige Kontakte eingebaut wurden. Interessant für uns sind vor allem die drei eingezeichneten Bereiche, die mit QD markiert sind – das sind sogenannte Quantenpunkte (QD=quantum dot). Dicht unter der Oberfläche des Halbleiters können sich hier Elektronen in einem kleinen, nahezu perfekt zweidimensionalen Bereich tummeln. Die genauen technischen Details spare ich mir lieber (das ist Bloggerisch für “habe ich nicht verstanden”).
Entscheidend ist, dass man das System so präparieren kann, dass die drei Quantenpunkte in ähnlicher Weise miteinander wechselwirken, wie es oben unsere drei Momente getan haben. So ein Quantenpunkt kann entweder ein paar Extra-Elektronen enthalten oder auch nicht. Bezeichnen wir den Zustand, in dem die Extra-Elekronen da sind, mit 1 und den, in dem sie nicht da sind, mit 0, dann ist es auch hier wieder so, dass jeder Quantenpunkt dann die niedrigst-mögliche Energie hat, wenn seine Elektronenzahl (1 oder 0) den entgegengesetzten Wert zu den anderen beiden Punkten hat. Entsprechend gibt es auch hier wieder sechs gleich gute (oder schlechte) Zustände, genau wie eben.
Tatsächlich ist die Sache etwas komplizierter. Die Energie der Quantenpunkte hängt von den an den Kontakten angelegten Spannungen ab, die man dann variiert. Mit Hilfe der passenden Formel für die Energie des Systems kann man dann zeigen, dass sich bei richtig eingestellter Spannung an den drei Kontakten gerade die Frustration einstellt.
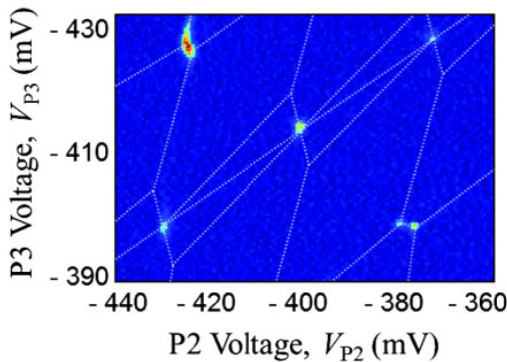
Nun muss man die Frustration natürlich auch noch nachweisen. Das geht dadurch, dass man die Leitfähigkeit misst. Stellt euch vor, wir schicken ein Elektron in den Quantenpunkt 1 und wollen von hier Strom über den Punkt 2 nach draußen leiten. Wenn wir jetzt im Zustand (100) sind, dann kostet es keine Energie, in den Zustand (110) überzugehen (die Elektronen kommen dabei aus dem Halbleitermaterial, nicht etwa aus dem Nichts), und dann in den Zustand (010), wobei wir Elektronen aus dem Punkt 2 in die entsprechende Leitung abführen. Also ist die Leitfähigkeit in diesem Zustand hoch – in anderen Zuständen (wenn man also die Spannungen so einstellt, dass man kein frustriertes System hat), ist sie dagegen niedriger.
Hier ist die Leitfähigkeit (farbig) aufgetragen gegen zwei der drei Spannungen an den Quantenpunkten, man erkennt sehr schön, dass sie bei richtig eingestellten Spannungen sehr viel größer ist (die gestrichelten Linien sind nur Hilfslinien, keine Messwerte):
Aus Seo et al., s.u.
Insgesamt ist es also gelungen, ein gut kontrollierbares frustriertes System herzustellen. Fragt sich natürlich, was man damit anfangen kann. Das ist im Moment tatsächlich noch nicht so klar – ein solches System könnte (das sagt man in solchen Fällen ja immer) beim Bau von Quantencomputern nützlich sein; wenn es gelingt, so etwas in größerem Maßstab zu bauen, könnte es auch helfen, die Thermodynamik besser zu verstehen, weil man ein gut kontrollierbares frustriertes System hätte. Ansonsten ist es erst einmal Grundlagenforschung – da weiß man vorher nie, was hinterher einer damit anfängt.
M. Seo et al., Charge Frustration in a Triangular Triple Quantum Dot
Phys. Rev. lett. 10.1103/PhysRevLett.110.046803
Gefunden via nature:
S. Andergassen, A frustrated trio, nature 495, p. 321







Kommentare (13)