Anmerkung: Es mag auf den ersten Blick verwirrend sein, dass wir die Regeln der klassischen Physik nehmen, um das Potential zu bestimmen, um dann hinterher Quantenmechanik zu betreiben – zumal in der Quantenmechanik ein Elektron, das einen ganz bestimmten Abstand zum Atomkern hat, ja gar keine eindeutige Energie besitzt. So sind aber die Spielregeln: In die Schrödingergleichung (siehe die Artikelserien) geht das Potential ein, also die Energie, die ein klassisches Elektron, das ein Punktteilchen wäre, an einem bestimmten Ort hätte. Alternativ kann man sich das vielleicht auch mit dem Pfadintegral verstehen (zu dem sage ich unten eh noch etwas): Darin betrachtet man alle denkbaren Wege, die ein Elektron als punktteilchen gehen könnte, und überlagert die dann in bestimmter Weise, um das Endergebnis auszurechnen. Also nicht verwirren lassen: Wenn ich von der Energie (oder dem Potential) an einem punkt spreche, dann ist die “klassische” Energie gemeint – ein echtes quantenmechanisches Elektron dagegen, das eine bestimmte Energie hat, sitzt nie an einem einzigen Punkt, sondern hat eine über den Raum passend verteilte Aufenthaltswahrscheinlichkeit. (Falls euch das immer noch verwirrt, dann hinterlast bitte einen Kommentar – das gilt generell für diesen Artikel, ich habe keine Ahnung, ob der für nicht Physikerinnen verständlich ist, also bitte im Zweifel unten beschweren.)
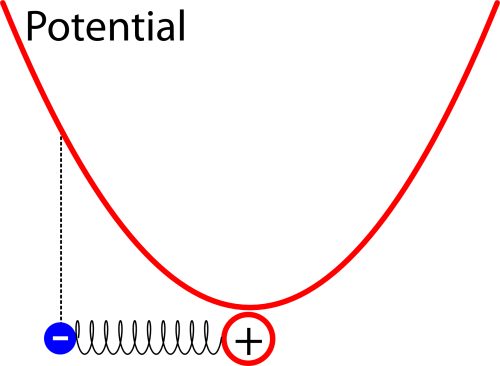
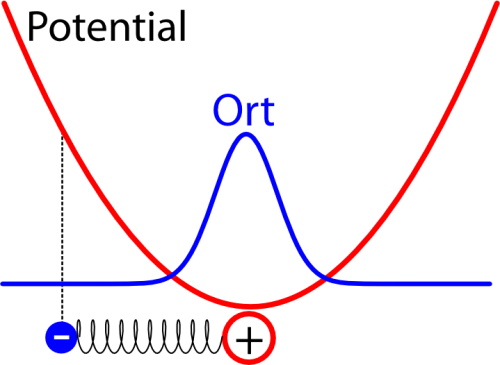
Wie der harmonische Oszillator quantenmechanisch funktioniert, habe ich neulich schon mal ausführlich erklärt, also folgt hier nur die Kurzfassung. Man kann dieses Problem relativ leicht lösen – im Zustand mit der niedrigsten Energie kommt heraus, dass das Elektron die größte Wahrscheinlichkeit dicht am Atomkern hat, aber auch in einem gewissen Abstand zum Kern gefunden werden kann. So etwa sieht die Verteilung für den Ort des Elektrons aus, wenn man sie in das Potential einzeichnet (das schematisch eingezeichnete Elektron hat dabei eigentlich keine Bedeutung mehr und soll euch nur erinnern, dass wir es mit einem Oszillator zu tun haben):
Die Breite der Verteilung hängt dabei davon ab, wie stark das Elektron an das Atom gebunden ist (also davon, wie steil die Parabel für das Potential ist) – je stärker die Bindung ist, desto schmaler ist die Verteilung und desto höher ist die Energie des Elektrons. (Dass die Energie bei stärkerer Bindung höher wird, mag verwirrend erscheinen, lässt sich aber wie folgt erklären: Wir haben den Energie-Nullpunkt ungewöhnlich gewählt, normalerweise wählt man ihn so, dass die Energie des ungebundenen Elektrons verschwindet, aber das geht hier nicht, weil die Energie mit zunehmender Entfernung immer größer wird. Man kann sich dann mit Hilfe der Unschärferelation anschaulich machen, dass ein Elektron, das auf einen schmaleren Bereich begrenzt ist und dessen Ort deswegen genauer bekannt ist, eine größere Unschärfe im Impuls haben muss, so dass die Energie größer ist.)
Also: Das Elektron hat eine Aufenthaltswahrscheinlichkeit um den Atomkern herum. Diese ist zeitlich vollkommen konstant (der Zustand hat eine eindeutige Energie und ist deswegen stationär). Messen könnt ihr diese Verteilung nur statistisch, wenn ihr sehr viele solcher Atome untersucht und den Ort des Elektrons bestimmt; dann kommt am Ende eben diese Verteilung heraus. (Ja, das ist verwirrend – aber das liegt nicht an meiner Erklärung (oder jedenfalls nicht nur) sondern einfach daran, dass die QM nun mal verwirrend ist – rechts bei den Artikelserien könnt ihr Details zu diesem Problem in den verschiedenen Artikeln nachlesen.)
Als nächstes – eigentlich geht es in diesem Artikel um die vdW-Wewi, erinnert sich noch jemand? – nehmen wir noch ein zweites identisches Atom hinzu, das wir – in einigermaßen großer Entfernung – rechts vom ersten Atom platzieren, etwa so (ich vereinfache das Bild jetzt etwas…):
Diese beiden Atome (eigentlich sollte ich wohl, weil das Modell so extrem vereinfacht ist, “Atome” in Anführungsstiche setzen, aber das spare ich mir aus Faulheit) – also diese beiden Atome wechselwirken jetzt miteinander. Um zu sehen, wie sie das tun, nehmen wir mal kurz an, die Elektronen wären jeweils an einem Ort lokalisiert und schauen auf verschiedene Möglichkeiten:







Kommentare (66)