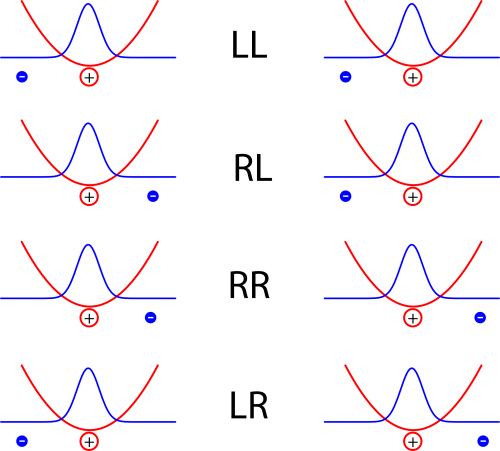
Die vier Kürzel stehen dabei für die lage der Elektronen, rechts oder links vom jeweiligen Kern
Jedes der Atome bildet hier im Bild einen Dipol, und die Energie ist natürlich dann kleiner, wenn sich positive und negative Ladungen abwechseln als wenn in der Mitte zwei positive oder zwei negative Ladungen aufeinandertreffen. Die Anordnungen LL und RR sind also energetisch günstig, LR oder RL dagegen eher ungünstig. (Warnung: Auf den ersten Blick mag das Konstrukt hier sehr an die Beschreibung des Wasserstoff-Moleküls aus diesem Artikel erinnern, wo aber ein ganz anderes Ergebnis herauskam. Der Grund ist der, dass im Modell hier die beiden Atome so weit voneinander entfernt sind, dass wir annehmen, dass es zum einen keinen Unterschied in der Energie zwischen der Anordnung LR und der Anordnung RL gibt, und dass zum anderen die Aufenthaltswahrscheinlichkeit der Elektronen in der Mitte zwischen den Atomen verschwindend klein ist.)
Falls ihr gerade verwirrt seid, dass ich erst die Elektronen mit ihrer Aufenthaltswahrscheinlichkeit beschreibe und jetzt doch wieder klassische Bildchen male: Um die Energie eines Elektrons (mit Hilfe der Schrödinger-Gleichung) zu berechnen, braucht man ja (siehe oben) das Potential, also die Energie als Funktion des Ortes für jeden Ort, die das Elektron hätte, wenn es ein klassisches Teilchen wäre – daraus kann man dann die Aufenthaltswahrscheinlichkeit berechnen.
Wir haben jetzt ein auf den ersten Blick kniffliges Problem, weil die Energien der beiden Elektronen sich gegenseitig beeinflussen. Nach den Regeln der QM passiert jetzt etwas ziemlich kompliziertes: Es gibt nicht mehr eine Aufenthaltswahrscheinlichkeit für das eine Elektron und eine zweite für das andere Elektron, sondern die beiden Wahrscheinlichkeiten sind korreliert: Die Wahrscheinlichkeit, das linke Elektron am Ort x zu finden, hängt davon ab, wo das rechte Elektron sitzt. (Mathematisch äußert sich das so, dass wir die Funktion 
Als nächstes überlegt man sich folgendes: Die Energie zwischen den beiden Atomen hängt ja davon ab, ob die Elektronen auf derselben Seite ihres jeweiligen Atoms sitzen oder nicht. Sitzen sie beide in der Mitte, also in der Anordnung RL (dann ist ihr Abstand besonders klein), ist das energetisch ungünstig, sitzen sie beiden an ihrem Atom “außen” (in der Anordnung LR), dann ist das energetisch auch schlecht. Aber wie bei Goldlöckchen und den drei Bären gibt es auch hier einen Abstand, der genau richtig ist – wenn nämlich die beiden Elektronen genau so weit voneinander entfernt sind wie die beiden Atomkerne, so wie bei den Bildern LL und RR. Deshalb ist es praktisch, wenn wir nicht die Orte der Elektronen selbst betrachten, sondern den Abstand zwischen ihnen nehmen, um das Problem zu beschreiben.
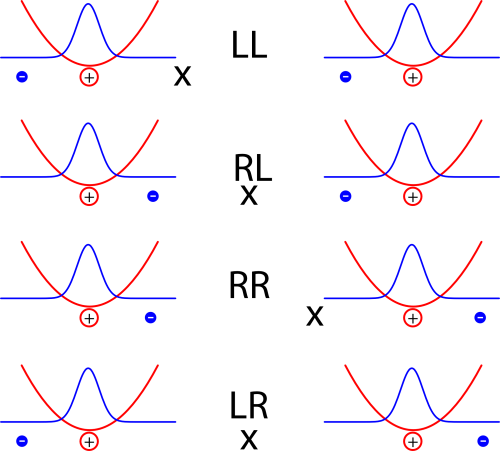
Es reicht aber natürlich nicht, den Abstand der beiden Elektronen zu kennen, um zu wissen, wo sie sind (ich brauche zwei Zahlen, für jedes Elektron eins). Zusätzlich können wir noch den Mittelpunkt (oder Schwerpunkt) zwischen den beiden Elektronen betrachten. Sitzt der genau in der Mitte zwischen den Atomen, dann ist die Anordnung der Elektronen spiegelsymmetrisch; ansonsten sind die Elektronen nach links oder rechts verschoben. Ich habe die Schwerpunkte mal mit einem x gekennzeichnet (es wurde zwar noch nie in der Geschichte der Archäologie ein Schatz bei einem “x” gefunden, aber gegen einen Schwerpunkt spricht hoffentlich nichts):
Statt das Potential also über die beiden Orte der Elektronen zu beschreiben, beschreiben wir es über den Abstand und die Lage des Schwerpunkts. Und wenn man das tut, dann zeigt sich der Nutzen unseres extrem vereinfachten Modells mit dem simplen Federgesetz: Die vorher komplizierte Gleichung zerfällt (jedenfalls für hinreichend große Atomabstände) sauber in zwei Teile. Es gibt eine Gleichung für die Lage des Schwerpunkts, eine zweite für den Abstand. Und jede dieser Gleichungen sieht genau so aus wie die Gleichung eines harmonischen Oszillators. Damit sind dann auch die Lösungen dieselben wie für den Oszillator.
Kommentare (66)