Der Schwerpunkt der beiden Elektronen ist also im Mittel so verteilt (die schwarze Kurve):
Am wahrscheinlichsten ist eine Lage in der Mitte, aber auch rechts und links von der Mitte mag sich der Schwerpunkt aufhalten.
Und der Abstand der beiden Elektronen hat diese Verteilung (das ist jetzt etwas schwierig zu zeichnen – das Bild ist so gemeint, dass ich den Nullpunkt des Abstandes immer beim linken Elektron habe; dann der Abstand zwischen den beiden Elektronen am wahrscheinlichsten, der genau dem Atomabstand entspricht. Ich hoffe, man kann das irgendwie verstehen):
Schaut man sich die Verteilungen genauer an, so stellt man fest, dass die Breite der Verteilung für die Schwerpunktslage etwas größer ist als die ursprüngliche Breite der Verteilung für eins der beiden Elektronen. Umgekehrt ist die Breite der Verteilung des Abstands etwas schmaler. Das ist auch plausibel, denn wir haben ja gesehen, dass es eben energetisch besonders günstig ist, wenn die beiden Elektronen den richtigen Goldlöckchen-Abstand haben. Umgekehrt ist es dann aber eben wahrscheinlicher, beide Elektronen links oder rechts von ihrem Atom zu finden, so dass die Breite der Verteilung für den Schwerpunkt größer ist.
In der Summe stellt sich heraus (weil die Breite der Verteilung ja etwas mit der Energie zu tun hat), dass man insgesamt durch die Wechselwirkung etwas Energie gewinnt – es ist energetisch günstiger, wenn die beiden Atome in dieser Weise wechselwirken, als wenn sie es nicht tun. Und je kleiner der Abstand der Atome ist, desto größer ist der Energiegewinn. Es ist also energetisch günstig, wenn sich die Atome annähern – mit anderen Worten: Sie ziehen sich an. Und das ist genau die vdW-WeWi.
Insofern klingt das wieder sehr ähnlich zu der Erklärung, die ich am Anfang vorgestellt habe. Aber tatsächlich ist der Zustand der Elektronen eben nicht einfach so, wie im Bild ganz oben dargestellt, so dass die Elektronen mal links und mal rechts vom Atomkern sind, sondern der Zustand ist eine Überlagerung aus solchen Bildern. Deshalb kann er auch vollkommen zeitunabhängig sein, und trotzdem ist die Wahrscheinlichkeit größer, beide Elektronen jeweils entweder rechts oder links von ihrem Atomkern zu finden.
Interessanterweise taucht diese Verwechslung zwischen dem “momentanen” (und letztlich falschen) Bild und dem tatsächlichen quantenmechanischen Bild sogar in dem zitierten Artikel auf. Dort steht: “there is a shift [of the energy] … since at any given instant of time there exists an instantaneous dipole moment in, say, atom #1. ” [Es gibt eine Verschiebung [der Energie] … weil es in jedem Moment ein momentanes Dipolmoment in beispielsweise Atom #1 gibt.] Was wieder einmal zeigt, dass auch PhysikerInnen sich gern mal etwas falsche Anschauungen basteln.
Man kann sich das ganze auch im Pfadintegral-Bild anschaulich machen (das ich ausführlich in diesem Artikel erklärt habe). Danach kann man das Verhalten von Elektronen dadurch beschreiben, dass man alle denkbaren Möglichkeiten für das, was die Elektronen tun können, aufschreibt und für jede dieser Möglichkeiten dann eine Zahl berechnet. Alle diese Zahlen aufaddiert erlauben es dann, die Wahrscheinlichkeit für einen bestimmten Prozess zu berechnen. (In dem verlinkten Artikel wird das genauer erklärt.)
Für die vdW-Wewi heißt das jetzt, dass wir zum Beispiel alle Möglichkeiten angucken können, wie zwei Elektronen, die am Anfang genau in der Mitte sitzen, das nach einem bestimmten Zeitraum wieder tun. (Der genaue mathematische Formalismus ist hier ziemlich fies, aber die Idee ist zum Glück einfach):
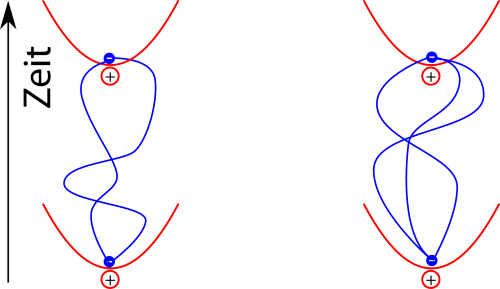
Berücksichtigt man jetzt die Wechselwirkung der elektrischen Dipole in jeder dieser Situationen, dann sieht man, dass man die beiden Elektronen nicht isoliert betrachten kann, sondern dass die Pfade sich gegenseitig beeinflussen. Pfade der Elektronen wie in diesem Bild hier
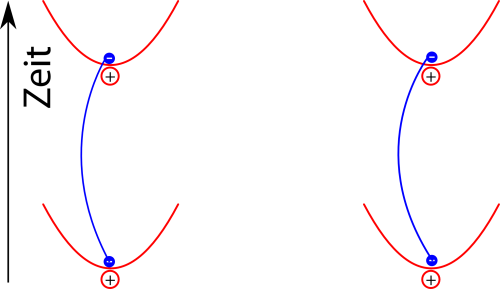
leisten dann wegen der Energieersparnis einen größeren Beitrag zum Endergebnis als zum Beispiel dieser:








Kommentare (66)