3. Andere Wellenlängen
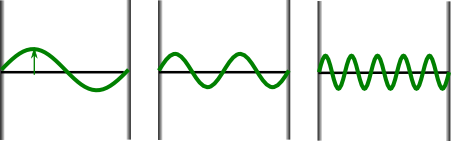
Ähnlich wie bei einer Saite, die man zum Schwingen bringt, kann man auch zwischen zwei Spiegeln Schwingungen mit “Obertönen” anregen. In der klassischen Physik sehen die Wellen dann beispielsweise so aus:
Links haben wir eine Welle, bei der die Wellenlänge gleich dem Abstand der Spiegel ist, in der Mitte eine mit Wellenlänge gleich halbem und rechts mit Wellenlänge gleich einem Fünftel Spiegelabstand. Diese Wellen oszillieren in der klassischen Physik genau so hin und her wie die Welle oben, und auch das Quantenbild dieser Wellen sieht letztlich genauso aus wie oben, also beispielsweise so (für einen Ein-Photon-Zustand):
Die Energie zu diesen Wellen ist größer als die Energie der Welle oben – da Frequenz und Wellenlänge umgekehrt proportional sind, habe ich hier wegen der kleineren Wellenlänge größere Frequenzen.
Wenn wir – damit wir nicht durcheinanderkommen, weil wir jetzt verschiedene Frequenzen haben – die Frequenz der Welle oben mit nur einem Schwingungsbauch mit ν0 bezeichnen, dann hat die Welle links (mit der halben Wellenlänge) die Energie E=2hν0. Ihr seht also, dass man eine Energie von 2hν0 auf zwei unterschiedliche Weisen bekommen kann: Entweder als Zwei-Photonen-Zustand zur Welle mit einem Schwingungsbauch, oder als Ein-Photonen-Zustand zur Welle mit zwei Schwingungsbäuchen.
Hinweis: Ja, dieser Artikel ist ziemlich lang. Ich habe überlegt, ihn in mehrere Teile zu zerhacken, habe mich aber dagegen entschlossen, damit man am Ende alles an einer Stelle zusammengefasst hat. Falls euch schon der Kopf schwirrt, macht im Zweifel ne Pause und lest später wieder weiter…
4. Überlagerungen
Wenn ihr die Überschrift dieses Abschnitts lest, denkt ihr vielleicht “Wieso Überlagerungen? Wir hatten doch schon Überlagerungen?” Aber wir können die bisherigen Zustände – so kompliziert sie auch schon waren – auch noch überlagern. Beispielsweise so:
Hier haben wir jetzt eine 70%ige Wahrscheinlichkeit, das Feld im linken Zustand vorzufinden – wenn wir beispielsweise die Energie messen, dann haben wir eine Wahrscheinlichkeit von 70% für den Wert E=hν0, und mit 30% Wahrscheinlichkeit messen wir E=4hν0.Der Zustand hier hat also keine eindeutige Energie (er ist deswegen auch nicht stationär, das gucken wir uns gleich an).
Messen wir die Amplitude und Wellenlänge (wie auch immer wir das anstellen), so bekommen wir eine Welle, die wir mit einer Wahrscheinlichkeit von x% messen, wenn wir nur den linken Zustand haben, jetzt mit einer Wahrscheinlichkeit von 0,7 x%.
Fragen wir uns dagegen, wie viele Photonen wir haben, so ist die Antwort klar: Eins. Denn wir haben einen Überlagerungszustand aus zwei Zuständen, in denen die Zahl der Photonen jeweils gleich Eins ist – wenn wir also die Photonenzahl messen (man könnte beispielsweise einen Halbleiterdetektor verwenden, denke ich (dessen Bandlücke müsste kleiner sein als hν0)), dann messen wir immer 1 Photon, nicht zwei oder 17 oder null. Insofern ist dieser Zustand hier ein Ein-Photonen-Zustand. Ob man ihn tatsächlich als “Ein Photon” bezeichnen möchte, ist schon schwieriger zu beantworten, denn wir haben ja keine klar definierte Energie mehr.
5. Wellenpakete
Wenn man sich ein Photon vorstellt, dann denkt man typischerweise an ein Teilchen, das irgendwo losfliegt und dann irgendwann woanders ankommt. Unsere photonen-Zustände hier haben diese Eigenschaft nicht – sie sind zwischen den Spiegel ausgebreitet. Irgendwie muss es aber doch möglich sein, Photonen wie einen Lichtpuls auszusenden, oder?
Ja, ist es. Dazu brauchen wir allerdings auch wieder Überlagerungszustände. (Im einzelnen habe ich den Trick, den wir hier brauchen, in der QFT-Serie erklärt.) Überlagerungen von Wellen kann man schon in der klassischen Physik bekommen. Dort können wir uns einen Lichtpuls ja etwa so vorstellen:
Wir haben ein elektrisches Feld (das Magnetfeld zeichne ich wie immer nicht mit), das nach außen verschwindet, dann ein Maximum hat und wieder abfällt. Dieses Paket bewegt sich jetzt als ganzes mit Lichtgeschwindigkeit vorwärts.








Kommentare (136)