Diese Größen – Energiedichte, Energiestrom und Spannung – lassen sich mathematisch in einem Objekt zusammenfassen, das den schicken Namen “Energie-Impus-Tensor” trägt (ich kürze das mit EIT ab). Der EIT hat nun aber die schöne Eigenschaft, dass er mathematisch genau zum Gravitonfeld “passt”; das Graviton kann als Spin-2-Teilchen genau an so ein Gebilde koppeln. (Analog wie das Photon als Spin-1-teilchen an den (vierer-)Vektor von Ladungsdichte und Strom koppelt.) In den meisten alltäglichen Situationen dominiert aber der Masse- (oder Energiedichte-)Term die Situation und man braucht sich über die anderen Komponenten keine Gedanken zu machen.
Virtuelle Gravitonen und das Newtonsche Gravitationsgesetz
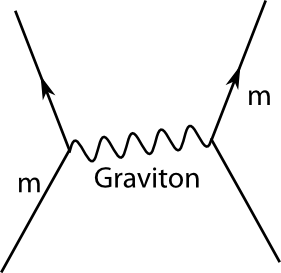
Unser Gravitonenfeld koppelt also an den EIT – insbesondere an die Masse, die in den meisten Fällen (aber nicht allen, insbesondere in der Kosmologie spielen manchmal die Spannungsterme eine wichtige Rolle) der wichtigste Term ist (die anderen Terme spielen eine ähnliche Rolle wie der Magnetismus bei der em-Wechselwirkung). Ganz analog zur QED können wir uns die Wechselwirkung zwischen zwei Massen so vorstellen, dass diese “virtuelle Gravitonen” aussenden:
So ein Feynman-Diagram sieht immer schön ordentlich aus, aber das liegt daran, dass es nur einen teil der Wahrheit beschreibt – denn die beiden Massen können ja auch zwei oder mehr Gravitonen austauschen. Jede Masse erzeugt eigentlich ständig eine Störung des Gravitonenfeldes (der Zustand ist, solange die beiden Massen am Ort bleiben, ja auch nicht von der Zeit abhängig), und eigentlich muss man alle diese Möglichkeiten überlagern. Ich habe das mal vor längerer Zeit so veranschaulicht:
Dabei sitzen die beiden Massen an den Orten x und y, die Zeitachse läuft nach oben und die “Sterne” zeigen, wie sich jeweils eine Störung von den beiden Teilchen ausbreitet.
Egal wie man die Wechselwirkung im einzelnen anguckt und berechnet – am Ende kommt heraus, dass zwischen zwei ruhenden Massen eine Kraft wirkt, die proportional zu den beiden Massen und umgekehrt proportional zum Quadrat des Abstands ist. Mit anderen Worten: das Newtonsche Gravitationsgesetz.
Unsere Quantengravitation kann also zumindest die klasssische Gravitations-Physik nach Newton herleiten. (Implizit ist hier auch angenommen, dass die Massen klein genug sind, dass ihr Gravitationsfeld selbst so wenig Energie enthält, dass wir die nicht auch noch berücksichtigen müssen. Dazu gleich mehr.)
Die Einstein-Gleichung
Aber die Einstein-Gleichung, die beschreibt, wie Raumzeitkrümmung und Materie (der EIT) zusammenhängen, sind ja wesentlich umfassender als das Newtonsche Gravitationsgesetz. Sie enthalten dieses Gesetz im Spezialfall, dass die Raumzeitkrümmung sehr schwach und der einzig wichtige Term im EIT die Masse (oder Energiedichte) ist. So sieht diese Gleichung aus:
Das fettgedruckte T auf der rechten Seite ist der EIT, den wir ja schon kennen. Davor steht ein Vorfaktor, der die Gravitationskonstante G und die Lichtgeschwindigkeit c enthält. Auf der linken Seite steht der sogenannte Einstein-Tensor – in dem steckt die Krümmung der Raumzeit drin (wie genau, drösele ich hier nicht auseinander). Wichtig am Einstein-Tensor ist, dass hier auch Terme drinstecken, in denen die Raumzeitkrümmung sozusagen auf sich selbst wirkt – eine hinreichend stark gekrümmte Raumzeit wirkt auf sich selbst zurück.
Kann unsere QG auch diese Einstein-Gleichungen herzaubern? Dass wir auf der rechten Seite den EIT stehen haben, ist ja schon mal ne feine Sache – immerhin steckt der ja auch in der Kopplung unseres Gravitonfeldes drin. Wenn man sich anschaut, wie nach unserem momentanen Stand die linke Seite der Gleichung aussehen würde, so wie wir sie aus dem, was ich bisher gesagt habe, aus der QG ableiten würde, dann sieht man, dass das noch nicht den Einstein-Tensor ergibt, sondern eine wesentlich einfachere Formel. Ist unsere QG doch fehlerhaft?
Nein, ist sie nicht. Wir haben bisher einen wichtigen Effekt vergessen: Gravitonen sind selbst ja auch Teilchen, und sie tragen auch eine Energie und einen Impuls. Das bedeutet, dass wir auch die Kopplung von Gravitonen als sich selbst berücksichtigen müssen – Gravitonen können weitere Gravitonen erzeugen. (Photonen können das nicht, weil sie ungeladen sind.) Mathematisch gesprochen macht das unsere Theorie nichtlinear, physikalisch heißt das – genau wie bei der Erklärung des Einstein-Tensors oben – dass ein Gravitonfeld selbst auch schon als Quelle für weitere Veränderungen des Gravitonfeldes dienen kann.







Kommentare (129)