Und erschwerend kommt noch hinzu, dass die Theorie eines Spin-2-Teilchens für die Gravitation zwar schick und beeindruckend ist und im Grenzfall die ART ergibt – dummerweise ist die Theorie aber nicht ganz so schick, wie man bisher denken könnte, um es vorsichtig zu sagen. Mit anderen Worten:
Die Theorie explodiert
Sieht doch alles ganz schön gut aus mit unserer Quantengravitation, oder? Wir haben uns eine Theorie eines Spin-2-Teilchens genommen und landen am Ende bei den Einsteinschen Feldgleichungen. Ziel erreicht, heiliger Gral gefunden, den nächsten Nobelpreis bitte an den Blog “Hier Wohnen Drachen” übersenden.
Tja, leider nicht. Das Dumme ist, dass uns – wenn wir sie zu Ende denken – unsere Theorie der QG schlicht um die Ohren fliegt.
Das Problem steckt in der Kopplung des Gravitons an sich selbst. Man kann es wieder mal am einfachsten mit Feynman-Diagrammen verstehen. Stellt euch ein Graviton vor, das von A nach B fliegt:
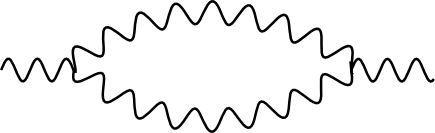
Dieses Graviton hat die Möglichkeit, sich in zwei virtuelle Gravitonen aufzuspalten, etwa so:
Das Graviton sendet also ein virtuelles Graviton aus und absorbiert es dann wieder (und da man Gravitonen nicht irgendwie beschriften kann, ist es egal, welches Graviton wir als das ursprüngliche ansehen oder ob wir sagen “aus einem Graviton werden zwei”). So etwas kennen wir auch von anderen Teilchen – wenn man solche Prozesse durchrechnet, muss man für die Teilchen, die da umlaufen, prinzipiell beliebig große Energien und Impulse erlauben, aber die dabei auftretenden Unendlichkeiten bekommt man mathematisch mit ein bisschen raffinierter Trickserei in den Griff (das ist die sogenante Renormierung, zu der habe ich hier was erklärt). Auch die hier bei unserer einfachen Gravitonen-Schleife auftretenden Unendlichkeiten lassen sich locker mathematisch in den Griff bekommen.
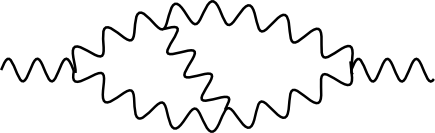
Dummerweise können aber auch die beiden virtuelle Gravitonen miteinenander noch ein Graviton austauschen, etwa so:
Tja, und hier tritt das Problem auf: Die beiden virtuellen Gravitonen können sehr hohe Energien und Impulse haben, weil sie ja virtuell sind. Unser Gravitonfeld koppelt aber ja an den EIT, also gerade an die Energie und den Impuls. Wenn die sehr groß werden, dann wird die Wahrscheinlichkeit, ein weiteres Graviton auszutauschen, ebenfalls sehr groß – und wenn man das durchrechnet, dann sieht man, dass sich die Unendlichkeiten nicht mehr wegheben lassen, egal welchen der üblichen Tricks man verwendet. (Ausführlich und etwas sauberer erklärt im Buch von Zee “QFT in a nutshell”). Und jedes weitere Graviton in dem Diagramm kann ja selbst auch ne sehr hohe Energie haben, wird also mit hoher Wahrscheinlichkeit noch weitere Gravitonen aussenden – am Ende bekommen wir einen unendlichen Wirrwarr von unendlich vielen Gravitonen, die sich vermutlich blitzartig in ein schwarzes Loch verwandeln würden. Und da wir nicht beobachten, dass jedes Teilchen mit einer Masse ständig schwarze Löcher erzeugt, stimmt da wohl was nicht mit der Theorie…
Fazit
Tja, das war’s dann wohl mit unserer schicken Spin-2-Teilchen-Theorie. Sie liefert eigentlich gute Vorhersagen (immerhin kann man die Einsteinschen Feldgleichungen ableiten) – aber wenn man sie zu Ende denkt, dann stellt man fest, dass sie eigentlich für alle Prozesse als Antwort “unendlich” vorhersagt, sobald ein Graviton von A nach B fliegen soll.
Das Problem der QG ist also nicht unbedingt, dass wir nichts darüber wissen – eigentlich muss es eine Spin-2-Teilchen-Theorie sein und diese Theorie muss eigentlich so aussehen, wie ich es hier skizziert habe. Auf der anderen Seite funktioniert so eine Theorie aber schlicht nicht. Ziel muss es also sein, eine Theorie zu finden, die einerseits die ganzen Unendlichkeiten loswird, die andererseits aber immer noch zu allem passt, was wir schon wissen. Wie man so eine Theorie finden kann, dafür gibt es unterschiedliche Ansätze – man kann es mit der Stringtheorie versuchen, oder man kann das Konzept von Raum und Zeit komplett neu aufzubauen versuchen (das macht zum Beispiel die Schleifen-QG). Bisher hat aber niemand eine Theorie gefunden, die zu all dem passt, was wir wissen, ohne dabei auch Unsinn auszuwerfen. Welche neuen Ideen man braucht, um alles unter einen Hut zu bekommen, weiß im Moment niemand.






Kommentare (129)