Da das Vor- und das Zurückschaukeln vollkommen symmetrisch sind, ist eigentlich klar, dass sich unsere mittlere Position nicht ändern kann – wir sind genau so oft vorn wie hinten, im Mittel bleiben wir also am Ort. Genauso ist es auch in unserem Kristall, so, wie wir ihn bis jetzt betrachtet haben: Die Atome schwingen zwar hin und her, aber im Mittel ist der Abstand zwischen zwei beliebigen Atomen immer noch derselbe. Von thermischer Ausdehnung also keine Spur.
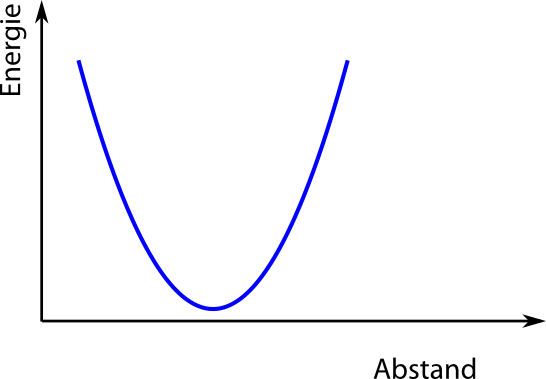
Da wir experimentell aber wissen, dass Metalle sich thermisch ausdehnen, müssen wir irgendetwas übersehen haben. Ich hab’s sogar oben schon gesagt: Der mittlere Ort ändert sich bei der Schaukel nicht, weil das Vor- und Zurückschaukeln vollkommen symmetrisch ist. Auch bei einer (idealen) Feder ist das so – auch da ist die Kraft dieselbe, wenn ich die Feder ein bisschen dehne oder sie um den selben Betrag stauche. (Ein solches Kraftgesetz nennt man auch “harmonisch” – in der Physik dient es als beliebtes Spielzeugmodell für alles mögliche, von einfachen Schwingungen bis hin zur Quantentheorie.) Wenn wir die Energie der Atome als Funktion des Abstands in diesem Modell auftragen, ergibt sich eine hübsche Parabel.
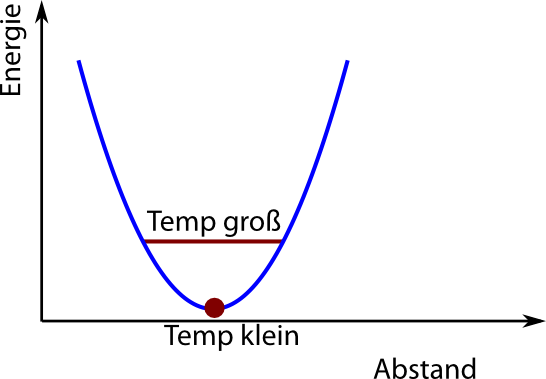
Bei niedriger Temperatur ist das System im Gleichgewicht, also ganz unten beim Zustand niedrigster Energie. Bei höherer Temperatur hat es auch eine höhere Energie, es ist deshalb mal links, mal rechts vom Gleichgewicht (ihr könnt euch vorstellen, dass es hin- und her-pendelt), aber der mittlere Abstand ändert sich nicht:
Dieses einfache Modell der Anziehung ist zwar extrem praktisch (und macht insbesondere das Berechnen vieler Dinge sehr leicht), aber es stimmt eben nicht wirklich mit der Realität überein. Die Anziehung zwischen den Eisenatomen beruht auf der Wechselwirkung ihrer Elektronen. Um die korrekt zu beschreiben, braucht man die Mittel der Quantenmechanik. Aber auch ohne ganz tief in die QM-Trickkiste zu greifen, können wir einsehen, dass die Kraft eine andere ist, wenn wir die Atome ein Stück voneinander entfernt haben als wenn wir sie einander annähern: Elektronen sind ja negativ geladen, wenn wir die Atome zu dicht zusammenquetschen, dann stoßen sich die Elektronen massiv ab. (Hinzu kommen noch quantenmechanische Effekte wie das Pauli-Prinzip.) Drücken wir die Atome extrem dicht zusammen, wird die Energie dazu extrem groß. Entfernen wir die Atome dagegen voneinander, dann nimmt die Energie nicht so schnell mit dem Abstand zu – bei sehr großer Entfernung ist die Energie auch nicht extrem groß, sonst würden sich alle Eisen-Atome im Universum ja mit gigantische Kraft anziehen.
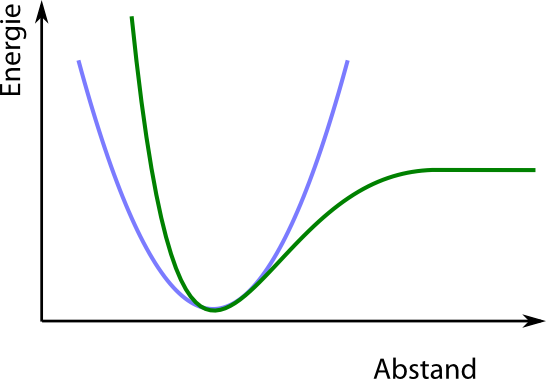
Tragen wir das wieder graphisch auf, dann sieht das Bild eher so aus (in grün die neue Energiekurve, zum Vergleich die alte symmetrische Kurve in blassblau (allerdings nicht als Frauenschrift, sondern mit inkscape generiert))
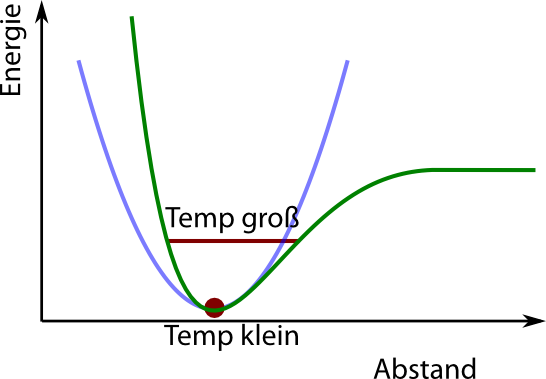
Und wenn wir jetzt den beiden Atomen etwas Energie (durch eine Temperaturerhöhung) spendieren, dann erlaubt ihnen die Extra-Energie, sich ein Stück voneinander zu entfernen, sich aber nur ein deutlich kleineres Stück aneinander anzunähern:
Wie ihr seht ist der Mittelpunkt der eingezeichneten Linie nicht mehr oberhalb der Gleichgewichtslage, sondern weiter rechts, der Abstand erhöht sich also. (Wobei ich das hier nur qualitativ angucke – quantitativ müsste man berücksichtigen, dass sich bei einer bestimmten Temperatur eine Verteilung für die Energien der Atome ergibt, so dass die Atome mal etwas höher, mal etwas tiefer sitzen. Aber das spare ich mir, es geht ja nur ums Prinzip.)
Und damit wird dann der mittlere Abstand zwischen den Atomen mit zunehmender Temperatur immer größer. Die thermische Ausdehnung kommt also daher, dass die Anziehungskraft zwischen Atomen nicht symmetrisch ist. (Vornehm ausgedrückt: Es ist ein anharmonischer Effekt, weil Schwingungen mit dem hübschen Parabel-Verlauf der Energie eben harmonisch heißen und dieser Effekt durch die Abweichung von der harmonischen Schwingung zu Stande kommt.)






Kommentare (17)