Zeitabhängigkeit
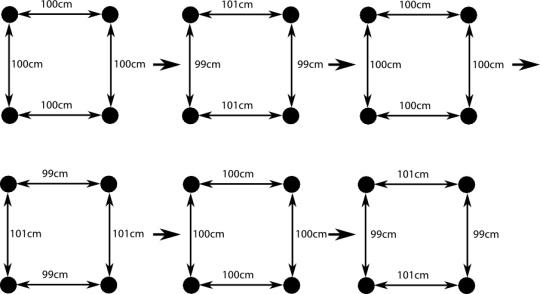
Bisher haben wir uns einen Zustand unserer Messapparatur angeschaut. Unsere Welle ist aber ja eine Welle – die Abstände zwischen den Kugeln ändern sich also mit der Zeit, und zwar so (ich zeichne jetzt nur 4 der Kugeln, sonst wird es unübersichtlich):
Vergleicht dieses Bild mit der Animation der GW oben – dann seht ihr, dass beide Darstellungen zwar unterschiedlich aussehen, aber denselben Sachverhalt beschreiben, nämlich die sich ändernden Abstände zwischen den Punkten. Nur dass diese in der einen darstellung sozusagen direkt gezeigt werden, in der anderen ändern sich dagegen nur die Zahlen an den Linien, während ich die Punkte (nicht aus Faulheit, sondern mit Absicht) nicht verschoben habe.
Zu jedem Zeitpunkt kann ich – vorausgesetzt, die Frequenz der Welle ist nicht zu hoch, so dass ich mit dem Messen nicht hinterher komme – die Abstände meiner Kugeln mit dem Maßband oder der Lichtlaufzeit messen. (Wenn die Frequenz der Welle sehr groß ist, dann muss ich berücksichtigen, dass sich die Abstände ändern, während zum Beispiel das Licht von einer Kugel zur anderen läuft. Das macht die Sache rechnerisch kompliziert, von der Idee her kommt aber nichts neues dazu.)
Unsere Kugeln sind bei der ganzen Angelegenheit vollkommen kräftefrei – jede Kugel für sich allein merkt überhaupt nichts von der GW (weil wir annehmen, dass die Kugeln sehr klein sind). Aber nehmen wir an, ich habe mein Maßband ausgerollt und habe vergessen, es wieder einzurollen, während die GW ankommt. Was passiert jetzt mit meinem Band?
Betrachten wir zwei Atome im Band. Die haben einen bestimmten Gleichgewichtsabstand, also einen Abstand, der energetisch am günstigsten ist und bei dem die Gesamtkraft auf jedes Atom Null ist, so dass alle Atome in Ruhe sind. (Naja, da gibt es noch die Nullpunktsenergie, aber die ist jetzt wirklich ne ganz andere Geschichte…) Jetzt kommt die Gravitationswelle an. So wie der Abstand zwischen den Kugeln schrumpft, schrumpft auch der Abstand zwischen den Atomen. Aber anders als die Kugeln lassen die Atome so etwas nicht mit sich machen – Atome zusammenzuschieben oder auseinanderzuzerren kostet Energie (wie ihr merkt, wenn ihr zum Beispiel ein Gummiband dehnt), die Atome “wehren sich” gegen die Verformung.
Nehmen wir an, die GW ändert den Abstand zwischen den Atomen schlagartig auf einen anderen Wert. Plötzlich sind Atome, die eben noch den Gleichgewichtsabstand hatten, zu dicht beieinander. Das lassen die sich natürlich nicht gefallen – sie streben auseinander, um wieder den Gleichgewichtsabstand zu bekommen. Weil das Ganze elastisch ist, schwingen die Atome dabei um die Gleichgewichtslage, genau wie eine Feder schwingt, wenn ihr sie auslenkt. Diese Schwingung gibt es nicht umsonst – irgendwo muss die Energie dafür ja herkommen. Also seht ihr, dass die Atome der GW Energie entziehen.
Man kann tatsächlich Gravitationswellendetektoren nach diesem Prinzip konstruieren. Dazu nimmt man einen Klotz, beispielsweise aus Stahl, und baut ihn so, dass er elastisch mit genau der Frequenz schwingt, die man detektieren möchte. Wenn die GW ankommt, bringt sie den Klotz zum schwingen, und wenn die Schwingungsfrequenz der GW zu der des Klotzes passt, wird die Schwingung immer stärker. (Das gleiche Prinzip nutzt ihr, wenn ihr ein Kind auf einer Schaukel anstoßt, auch da passt die anregende Frequenz zur Schwingfrequenz der Schaukel.) So etwas nennt man auch eine Resonanz – und wenn man es übertreibt, kommt es zur Resonanzkatastrophe. (Werdet ihr mit einer GW allerdings nie hinbekommen, dafür ist deren Energie zu schwach.) Solche Detektoren hat man übrigens schon in den 60er Jahren gebaut – allerdings ist bis auf ein paar seltsame, aber nie verlässlich bestätigte Signale dabei nie etwas herausgekommen. Nachteil eines solchen Detektors ist natürlich, dass er nur bei einer Frequenz empfindlich ist. Um GW von binären Systemen zu entdecken, die sich stabil umkreisen, wäre er also o.k., aber für das Verschmelzen von Schwarzen Löchern eignet er sich nicht.
Ist die Frequenz der GW allerdings relativ niedrig verglichen mit der Schwingfrequenz eures Objekts, dann können sich die Atome in aller Ruhe an die geänderten Abstände anpassen – die Atomabstände bleiben dann zeitlich praktisch vollkommen konstant.
Gravitationswelle und LIGO
Damit können wir jetzt auch genau nachvollziehen, was passiert, wenn eine GW auf den LIGO-Detektor trifft: Die Spiegel des Detektors hängen von äußeren Schwingungen isoliert und einigermaßen frei im Raum. Sie können sich zumindest in horizontaler Richtung praktisch kräftefrei verschieben. Die Spiegel verhalten sich also wie unsere Kugeln oben – der Abstand zwischen ihnen ändert sich im Takt mir der GW. Diese Änderung des Abstands wird durch die reflektierten Laserstrahlen gemessen.
Anders ist es mit dem Tunnel, in dem sich der Detektor befindet. Die Wände des Tunnels sind einigermaßen starr – wenn die GW auftrifft, verformen sie sich also praktisch gar nicht. Würdet ihr eine Kamera an die Tunnelwand schrauben, die den Spiegel filmt, dann würde diese Kamera aufzeichnen, wie sich der Spiegel im Tunnel vor und zurück bewegt. (Natürlich ist die Bewegung um viele Größenordnungen zu klein, als dass man da etwas sehen könnte, aber im Prinzip würde es gehen.) Würdet ihr permanent den Abstand zwischen den beiden festgeschraubten Kameras messen, so wäre dieser praktisch vollkommen konstant (von minimalen Schwingungen, die durch die GW angeregt werden, abgesehen). Die Spiegel schwingen also innerhalb des Tunnels hin und her, weil sich der Abstand zwischen ihnen ändert.
Ich hoffe, mit diesen Überlegungen ist die Sache etwas klarer.
Nachgedanken: Worin krümmt sich der Raum?
Trotz aller Bilder bleibt – wie man in den Kommentaren immer wieder merkt – bei vielen ein ungutes Gefühl zurück, weil das Ganze nicht so richtig anschaulich ist. Im Alltag haben wir es eben nie mit nennenswert messbaren Raumzeitkrümmungen zu tun (also eigentlich doch, weil die Gravitation, die wir spüren, nichts anderes ist, aber wir interpretieren die ja als Kräfte, nicht als Raumzeitkrümmung). Wie machen es denn die Abstände zwischen irgendwelchen Punkten, dass sie sich ändern? In was krümmt sich der Raum? Raum allein – liest man ja oft hier in den Kommentaren – hat doch keine Eigenschaften, wie soll er sich also krümmen können?
Zunächst mal sind das keine echten physikalischen Fragen – die Aufgabe der Physik ist es, die Natur zu beschreiben, also die besten Theorie zu finden, die zu unseren Beobachtungen passt und Vorhersagekraft hat. Wenn wir die haben – und die ART ist eine verdammt gute Theorie – dann ist das alles, was die Physik leisten kann und muss. Wir brauchen zur Beschreibung der Raumzeitkrümmungen keine Hyperräume oder so, in die wir die Raumzeit einbetten, es reicht, wenn wir Abstandswerte zwischen benachbarte Punkte im Raum (und der Zeit) schreiben. (Auf der Basis dieser Logik habe ich seinerzeit auch die Serie zur Raumzeitkrümmung geschrieben.)
Aber es kommt in meinen Augen noch etwas anderes hinzu. Nehmt mal an, die Welt würde nach den Regeln von Newton funktionieren – es gibt einen absoluten Raum, der quasi die Bühne ist, auf der sich alles abspielt. Wir packen jetzt ein Teilchen in diesen Raum. Welche Eigenschaft des Teilchens (oder des Raums) legt jetzt den Ort des Teilchens fest? Wenn der Raum ein eigenschaftsloses Gebilde ist, so wie in der Newtonschen Physik, was ändert sich dann, wenn sich ein Teilchen bewegt? Das Teilchen selbst bleibt dasselbe – es ist nur woanders. Was sich ändert, ist die Beziehung des Teilchens zum Raum, aber wenn der Raum keine Eigenschaft hat, wie kann man zu Punkten des Raumes eine Beziehung haben? (Und was sind überhaupt Punkte des Raumes?) Wenn ihr darüber eine Weile nachdenkt, dann seht ihr, dass auch diese Beschreibung ziemlich abstrakt ist. Letztlich ordnet ihr jedem Teilchen einfach drei Zahlen zu, die Koordinaten des Teilchens.
Gegenüber der Beschreibung der ART ändert sich nur, wie benachbarte Raumzeitpunkte zusammenhängen – in der klassischen Physik ist die Zeit für alle gleich, benachbarte Raumpunkte regeln ihren Abstand mathematisch über den Satz des Pythagoras. In der ART dagegen ändert sich der Zusammenhang zwischen benachbarten Raumzeitpunkten abhängig vom Ort und von der Zeit. Daran, dass Raum und Zeit letztlich ziemlich mysteriöse Konzepte sind, ändert das eigentlich nichts – es macht es für uns nur augenfälliger, weil es nicht zu unserer Alltagserfahrung passt.
PS: In den Kommentaren letztes Mal wurde ja diskutiert, es gäbe unterschiedliche “Meinungen” zur Frage, wie GW wirken. Da es sich um fundamentale Physik handelt, spielen Meinungen hier allerdings keine Rolle – hier gibt es nur richtig und falsch. Hier ein Zitat aus dem Buch “Exploring black holes” (dessen Entwurf man vor einiger Zeit kostenlos auf der Verlagsseite herunterladen konnte…), Kapitel 16. Hervorhebungen durch mich
Current gravity wave detectors on Earth are interferometers in which light
is reflected back and forth between free test masses along two perpendicular
directions, and the time difference measured between round-trip times in the
two directions. The “free” test masses are hung from wires that are in turn
supported with elaborate shock-absorbers so as to minimize the vibrations due
to passing trucks and even waves crashing on a distant shore. But the
pendulum-like motions of these test masses are free enough to permit
measurement of their change in separation due to tidal effects of a passing
gravity wave, caused by some gigantic distant event such as the coalescence of
two black holes modeled in Figure 1.
Does the change in separation induced by gravity waves affect everything,
for example a meter stick or the concrete slab on which a gravity wave
detector rests? Answer: Only by an amount that is entirely negligible. The
structure of meter sticks and concrete slabs is determined by electromagnetic
forces mediated by quantum mechanics. The two ends of a meter stick are not
freely-floating test masses. The tidal force of a passing gravity wave is much
weaker than the internal forces that maintain the shape of a meter stick—or
the concrete slab underlying the vacuum chamber and detectors of a
gravitational-wave observatory—they are stiff enough to be negligibly affected
by a passing gravity wave.






Kommentare (55)