Zunächst mal war es das 17. Jahrhundert. Die Idee, dass man die Natur mathematisch beschreiben kann, war vergleichsweise neu. Auch die Rolle von Kräften begann man gerade erst zu verstehen (Newtons Gesetze waren 1660 noch gar nicht formuliert, auch das Gravitationsgesetz kam erst später). Dass man etwas so Kompliziertes wie die Verformung von Materie mit einer so einfachen Gleichung beschreiben kann, war also schon einmal eine durchaus nicht-triviale Angelegenheit. Denn das Gesetzgalt ja nicht nur für Federn, sondern z.B. auch für die Dehnung eines Drahtes (links im Bild oben zu sehen), war also durchaus etwas Allgemeines.
Hooke selbst hat übrigens versucht, das Gesetz mit Hilfe eines einfachen Teilchenmodells herzuleiten – die Herleitung war aber fehlerhaft und hätte tatsächlich nicht zu einer Proportionalität geführt; soviel also auch zu der Behauptung, das Gesetz sei mathematisch trivial. (Ein paar Details hat der oben bereits angegebene Link. ) Nichtsdestotrotz stützte das die Idee, dass sich auch die Materie selbst möglicherweise durch mathematische Gleichungen beschreiben lässt.
Außerdem hatte Hooke auch ganz praktische Interessen – es ging ihr ja um den Uhrenbau. Und eine Feder, die eine genau dosierte Kraft ausübt, eignet sich eben hervorragend, um damit eine Uhr zu betreiben – statt als rückstellende Kraft für eine Schwingung ein Pendel zu nehmen (das zum Beispiel auf einem Schiff nicht so gut funktioniert), kann man stattdessen eine Feder verwenden. Und das Problem der genau gehenden Uhr war in der damaligen Zeit das Anwendungsproblem schlechthin, denn nur mit genauen Uhren kann man Schiffe genau navigieren.
Das Hookesche Gesetz war also zu seiner Zeit schon etwas durchaus Besonderes. Ich will aber noch auf ein paar Aspekte hinweisen, die auch heute noch genau so wichtig sind und die man mit dem Hookeschen Gesetz schön illustrieren kann.
Das eine ist eine Umkehr der Logik, die ich so ähnlich schon im Text über die Dichte erklärt habe: Wenn wir erst Mal herausgefunden haben, dass die Auslenkung einer Feder proportional zur Kraft ist, dann können wir das auch umgekehrt ausnutzen. Wir können dann nämlich eine Feder nehmen, um Kräfte zu messen, so, wie man es ja zum Beispiel mit einer Waage macht:

Von Batholith (talk) – Eigenes Werk, Gemeinfrei, https://commons.wikimedia.org/w/index.php?curid=12013054
Erst nutzen wir also Gewichte, um die Federkonstante zu bestimmen, und dann nutzen wir das, um wiederum andere Gewichte zu messen. Unter der Annahme, dass die Proportionalität hinreichend genau ist, können wir jetzt sogar Gewichte genauer bestimmen (jedenfalls relativ zu einander) als wir es vorher konnten. Wenn wir eine bestimmte Masse zum Standard erklären (so wie das Urkilogramm) und die an eine (hinreichend starke) Feder hängen, können wir die Auslenkung messen, sagen wir, sie beträgt 10cm. Wenn eine zweite Masse die Feder nur um 8cm auslenkt, dann ist diese zweite Masse eben 0.8 mal so groß wie unser Standard (also 800 Gramm, wenn wir das Urkilo nehmen). Hat ein bisschen was von Münchhausen – wir nehmen Massen, die wir möglichst genau messen, um damit herauszufinden, dass die Auslenkung der Feder proportional zur Kraft ist, dann nehmen wir das so entdeckte Prinzip, und messen damit Massen genauer, als wir es vorher konnten. Gerechtfertigt wird diese Vorgehensweise natürlich dadurch, dass sie zu sinnvollen Ergebnissen führt. (Dieses Problem der Definitionen von Größen in der Physik habe ich auch in diesem Text mal angesprochen.)
Das Hookesche Gesetz gilt übrigens nicht nur für Federn und Drähte, sondern ziemlich allgemein für Festkörper: Solange die Verformungen hinreichend klein sind (dazu gleich mehr), sind die Kraft und die Verformung des Materials zueinander proportional. Wie so oft in der Physik hat deshalb die Verallgemeinerung des Hookeschen Gesetzes für Materialien denselben Namen (Hookesches Gesetz). In der Werkstoffkunde arbeiten wir nicht direkt mit Kräften und Auslenkungen, sondern beziehen die Größen auf die Geometrie des Bauteils (Details spare ich mir). Die auf die Bauteilgröße bezogene Auslenkung ist die Dehnung (mit dem griechischen Buchstaben ε bezeichnet), die bezogene Kraft ist die Spannung σ (definiert als Kraft pro Fläche). Dann gilt in vielen Materialien die Gleichung
σ=E ε
Dabei ist E der Elastizitätsmodul, quasi das Werkstoff-Äquivalent zur Federkonstante. (Dass die Gleichung kein Minuszeichen mehr hat, liegt an der etwas anderen Definition der bezogenen Größen.) Auch die Verallgemeinerung des Hookeschen Gesetzes für Werkstoffe, die sich in unterschiedlichen Richtungen unterschiedlich verformen (wie zum Beispiel ein glasfaserverstärkter Kunststoff) heißt immer noch hookesches Gesetz, auch wenn sie mathematisch etwas komplizierter aussieht (das erkläre ich aber nicht, wenn ihr das genau wissen wollt, kann ich da ein gutes Buch empfehlen – aber wartet besser auf die 5. Auflage, die kommt im Herbst):
Das Hookesche Gesetz illustriert noch einen anderen wichtigen Aspekt von physikalischen Gleichungen, der eben schon anklang: es hat Grenzen. Das Gravitationsgesetz gilt immer – alle Massen ziehen sich an (naja, eigentlich gilt es nur näherungsweise, weil man streng genommen die Relativitätstheorie verwenden muss). Das Hookesche Gesetz aber gilt nur mit Einschränkungen: Wenn ihr eine zu große Masse an eure Feder hängt, dann dehnt sie sich irgendwann bei Erhöhung der Masse deutlich mehr als vorher, die Proportionalität geht verloren. Und wenn ihr die angehängt Masse wegnehmt, merkt ihr, dass die Feder sich nicht wieder zurückverformt – sie ist länger geworden. Ihr habt die Feder überdehnt, und dabei hat sie sich plastisch verformt.
Gleichungen in der Physik haben oft Gültigkeitsbereiche – sie gelten nicht universell, sondern nur unter bestimmten Bedingungen. (In diesem Text hier habe ich auch mal versucht, ein bisschen System in die unterschiedlichen Arten von Gleichungen in der Physik zu bringen.) Es ist ein beliebter Fehler von Leuten, die mal wieder meinen, die Physik mit ein paar Überlegungen zu revolutionieren, dass sie Gleichungen in Bereichen anwenden, wo sie nicht gelten. Auch meine Studis mache ich immer darauf aufmerksam, dass es vollkommen sinnlos ist, eine Gleichung zu lernen, wenn man nicht ihren Gültigkeitsbereich mit lernt. Wer das vergisst, dem passieren schlimme Dinge – da gab es zum Beispiel mal eine Studentin, die Werkstoffproben in die Länge gezogen hat (in einer Prüfmaschine) und dann die Bruchspannung durch die Bruchdehnung teilte uns sich wunderte, warum die Zahlenwerte nicht die waren, die man in der Literatur für die elastische Konstante des Materials findet. (Statt mal über den Anwendungsbereich der Gleichung nachzudenken, hat die Studentin dann lieber die Idee gehabt, einen Korrekturfaktor für die ja offensichtlich fehlerhafte Maschine einzuführen, stellte aber fest, dass das auch nicht funktionierte, weil der Faktor für unterschiedliche Materialien nicht übereinstimmte. Zum Glück konnte ich als Zweitprüferin noch rechtzeitig vor Abgabe der Arbeit eingreifen und das schlimmste verhindern…)
Das Hookesche Gesetz illustriert auch noch etwas anders: Physikalische Gleichungen sind dazu da, die Welt zu beschreiben, nicht, sie zu erklären. (Das habe ich schon vor langer Zeit in diesem Text ausführlich erklärt, deswegen mache ich es hier kurz.) Das merkt man in diesem Fall daran, dass das Hookesche gesetz nichts über Ursache und Wirkung aussagt. Wenn ihr eine Feder um eine bestimmte Strecke auslenkt, dann wirkt eine Kraft. Wenn ihr auf die Feder eine Kraft ausübt, dann wird sie ausgelenkt. Wie herum die Ursache-Wirkungs-Beziehung wirkt, ist in der Gleichung nicht enthalten (mathematisch gesprochen könnte man sagen, es ist eine Frage der Randbedingungen, hängt also davon ab, welche Größe ihr vorgebt). Kraft und Auslenkung sind proportional, die Kraft ist aber nicht in irgendeinem Sinne fundamentaler als die Auslenkung oder umgekehrt, das hängt immer von eurem Standpunkt (und eurer Fragestellung) ab. Die Gleichungen der Physik sollen die Zusammenhänge in der Welt beschreiben; erklären tun sie dann, wenn ihr zusätzliche Angaben macht, welche Größe ihr als Ursache und welche ihr als Wirkung ansehen wollt.
Alles in allem steckt Hookesche Gesetz also trotz seiner einfachen Form ziemlich viel Physik.

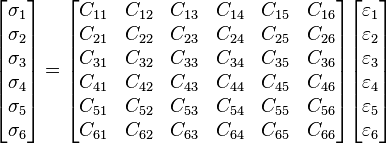





Kommentare (10)