Meeressäuger sind groß – Wale sowieso, aber auch Robben sind im Mittel größer als ihre nächsten Verwandten (wobei man sich nicht ganz sicher ist, ob das Bären oder Marderartige sind, aber so oder so, ein Walross toppt jeden Eisbären in Sachen Größe leicht). Seekühe sind auch ziemlich groß (jedenfalls größer als zum Beispiel ihre nahen Verwandten, die Klippschliefer und Erdferkel (Afrotheria), auch wenn weitere Verwandte, die Elefanten, ebenfalls nicht gerade klein sind). Lediglich Seeotter sind – für Meeressäuger – vergleichsweise klein.
Anscheinend gibt es also einen Trend, der dazu führt, dass Säugetiere, die im Meer leben, größer werden als ihre landlebenden Verwandten. Bisher wurde häufig angenommen, dass der Grund einfach der ist, dass Meeressäuger, weil sie schwimmen, es leichter haben, größer zu werden, denn landlebende Tiere haben ja mit immer größeren Problemen der Biomechanik zu kämpfen, je größer sie werden. (Etwas mehr dazu habe ich zum Beispiel hier geschrieben.) Man dachte also, dass Meeressäuger schlicht weniger eingeschränkt sind, was ihre Körpergröße angeht, und deshalb auch größer werden können.
Diese Idee wurde jetzt (Quelle siehe Ende des Artikels) detailliert getestet. Stellt sich natürlich die Frage, wie man so etwas testen soll, man kann ja nicht mal schnell ein paar Tausend Kopien der Erde anfertigen (allen Stringtheorie-Landschaftsgärtnerinnen und Multiversumsanhängerinnen zum Trotz…) und dort die Evolution der Meeressäuger statistisch auswerten. Was man aber machen kann ist, die Evolution der Säuger auf unserer Erde detailliert statistisch zu untersuchen. Wenn Meeressäuger einfach nur weniger eingeschränkt sind, was ihre Körpergröße angeht, dann sollte man erwarten, dass es insgesamt bei den Meeressäugern eine größere Varianz der Körpergröße gibt (also ein breites Spektrum an großen und kleinen Arten). Außerdem sollte man erwarten, dass es keine besondere Korrelation zwischen der mittleren Körpergröße von zum Beispiel Robben und Seekühen oder Walen gibt.
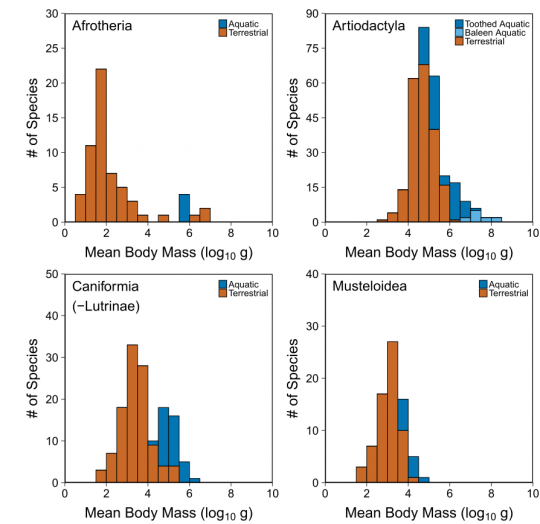
Die ausgewerteten Daten zeigen jedoch etwas anderes. Dieses Bild (aus dem Supplemental Material) zeigt das:
Aus Gearty et al., s.u.
Hier ist für die 4 Säugergruppen, zu denen auch die Meeressäuger gehören, die Körpergrößenverteilung gezeigt, in orange für die Landbewohner, in blau für die Meeressäuger. Afrotheria sind Elefanten, Seekühe, Schliefer, Erdferkel, Artiodactyla sind die “Paarhufer” (Wale sind ja mit Nilpferden verwandt), Caniformia sind die “Hundeartigen” (zu denen Marder, Hunde, Bären und eben auch Robben gehören), Musteloidea sind die Marderartigen. Aufgetragen ist jeweils die Anzahl der Arten mit einer Körpermasse in einem bestimmten Bereich, die Skala auf der x-Achse ist logarithmisch. “4” bedeutet also 10 hoch 4 Gramm= 10 Kilogramm. (Warum Biologinnen die Angewohnheit haben, auf der x-Achse bei der logarithmischen Darstellung nicht einfach die entsprechende Zahl ranzuschreiben, sondern wirklich den Logarithmus der Zahl, wird mir immer ein Rätsel bleiben, die Grafik wäre wesentlich leichter zu lesen, wenn da 1/10/100/1000 stünde…) [Und eh wieder jemand meckert, ja, auch nach der Blogpause verwende ich grammatikalisch weibliche Formen, Männer dürfen sich mitgemeint fühlen, auch wenn ich nörgle wie jetzt.]
Das Bild ist etwas schwer zu lesen, weil man nicht so recht sieht, ob sich hinter den Orange-farbigen Balken noch blaue verstecken; leider waren die Rohdaten nicht im Supplemental Material, sonst hätte ich das Bild nochmal neu gezeichnet. So oder so erkennt man aber halbwegs gut, dass das Maximum der Verteilung bei den Meeressäugern meist etwas weiter rechts liegt (sie sind also im Schnitt größer) und dass die Breite der Verteilung eher geringer ist. Etwas besser sieht man das an dieser Darstellung hier:
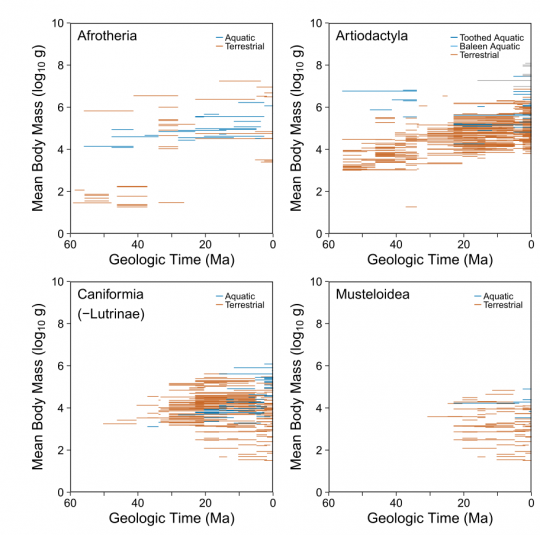
Aus Gearty et al., s.u.
Hier ist jetzt die Größe auf der y-Achse aufgetragen (wieder in doofen Logarithmen, statt direkt die Zahlen hinzuschreiben), auf der x-Achse ist die geologische Zeit dargestellt; jede Art, die man kennt, ist ein Strich. An diesem Bild sieht man sehr deutlich, dass es eigentlich keine kleinen Meeressäufer gibt und dass der evolutionäre Trend bei den landlebenden Tieren eher dahin geht, dass die Verteilung breiter wird, bei den Meeressäugern ist der Trend deutlich kleiner (was sich auch mit einer statistischen Analyse belegen lässt). Außerdem haben die Meeressäuger eine Tendenz, alle so Massen um 500 kg (auf der log-Skala also etwa bei 5,5; habe ich schon gesagt, dass ich diese Achsbeschriftung mit den Logarithmen nicht mag?) zu besitzen.
Es scheint also eher nicht so zu sein, als hätten sich die Meeressäuger von irgendwelchen biomechanischen Zwängen befreit, die Landsäugetiere in der Größe einschränken, im Gegenteil. Meeressäuger sind eigentlich immer eher groß, klein zu sein ist für sie evolutionär anscheinend ungünstig.
Fragt man sich natürlich, warum das so ist. Auch dazu gibt es eine durchaus plausible Idee. Dazu machen wir das, was Biologinnen gern tun: Wir schauen auf Skalierungsgesetze, das heißt, wie gucken, wie bestimmte Größen bei Tieren von der Körpergröße abhängen.
Egal ob Tier oder Mensch, damit ihr überleben könnt, müsst ihr genügend Nahrung zu euch nehmen. Euer Körper hat einen gewissen Grundumsatz (die Energie, die ihr verbraucht, selbst wenn ihr nur faul auf dem Sofa liegt und Serien suchtet), und wenn ihr euch gelegentlich auch mal bewegen (oder gar wachsen oder Nachwuchs bekommen wollt, was ganz klug ist, wenn eure Art nicht aussterben soll) wollt, dann müsste ihr logischerweise mehr essen als ihr per Grundumsatz verbraucht.
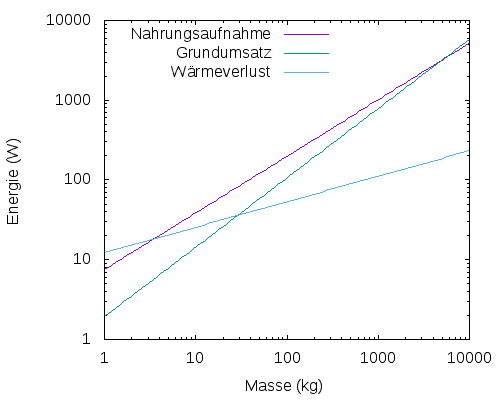
Das folgende Bild zeigt die Abhängigkeit der Energieaufnahme (Futtern) und des Grundumsatzes (Energieverbrauch beim Nichtstun) für Robben (Phocidae). Die realen Daten sind dabei gemittelt, wenn man einzelne Datenpuntke anguckt, liegen die natürlich nie alle perfekt auf der Kurve:
(Falls ihr euch wundert, warum hier vernünftige Zahlen an der Achse stehen: Das Bild habe ich selbst gemacht und nicht das aus dem paper genommen.)
Ihr seht an dem Bild, dass der Grundumsatz mit der Körpergröße etwas schneller steigt als die Nahrungsaufnahme – je größer ein Tier ist, desto schwieriger wird es also, genügend Nahrung zu finden. Das wäre also ein Grund dafür, nicht zu groß werden zu wollen. Wenn es keine weiteren Einschränkungen gibt, sollten wir also erwarten, dass Tiere alle möglichen Größen haben können, dass aber Massen im Bereich von mehr als ner Tonne eher ungünstig sind. (Man weiß ja auch, dass Elefanten sehr viel Zeit mit Fressen verbringen müssen, eben weil sie so groß sind.)
Bei den Meeressäugern scheint es aber einen weiteren Effekt zu geben, der kleine Körpergrößen ungünstig macht. Was könnte das sein? Für andere Tiere, die im Meer leben, scheint dieser Faktor nicht zu gelten; Fische sind ja auch oft klein. Meeressäuger sind aber anders als Fische gleichwarm und haben eine hohe Körpertemperatur. Wale, Robben und Seekühe schützen sich vor Kälte mit hinreichend viel Körperfett – gerade bei den Arten, die im Polarkreis rumschwimmen (oder in großen Tiefen, wo es auch kalt ist), ist das notwendig, denn die Körpertemperatur ist ja so etwa 30° größer als die Wassertemperatur. Um sich thermisch zu isolieren, braucht man also eine Fettschicht. Je dicker die ist, desto besser ist die Isolierung; kleine Meeressäuger können aber logischerweise keine 20cm dicke Fettschicht um sich rum aufbauen (sonst wären sie quasi schwimmende Fettklumpen).
Mit ein paar plausiblen Annahmen kann an den Wärmeverlust abschätzen, den ein Meeressäuger einer bestimmten Größe erleidet. Trägt man den in mein Diagramm ein, sieht das so aus:
Wenn ihr also kleiner als ein paar Kilogramm seid, dann bräuchtet ihr schon mehr Energie, um den Wärmeverlust auszugleichen, als ihr überhaupt durch Fressen aufnehmen könnt. Insgesamt darf man als Meeressäuger also nicht zu groß sein (sonst ist der Grundumsatz zu hoch) und auch nicht zu klein (sonst ist der Wärmeverlust zu hoch) – irgendwo dazwischen ist die Körpergröße “genau richtig”. (Und das erklärt auch den Titel des Blogartikels, weil Goldlöckchen ja auch alles “genau richtig” haben wollte, als sie illegal in die Wohnung der drei Bären eingedrungen ist.)
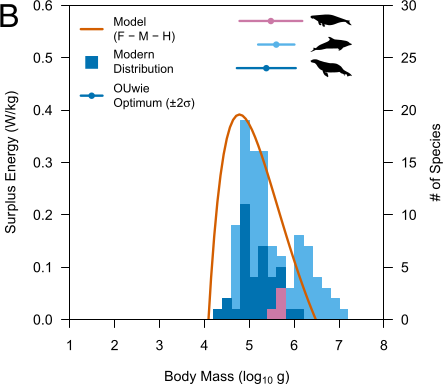
Es gibt also eine optimale Körpergröße. Um zu sehen, wo die liegt, kann man sich fragen: Bei welcher Körpermasse habe ich die meiste Überschussenergie (also aufgenommene Nahrung minus Grundumsatz minus Wärmeverlust). Diese Energie muss man natürlich auf die Körpergröße selbst normieren (klar hat ein 1000kg schweres Tier insgesamt mehr Überschussenergie als ein 50kg schweres, aber entscheidend zum Beispiel zum Wachstum ist ja, wie viel ihr bezogen auf eure Größe an Extra-Energie habt, denn das tonnenschwere Ungetüm braucht ja auch absolut mehr Energie zum Wachsen.) Das Ergebnis zeigt diese Grafik (wieder aus dem paper, deshalb auch die logarithmische Skala auf der x-Achse, die ich übrigens nicht so toll finde, hatte ich glaube ich schon erwähnt…):
Aus Gearty et al., s.u.
In orange ist die Modellvorhersage eingezeichnet, die Balken zeigen die Verteilung der Arten, oben rechts sieht man das “Optimum” aus der Artenverteilung. Die Meeressäuger haben ihr Maximum alle so im Bereich 500 Kilogramm, die rote Kurve hat ihr Maximum (das kann man in der Darstellung schlecht sehen, man hätte die x-Achse besser etwas strecken und erst bei 3 (also 1 Kilogramm, wenn man keine Logarithmen an die Achse schreiben würde…) anfangen sollen) bei etwa 56 Kilogramm. Passt also nicht optimal, aber natürlich sind diese Skalierungsdaten auch nicht in Stein gemeißelt und Schwankungen unterworfen. Es ist schade, dass es in dem paper keine Sensitivitätsstudie gibt, bei der man guckt, wie das Maximum von der genauen Skalierungsgleichung abhängt. Schiebt man die Kurve für den Grundumsatz um 50% nach oben und die für die Nahrungsaufnahme etwas nach unten, kann man zum Beispiel das Maximum zum Wert 225kg verschieben, also deutlich dichter an den gemessenen Wert.
Meeressäuger sind also anscheinend nicht von den Zwängen des Landlebens befreit, im Gegenteil: Im Wechselspiel aus Wärmeverlust und Nahrungsaufnahme bleibt ihnen gar nichts übrig, als groß zu werden.
“Energetic tradeoffs control the size distribution of aquatic mammals”







Kommentare (22)