Das Zwillingsparadoxon der Speziellen Relativitätstheorie (kurz SRT) führt ja immer gern zur Verwirrung. Das liegt nicht nur daran, dass es auf den ersten Blick unserer Intuition widerspricht, sondern vermutlich auch, dass ganz verschiedene Erklärungen des Paradoxons kursieren, die auch nicht alle wirklich zusammenpassen.
Das “Paradoxon”
Gleich vorneweg: Das Zwillingsparadoxon trägt seinen Namen nicht zu Recht – an ihm ist nichts paradox, auch wenn es auf den ersten Blick so aussehen mag. Hier nochmal in Kurzform die Idee des Paradoxons:
Die beiden Zwillingsschwestern (oder gleichaltrigen Freundinnen) Teresa und Serena müssen sich leider voneinander verabschieden: Während Teresa auf der Erde bleibt, macht sich Serena auf eine Reise nach Alpha Centauri, mehr als vier Lichtjahre von der Erde entfernt. Sie nutzt ein Hochgeschwindigkeitsraumschiff, das mit 80% der Lichtgeschwindigkeit unterwegs ist. Bei Alpha Centauri angekommen, winkt sie einmal den dort wohnenden Aliens, stellt fest, dass es ihr dort doch nicht gefällt, und macht sich auf den Rückweg zur Erde.
Bei derartig hohen Geschwindigkeiten kommt es laut SRT zum Phänomen der Zeitdilatation: Teresa sieht Serena verlangsamt, für sie sieht es so aus, als würde die Zeit für Serena langsamer laufen, so dass Serena auch langsamer altert. Da in der SRT aber Bewegungen immer nur relativ sind, sieht auch Serena Teresa verlangsamt, für sie sieht es so aus, als würde Teresa langsamer altern. Wenn Serena auf der Erde ankommt, sollte also Teresa erwarten dass sie selbst älter ist als Serena, aber umgekehrt sah Serena ja auch Teresa immer verlangsamt, sie sollte also erwarten, dass Teresa jünger ist als sie. Aber spätestens, wenn sich die beiden wieder direkt gegenüberstehen, sollte hoffentlich eindeutig zu entscheiden sein, wer nun älter ist.
Dieser scheinbare Widerspruch ist das sogenannte Zwillingsparadoxon. Um es gleich vorwegzunehmen: Die Situation ist in der Tat nicht symmetrisch, und es ist Teresa (die auf der Erde geblieben ist), die am Ende älter ist, während Serena jünger bleibt.
The Bad
Gelegentlich (beispielsweise bei dieser “Lernhelfer”-Seite – ich hab da mal ne Nachricht hinterlassen…) liest man folgende Erklärung des Zwillingsparadoxons: Um bei Alpha Centauri umzukehren, muss Serena beschleunigen. (Soweit richtig) Diese Beschleunigung benötigt eine Kraft – Serena wird in Ihren Sessel gepresst. (Auch richtig) Diese Kraft erscheint Serena wie eine Schwerkraft, sie kann beim In-den-Sessel-Gedrückt-werden nicht ohne Weiteres unterscheiden, ob sie durch ein Schwerefeld gedrückt wird oder durch die Beschleunigung, auch wenn sie natürlich weiß, dass sie gerade ihre Raketen gezündet hat. (Immer noch richtig) Weil diese Beschleunigung also äquivalent zu einer Schwerkraft ist, kann man das Zwillingsparadoxon nur dann auflösen, wenn man die SRT zu einer Theorie verallgemeinert, die auch die Schwerkraft enthält, also zur Allgemeinen Relativitätstheorie.
Nachtrag (21.2.22): Die Lernhelferseite wurde anscheinend korrigiert und jetzt wird dort korrekt über den Wechsel der Bezugssysteme argumentiert. Beschleunigungen werden allerdings immer noch erwähnt, trotzdem großes Lob.
Diese letzte Erklärung ist leider falsch. Die SRT hat überhaupt keine Probleme damit, beispielsweise die Zeitdilatation zu beschreiben, die auf eine Beobachterin wirkt, die gerade beschleunigt – das ist sogar vergleichsweise einfach. (Wer’s genau wissen will: Der Dilatationsfaktor ist zu jedem Zeitpunkt gegeben durch die momentane Geschwindigkeit, man muss also bei einer sich ändernden Geschwindigkeit lediglich aufintegrieren.) Nur Beschleunigungen, die durch die Schwerkraft zu Stande kommen, lassen sich mit der SRT nicht erfassen, alle anderen schon. (Das liegt daran, dass es laut ART eigentlich gar keine Schwerkraft gibt – wenn ihr mehr darüber wissen wollt, klickt rechts bei den Artikelserien, da gibt es sehr viele Artikel zur ART, die das erklären. Oder ihr geduldet euch bis kurz vor Weihnachten…) Ein anderes schönes Beispiel, wie die SRT Beschleunigungen korrekt berücksichtigt, findet ihr hier bzw. hier.
Dass die Erklärung mit der ART nicht funktioniert kann man übrigens auch auf eine ganz andere Weise sehen. Die SRT stammt aus dem Jahr 1905, erst 1907 hat Einstein die Logik des Äquivalenzprinzips erkannt, wonach sich eine gleichförmige Beschleunigung und ein Schwerefeld nicht unterscheiden lassen, und dann dauerte es bis 1915, bis die ART fertig war. Würde die Erklärung stimmen, dann hätten die Physikerinnen also 10 Jahre lang eine Theorie akzeptiert die in sich widersprüchliche Aussagen macht. Auch wenn manche Leute ja seltsame Ideen davon haben, wie Physikerinnen denken und glauben, dass die gesamte Physik mal eben schnell durch eine pensionierte Elektroingenieurin im Alleingang revolutioniert werden kann, die nie Physik studiert hat (ja, solche mails habe ich jede Menge in meinem Archiv) – mit der Realität hat das nicht viel zu tun. (Und falls ihr hier in den Kommentaren wieder einmal irgendwelche unsinnigen “Widerlegungen” der Relativitätstheorie posten wollt, lasst es einfach.) Eine Theorie, die derart eklatante innere Probleme mit sich bringt, hätte sicherlich niemand akzeptiert. Das Zwillingsparadoxon sollte sich innerhalb der SRT lösen lassen.
The Ugly
Kommen wir zu den Erklärungen, die zumindest richtig sind. Man kann schlicht und einfach die Gleichungen der SRT nehmen (in diesem Fall die sogenannten Lorentz-Transformationen) und die Sache einfach Schritt für Schritt nachrechnen. Die Rechnung findet ihr (mit einem kleinen Extra-Aufenthalt am Zielplaneten) ausführlich beispielsweise bei Relativitätsprinzip.info. (Dass ich diese Rechnung hier unter der Überschrift “Ugly” anführe, ist natürlich keine Kritik an Joachim Schulz, seiner Internetseite oder seinem Blog. Der weiß auch, dass man das intuitiver erklären kann, hat sich aber trotzdem netterweise die Mühe gemacht, mal alles formelmäßig auseinanderzudröseln.) Heraus kommt in der Tat, dass – in unserem Beispiel – Teresa am Ende älter ist als Serena. (Wer Zahlen mag: Bei 80% Lichtgeschwindigkeit und einer Entfernung von 4,3 Lichtjahren nach Alpha Centauri sind für Serena insgesamt nur 6,4 Jahre vergangen, für Teresa dagegen 10,8.)
Warum ich diese korrekte Herleitung mit dem Wort “ugly” belege? Weil ich das bloße Nachrechnen von Formeln immer wenig intuitiv finde – oft folgt man dem mathematischen Formalsimus, sieht am Ende ein Ergebnis, hat aber keine wirkliche Inuition gewonnen, was da eigentlich passiert.
Interessant ist an der Herleitung aber folgendes: Da ist tatsächlich von Beschleunigungen die Rede, die aber als unendlich schnell angenommen werden. Serena würde also bei Alpha Centauri ihre Geschwindigkeit sofort umkehren. (In der Rechnung ist tatsächlich noch ein Zwischenaufenthalt drin, der tut aber nix zur Sache.)
Man könnte also meinen, dass es tatsächlich die Beschleunigungen sind, die für den Unterschied der beiden Zeitabläufe verantwortlich ist. Das ist auf den ersten Blick auch sehr plausibel: Serena muss ja die Düsen ihres Raumschiffs zünden, wird dabei in ihren Sessel gedrückt etc. wie oben schon beschrieben. Aber ist das wirklich so? Dazu können wir uns ein kleines Gedankenexperiment ausdenken: Nehmen wir an, Serena wäre eine künstliche Intelligenz, ein Computerprogramm, das auf einem Supercomputer abläuft. (Und ja, ich nehme hier an, dass ein Computer ein Bewusstsein haben könnte – spielt für die Physik keine Rolle, macht die Sache aber anschaulicher.) Stellen wir uns einen zweiten, baugleichen Supercomputer vor, der sich auf einem Raumschiff befindet, das von einem entfernten Stern Richtung Erde unterwegs ist und zeitgleich mit Serena bei Alpha Centauri ankommt. Serena überträgt jetzt ihr Computerprogramm (ihr Bewusstsein) per Funk auf diesen anderen Computer. Dabei vergeht für sie keine Zeit, Zeit vergeht für sie nur auf den beiden Wegstrecken nach Alpha Centauri und zur Erde. Altert jetzt plötzlich ihr Bewusstsein anders, weil es nicht beschleunigt wurde? Nehmen wir an, Serena kopiert ihr Bewusstsein – Serena 1 wurde mit einem Funksignal übertragen, Serena 2 dagegen kehrt ihr Raumschiff zeitgleich um. Es wäre schon ziemlich seltsam, wenn für beide die Zeit vollkommen unterschiedlich vergehen würde und Serena 1 plötzlich irgendwie einen Zeitsprung macht. (Laut Wikipedia ist eine ähnliche Überlegung unter dem Namen “Drei-Brüder-Ansatz” bekannt.)
Nachtrag, in der Hoffnung, noch deutlicher zu machen, wo das Problem der Beschleunigung steckt: Nehmen wir an Serena fliegt auf dem Hinweg mit einem der Brüder mit (dem, der nach Alpha Centauri unterwegs ist), auf dem Rückweg mit dem anderen, der zur Erde fliegt. (Bruder 1 bleibt die ganze Zeit auf der Erde.) Zu jeder Zeit geht ihre Uhr gleich der Uhr des jeweiligen Bruders, bei dem sie an Bord ist. Die gesamte für sie verstrichene Zeit ist auf jedem der beiden Schiffe gleich der Zeit, die für den jeweiligen Bruder vergeht – in beiden Fällen sind es 3,2 Jahre, zusammen 6,4. Die gesamte für sie verstrichene Zeit ist also exakt gleich der Zeit, die man erhält, wenn man jeweils die Zeiten aufaddiert, die sie mit den Brüdern verbracht hat. Trotzdem sollen wir irgendwie argumentieren, dass es die Beschleunigung beim Übersetzen von einem Schiff aufs andere war, die dafür verantwortlich ist, dass für sie nicht die 10,8 Jahre von Teresa vergehen?
The Good
Entscheidend ist also anscheinend nicht die Beschleunigung, sondern etwas anderes. Das wird beispielsweise in dieser Grafik deutlich:
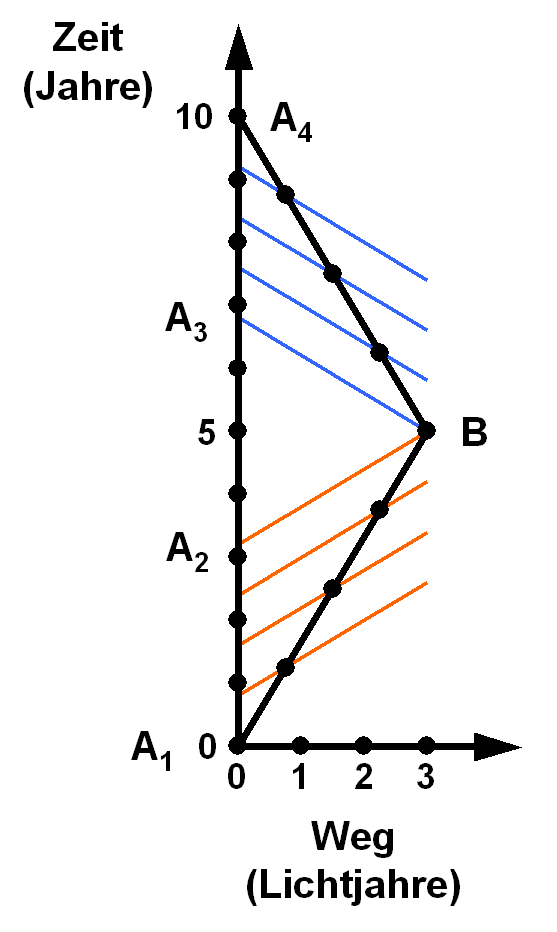
Von Wolfgangbeyer, CC BY-SA 3.0, Link
Hier seht ihr den Weg von Serena (B) bis in 3 Lichtjahre Entfernung mit einer Geschwindigkeit von 60% der Lichtgeschwindigkeit (die Zahlen sind also etwas anders als oben, weil ich zu faul war, das Bild neu zu zeichnen), eingetragen in einem Raumzeit-Diagramm. Auf der horizontalen Achse ist also der Ort (gemessen von Teresa aus) aufgetragen, auf der vertikalen Achse die Zeit, die für Teresa vergeht. Die Punkte liegen (auf der jeweiligen Achse) im Abstand von einem Jahr. Die roten und blauen Linien zeigen, welche Ereignisse für Serena jeweils zur selben Zeit stattfinden. (Sie sind also die Raumachse, die Serena verwendet.) Wenn Sie von Teresa (A) wegfliegt, dann sieht sie Teresa verlangsamt, die rote Linie, die bei Serenas zweitem Punkt (also nach zwei Jahren) liegt, trifft die senkrechte Achse, die Teresa beschreibt, an einem Punkt, wo für Teresa weniger als zwei Jahre vergangen sind. Umgekehrt zeigt eine horizontale Linie, die ihr euch bei Teresa zur Zeit nach zwei Jahren denkt, dass hier für Serena weniger als 2 Jahre vergangen sind, die Situation ist also symmetrisch. Auf dem Rückflug ist es ähnlich, auch hier könnt ihr euch leicht überzeugen, dass jede die anderen verzögert sieht (am einfachsten fangt ihr dazu oben an und guckt sozusagen in die Vergangenheit, dann ist das Bild ja genau symmetrisch).
Entscheidend ist aber – und das macht dieses Diagramm sehr schön deutlich -, dass es einen weiten Bereich von Ereignissen bei Teresa gibt, die für Serena mit gar nichts gleichzeitig sind. Und das hat nichts mit irgendwelchen Beschleunigungen zu tun, sondern nur damit, dass Serena ihr Bezugssystem wechselt. So ein Wechsel des Bezugssystems kann in der Physik oft zu scheinbaren Unstimmigkeiten in der Beschreibung führen, ein Beispiel dafür habe ich vor einiger Zeit hier erklärt. (Und hier ist die Auflösung.)
Das Zwillingsparadoxon kommt also durch einen Wechsel des Bezugssystems zustande – und da ist es egal, ob der durch Beschleunigung, Bewusstseinstransfer oder durch drei Brüder stattfindet. (Wikipedia zeigt übrigens auch noch eine Grafik, die den Fall einer kontinuierlichen Beschleunigung veranschaulicht – auch da sieht man nochmal, dass die SRT wirklich und tatsächlich kein Problem hat, mit Beschleunigungen zu hantieren.) Physikalisch ist das sicherlich eine sehr saubere und sinnvolle Erklärung, die kein bisschen in die Irre führt.
Allerdings ist “Wechsel des Bezugssystems” auf der anderen Seite auch nicht wirklich unmittelbar anschaulich. Deswegen folgt jetzt als Bonus (damit quasi besser als Clint Eastwood)
The Best
In meinem letzten Blogtext habe ich ja ein bisschen spielerisch die Idee der Raumzeit eingeführt. Wenn man diese Idee ernst nimmt, dann ist die Auflösung des Zwillingsparadoxons (zumindest für mich, andere Leute sehen das wohl anders, huhu Alderamin…) ein Kinderspiel.
Die Raumzeit können wir uns wie in dem Raumzeitdiagramm oben veranschaulichen – wir fassen sie als ein geometrisches Gebilde auf, in dem allerdings etwas seltsame Regeln für Abstände gelten. Ein Punkt in der Raumzeit (beispielsweise der Punkt A3 oben im Diagramm) kennzeichnet einen Ort und eine Zeit – sowas nennt man auch ein “Ereignis” – weil ich diesen Punkt dadurch spezifizieren kann, was genau an diesem Ort zu dieser Zeit passiert: “Um 20:19:38 berührt mein Finger die Taste ‘X’ meiner Tastatur”. Teresa folgt einer Linie in der Raumzeit, die zwei Ereignisse direkt auf geradem Weg verbindet. Serena dagegen geht nicht auf geradem Weg, sondern macht einen Umweg.
Dass ein gerader Weg eine andere Länge hat als einer der aus mehreren Stücken zusammengesetzt ist, ist uns im Raum vollkommen selbstverständlich – der gerade Weg ist die kürzeste Verbindung zwischen zwei Punkten. In der Raumzeit ist es ähnlich, nur dass hier der gerade Weg der ist, auf dem die maximale Zeit vergeht – wer einen Umweg geht, für den schlägt die Zeitdilatation (verbunden mit dem Koordinatenwechsel) zu, so dass weniger Zeit vergeht. In der Raumzeit ist der direkte Weg der, auf dem die meiste Zeit vergeht, während im Raum der direkte Weg der mit der kürzesten Strecke ist. Genau das hatte ich ja im letzten Blogartikel mit Anna Meise und Teresa Mite erklärt.
Der ominöse “Wechsel des Bezugssystems” bedeutet also schlicht, dass man zwei Abschnitte zur Messung verwendet, die entlang unterschiedlicher Richtungen liegen, und dann die gemessenen Längen einfach addiert. Wenn ich einen Kilometer nach Norden gehe, dann einen nach Osten, dann habe ich zwei Kilometer zurückgelegt, aber die Entfernung zwischen Start- und Zielpunkt beträgt eben nicht zwei Kilometer. Um Längen zu messen, muss man in einem Bezugssystem bleiben – es ist egal, wie ich mein Koordinatensystem wähle, wenn ich Achsen in Nord-Süd- und Ost-West-Richtung habe, dann muss ich die beiden Stücke entlang der Achsen nehmen und den Abstand zwischen Start und Ziel korrekt berechnen (so wie Anna Meise in meinem letzten Blogtext), oder ich wähle meine Achse gleich in Nord-Ost-Richtung, dann sehe ich sofort, dass die Entfernung zwischen Start und Ziel 1,4142…Kilometer beträgt. Was ich aber nicht tun darf ist, mein Koordinatensystem nach Lust und Laune mal hierhin und mal dorthin zeigen zu lassen und dann anzunehmen, ich könnte die so gemessenen Längen einfach addieren.
Genauso wie ich auf meinem Weg erst nach Norden und dann nach Osten tatsächlich zwei Kilometer zurückgelegt habe, genauso sind für Serena auf dem Weg nach Alpha Centauri 6,4 Jahre vergangen (bei 80% Lichtgeschwindigkeit). Aber so wie ich nicht annehmen darf, dass diese zwei Kilometer die tatsächliche Entfernung der beiden Punkte sind (weil ich ja zwischendurch die Richtung gewechselt habe), genauso darf Serena nicht annehmen, dass für Teresa auch nur diese 6,4 Jahre vergangen sind. Wer den direkten Weg im Raum geht, sieht sofort, dass ich einen Umweg gehe. Wer – wie Teresa – den direkten Weg in der Raumzeit geht, sieht ebenso leicht, dass Serena einen Umweg in der Raumzeit geht.
Das Zwillingsparadoxon ist also letztlich nur die Aussage “Ein Umweg hat eine andere Länge als direkte Weg” – und daran ist nichts paradox, sondern es ist vollkommen selbstverständlich, egal ob im Raum oder in der Raumzeit.






Kommentare (1.039)