Viele Moleküle gibt es ja in zwei Varianten, die zu einander spiegelsymmetrisch sind. Von eurer Joghurt-Packung kennt ihr vielleicht die “rechtsdrehende Milchsäure”. Die heißt nicht so, weil sie sich nur rechtsherum drehen kann, sondern wegen ihrer Wechselwirkung mit Licht. Milchsäure hat ein Kohlenstoffatom (mit einem Sternchen gekennzeichnet), das vier unterschiedliche Bindungen hat:
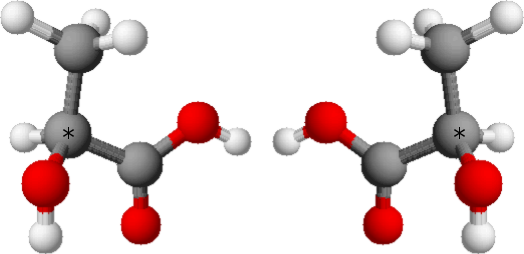
Nach einer Vorlage von Paginazero – mio disegno, Gemeinfrei, Link
Entsprechend gibt es zwei spiegelbildliche Varianten des Moleküls. Strahlt man polarisiertes Licht auf so ein Molekül, wird die Richtung der Polarisation gedreht – und zwar entweder rechtsherum oder linksherum, je nach der Molekülform. In der Natur kommen beide Formen prinzipiell vor, wobei wir aber die “rechtsdrehende” besser verdauen können als die “linksdrehende”, und das seht ihr dann auf eurer Joghurtpackung vermerkt.
So weit, so (halbwegs) einfach. Bis man anfängt, darüber nachzudenken, dass so ein Molekül aus ein paar Atomen besteht, und damit ja eigentlich nach den Regeln der Quantenmechanik beschrieben werden muss. Nach diesen Regeln ist es möglich, dass ein Objekt, dass in der klassischen Physik einen von zwei Zuständen einnehmen kann, sich in einer sogenannten “Überlagerung” aus diesen beiden Zuständen befindet. Diese “Überlagerung” gibt die Wahrscheinlichkeit an, was man misst: Man könnte also ein Milchsäure-Molekül haben, das eine 30%-Wahrscheinlichkeit für die linke Variante oben im Bild hat und eine 70%-Wahrscheinlichkeit für die rechte Variante. (Wesentlich detaillierter erkläre ich das in meiner Artikelserie “Quantenmechanik verstehen” – klickt rechts bei den Artikelserien.) Ich nenne diese beiden Varianten jetzt L und R, dann wird es einfacher.
Wir haben damit ein sogenanntes Zwei-Zustands-System (wobei wir ignorieren, dass unser Molekül noch alles mögliche andere tun könnte, beispielsweise könnten die Atome gegeneinander schwingen, Seitengruppen könnten rotieren, Elektronen könnten angeregt werden und und und…). Interessanterweise ist es so, dass die beiden Zustände oben keine eindeutige Energie besitzen.
Warum das? In der klassischen Physik ist offensichtlich die Energie des Moleküls in jedem der beiden Zustände dieselbe – die Gesetze der Physik sind ja (nahezu, von so esoterischen Dingen wie der Paritätsverletzung der elektroschwachen Wechselwirkung mal abgesehen, die ich hier nur erwähne, damit niemand nörgelt…) spiegelsymmetrisch, in unserem Alltag funktioniert eine Schraube mit Linksgewinde prinzipiell genauso gut wie eine mit Rechtsgewinde (dass wir nur die eine Sorte verwenden, ist reine Konvention).
In der Quantenmechanik gilt aber folgende Regel: Wenn wir ein System haben, das klassisch in einem von zwei Zuständen vorliegen kann, und diese beiden Zustände habe dieselbe Energie, dann gibt es einen Überlagerungszustand aus den beiden, der energetisch etwas günstiger ist, und einen zweiten Überlagerungszustand, der energetisch etwas ungünstiger ist. Der energetisch günstigste Zustand hat dabei eine Wahrscheinlichkeit von 50% L und 50% R. (Der energetisch ungünstigste übrigens auch, aber die beiden Zustände sind trotzdem nicht dieselben, weil die Überlagerung ein anderes Vorzeichen hat, das erkläre ich im Detail in besagter Artikelserie, aber nicht jetzt, sonst komme ich nämlich nie zum Thema….)
Es stellt sich nun die folgende Frage: Wenn das so ist, warum beobachten wir dann nie ein Milchsäure-Molekül in diesem energetisch günstigsten Zustand, sondern immer nur entweder in der L- oder der R-Form? Das ist das sogenannte “Hundsche Paradoxon”, das schon ganz in der Anfangszeit der Quantenmechanik (1927) aufgestellt wurde (und von dem ich peinlicherweise erst vor etwa zwei Wochen zum ersten Mal gehört habe, und ich dachte immer, ich kenne mich in der Quantenmechanik aus…).
Wenn man ein Zwei-Zustand-System zu einer bestimmten zeit in einem der beiden Zustände L oder R hat, dann ändert sich der Zustand mit der Zeit. Aus dem L-Zustand wird ein Zustand, in dem sowohl L als auch R möglich sind, dann ein reiner R-Zustand, dann wieder zurück. Das ganze ist mathematisch analog zu einem System aus gekoppelten Pendeln wie in diesem Video:
Wenn das linke Ei schwingt, entspricht das unserem Zustand L, wenn das rechte Ei schwingt, dem Zustand R, und die Schwingung überträgt sich die ganze Zeit von einem zum anderen.
Wie schnell dieser Wechsel des Zustands geht, hängt davon ab, wie groß die energetische Hürde zwischen den beiden Zuständen L und R ist – das System nutzt quasi den quantenmechanischen Tunneleffekt, um von einem zustand in den anderen zu kommen, und das Tunneln ist um so unwahrscheinlicher, je größer die Energiebarriere ist. Unser Milchsäure-Molekül müsste sich ziemlich heftig verändern, um in die Spiegelvariante zu kommen, also ist die Energiebarriere hoch. Wenn wir also einmal ein Molekül in der L-Form haben, dann müssen wir auch nach den Regeln der Quantenmechanik sehr lange (für wirklich große Werte von “sehr”) warten, bis wir eine realistische Chance haben, das Molekül im anderen Zustand vorzufinden.
Ist damit das Hundsche Paradoxon gelöst? Wir beobachten das Molekül nie in einem Überlagerungszustand, weil es solange dauert, von einem Zustand in einen anderen zu gelangen?
Nein. Denn die Frage bleibt, warum das Molekül überhaupt in den einen oder anderen der beiden Spiegelzustände kommt. Warum fängt es nicht im Überlagerungszustand an und bleibt dann dort? Hinzu kommt etwas anderes: Für große Moleküle wie die Milchsäure ist das die Tunnelzeit von L nach R und zurück lang, für kleine Moleküle gilt das aber nicht. Beispielsweise gibt es Ammoniak (das allerdings keine zwei Spiegelformen hat) in zwei Varianten, und zwischen denen kann das Molekül problemlos tunneln – damit wurde der erste Maser gebaut (ein Maser ist wie ein Laser, nur mit Mikrowellen). [Ausführlich wird diese Geschichte in den Feynman Lectures erzählt.] Es gibt auch sehr kleine Moleküle, die tatsächlich in zwei spiegelbildlichen Formen vorliegen können (solche Moleküle nennt man übrigens “chiral”, nach dem griechischein “cheir” für “Hand”).
Ein solches Molekül ist Diwasserstoff-Disulfid. Es besteht aus zwei Wasserstoff- und zwei Schwefelmolekülen. Ersetzt man den Wasserstoff durch “schweren Wasserstoff” (also Wasserstoff, bei dem im Atomkern ein Proton und ein Neutron sitzen”, dann hat man “Dideuterium-Disulfid” oder kurz D2S2, was ein bisschen wie ein Roboter aus Star Wars klingt. So sieht das Molekül aus (gelb Schwefel, blau Wasserstoff, nach Day, 2009):
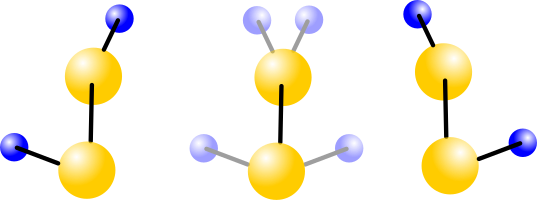
D2S2 hat eine Tunnelrate von 167 Hertz, wenn man es in einem Zustand hat, würde es also sehr schnell in den anderen tunneln, und damit spricht nichts dagegen, dass man es auch in einem Überlagerungszustand beobachten sollte. (Man nimmt genau deswegen die Variante mit Deuterium, bei der mit Wasserstoff wäre die Frequenz noch höher, das würde Rechnungen und Messungen, die man an solchen Molekülen ja auch machen kann, erschweren.) Tut man aber nicht.
Irgendetwas sorgt dafür, dass das Molekül im R- oder L-zustand beobachtet wird. Man hat lange Zeit vermutet, dass es der Einfluss der Umgebung ist, der dafür sorgt, es war aber nicht klar, wie genau das passiert. Erst im Jahr 2009 wurde die Frage durch aufwändige Computersimulation beantwortet: Verantwortlich dafür sind Stöße mit anderen Molekülen. So ein D2S2-Molekül ist ja nicht allein auf der Welt. Man kann beispielsweise simulieren, was passiert, wenn man es in eine Atmosphäre packt, die ein wenig Helium enthält. (Helium deshalb, weil es das kleinste chemisch stabile Objekt ist, das es gibt.) Die Helium-Atome und unsere D2S2-Moleküle stoßen sich dabei. Diese Stoßprozesse sind aber stark davon abhängig, welche Form das D2S2-Molekül hat: sie reagieren unterschiedlich auf die links- und die rechtshändige Form. Das mag überraschen, weil die Physik ja spiegelsymmetrisch ist, der Effekt ist aber subtil: Die Wahrscheinlichkeit für einen Stoß mit einem links- oder rechtshändigen Molekül ist tatsächlich gleich, wie man es erwarten würde. Aber in der Quantenmechanik kommt hinzu, dass die Stoßprozesse auch über eine zusätzliche Zahl beschrieben werden (die Phase), und hier gibt es einen Unterschied zwischen dem Stoß mit einem rechts- oder linkshändigen Molekül, wenn man auch noch berücksichtigt, dass die Moleküle beim Stoß mit den Helium-Atomen rotieren können. [Hinweis für die Expertinnen: In der entsprechenden Gleichung steht die Differenz der Streuamplituden, die dann quadriert wird, wie in der QM üblich. Wenn sich also die Phase der beiden Amplituden unterscheidet, hat das einen Effekt.]
Fängt man also mit lauter D2S2-Molekülen in einem Überlagerungszustand an, dann sorgen die Stöße mit den Helium-Atomen dafür, dass die Moleküle am Ende in einem von beiden möglichen Zuständen landen. Dieser Vorgang wird auch “Dekohärenz” genannt. (Nein, das quantenmechanische Messproblem ist damit nicht vollständig gelöst – denn am Ende müsste das ganze System in einem komplizierten Überlagerungszustand sein, weil jedes einzelne Molekül ja entweder im Zustand L oder R landet, der dann kompliziert mit dem verschränkt ist, was alle anderen Moleküle machen.)
Die Rechnungen zeigen auch, dass der Effekt schon bei sehr niedrigen Energien der Stoßprozesse (also bei niedrigen Temperaturen, wo die Helium-Atome langsam sind) sehr stark ist. Schon bei Temperaturen von wenig mehr als 1 Kelvin reichen etwa 10 Stoßprozesse, um ein Molekül in einen der beiden Zustände L oder R zu bringen
Damit ist das Hundsche Paradoxon also zumindest für diesen Fall geklärt, es ist der Einfluss der Umwelt, der dafür sorgt, dass wir Moleküle nicht in seltsamen Überlagerungszuständen beobachten. Theoretisch könnte man sich Vakuum-Experimente vorstellen, bei denen Überlagerungen beobachtbar wären, soweit ich weiß (falls ihr mehr wisst, sagt Bescheid), wurden die aber bisher nicht gemacht.
Quellen:
Day, Charles. “Month-long calculation resolves 82-year-old quantum paradox.” Physics Today 62.9 (2009): 16.
Trost, Johannes, and Klaus Hornberger. “Hund’s paradox and the collisional stabilization of chiral molecules.” Physical review letters 103.2 (2009): 023202.
Schachner, H. (2002). Das Hund’sche Paradoxon (Doctoral dissertation).






Kommentare (25)