Physik ist ja manchmal verwirrend und schwierig. Dass liegt nicht nur daran, dass physikalische Phänomene und Gesetze oft kompliziert sind und sich eigentlich am besten mit mathematischen Formeln beschreiben lassen. Es liegt auch daran, dass der Sprachgebrauch in der Physik oft etwas schlampig ist, und das macht dann gerade populärwissenschaftliche Erklärungen verwirrend. (Und das liegt natürlich wiederum daran, dass wir in der Physik eben meist mit Formeln hantieren, wenn wir genau sein wollen, und uns deshalb mehr Gedanken über Formelzeichen und weniger über Begriffe machen.)
Nehmen wir zum Beispiel mal den Begriff “Quant”. Der steckt ja in solchen Worten wie “Quantenmechanik” oder “Quantentheorie” drin, also den Theorien, die unsere Welt auf der fundamentalen Ebene, der der Elektronen und sonstigen Elementarteilchen, beschreiben. (Lediglich die Gravitation passt da nicht so recht rein…) Man sollte also annehmen, dass der Begriff “Quant” ein zentraler Begriff in diesen Theorien ist, deswegen heißen die ja hoffentlich so.
Das ist aber nicht wirklich so. Zwar tauchen “Quanten” in diesen Theorien durchaus auf, aber sie sind als Begriff nicht unbedingt zentral, und wenn man eine Theorie “quantisiert”, dann heißt das nicht notwendigerweise, dass jetzt alles in der Theorie mit Hilfe von “Quanten” beschrieben wird. Auch die berühmten “Quantensprünge” gibt es zwar manchmal, aber durchaus nicht immer.
Seid ihr verwirrt? Vermutlich schon. Also versuche ich heute mal, den Begriff “Quant” etwas zu entwirren und zu erklären, was ein “Quant” ist und wann und warum eine Theorie eine “Quanten”theorie ist.
Dass der Begriff ein wenig verwirrend ist, liegt an seiner Geschichte. (Das ist auch der Grund, warum ich auf meinem Blog und auch sonst selten die Entdeckungsgeschichte von etwas erkläre – meist geht der wissenschaftliche Fortschritt ja durchaus ein paar irrwege und man hantiert zwischendurch mit Begriffen und Konzepten, die sich am Ende eventuell als ungeschickt herausstellen.) Um die Verwirrung aufzudröseln, gibt es jetzt eine (stark vereinfachte, nicht quellenkritisch abgesicherte und eher cartoonartige) Geschichte, wie der Begriff “Quant” in die Welt kam und wie daraus die “Quantenmechanik” wurde, in der das “Quant” gar nicht unbedingt das zentrale Element ist. Ich sage es zur Warnung noch einmal: Diese Geschichte ist nicht in allen Details mit Quellen gestützt, ich habe einige historische Aspekte ignoriert (beispielsweise die Quantisierung des Spins) und das Ganze ist eher eine “Just-So-Story” als der Versuch, dem Begriff “Quant” sauber historisch nachzuspüren. Zu meiner Entlastung möchte ich aber dazusagen, dass das so etwa die Geschichte ist, wie man sie im Studium tatsächlich lernt (es sei denn, ihr studiert Geschichte der Physik, da ist man bestimmt genauer), und dass es ja nicht darum geht, die Geschichte selbst nachzuvollziehen, sondern darum, zu sehen, wieso der Begriff “Quant” in “Quantenmechanik” steckt, obwohl man das Wort “Quant” selbst in Büchern zur Quantenmechanik nur sporadisch findet, und wo eigentlich die Verwirrung herkommt.
Ende des 19. Jahrhunderts gab es zwar einige Leute, die glaubten, in der Physik sei schon alles erforscht, aber tatsächlich steckte die Physik voller ungelöster Probleme – die rätselhafte spezifische Wärme von Gasen, die Frage, ob die Materie nun aus Atomen besteht und wie die miteinander reagieren, das problem der Konstanz der Lichtgeschwindigkeit und noch einige mehr. (Sehr schön wird das in den Feynman Lectures On Physics erzählt.) Eins der kniffligsten Probleme war das der elektromagnetischen Strahlung, die sogenannte UV-Katastrophe. Wenn man nämlich die Gesetze der Thermodynamik und des Elektromagnetismus zusammennahm, dann konnte man vorhersagen, dass ein Material, das schwarz erscheint, Licht aussenden sollte, wenn man es erwärmt. (Die sogenannte Schwarzkörperstrahlung.) Und zwar nicht nur ein bisschen Licht, sondern unendlich viel Licht, weil die Lichtmenge bei jeder Wellenlänge letztlich immer dieselbe sein müsste, es aber ja theoretisch auch unendlich kurze Wellenlängen geben kann.
Nach der klassischen Theorie sollte ein Stück Metall, das beispielsweise eine Schmiedin in einem Feuer erhitzt, nicht rot glühen, sondern grellweiß, und es sollte gigantische Mengen UV-Strahlung abstrahlen (und auch noch Röntgenstrahlung und Gammastrahlung, die kannte man damals aber noch nicht). Da das der Erfahrung doch ein bisschen widerspricht, hatte man in der Physik ein “klitzekleines” Problem.
Dann kam Max Planck. Planck versuchte,das Problem mit ein paar simplen Modellannahmen zu lösen. Die erste war, dass die Materie, die bei Wärme strahlt, aus diskreten Objekten bestehen sollte, quasi aus Atomen. (Planck selbst glaubte zu dieser Zeit, dass die Materie kontinuierlich war, die Atome waren ein reiner “Trick”, um das Problem leichter handhabbar zu machen.) Und jedes dieser Atome würde dann Wärmeenergie aufnehmen und in Form von Strahlung wieder abgeben. Solange man dafür die ganz gewöhnlichen Gleichungen und Annahmen der klassischen Physik heranzog, änderte sich an dem ganzen Schlamassel nichts: Die Strahlung war immer noch unendlich stark. Aber was wäre – so überlegte Planck – wenn man da eine zusätzliche Regel einführt? Das Problem tritt ja bei sehr kleinen Wellenlängen (wie der UV-Strahlung) auf. Wenn es jetzt so wäre, dass es für Atome schwieriger ist Licht mit solchen kleinen Wellenlängen auszusenden, dann könnte man das Problem vielleicht lösen.
Aber was genau soll “schwieriger” bedeuten? In einem System bei einer bestimmten Temperatur ist es (ziemlich vereinfacht ausgedrückt) so, dass es sehr wahrscheinlich ist, dass Elemente des Systems kleine Energiemengen aufnehmen, und unwahrscheinlich, dass sie große Energiemengen aufnehmen. Wie wäre es also, wenn man sich vorstellt, dass man Lichtenergie nicht einfach in beliebigen Größen bekommen kann, sondern dass man Lichtenergie nur sozusagen in “Paketen” aufnehmen und wieder abgeben kann? Dann würde ein Atom nur mit einer sehr geringen Wahrscheinlichkeit genügend Energie besitzen, um UV-Licht auszusenden, aber mit einer hohen Wahrscheinlichkeit Licht mit längeren Wellenlängen.
Nebenbemerkung: Ich verfalle hier in genau die Art Darstellung, die dazu führst, dass Laien (meist pensionierte Elektrotechnik-Ingenieure [ja, die männliche Form ist in diesem Fall gezielt gemeint]) glauben, mit ein paar anschaulichen vagen Ideen die Physik revolutionieren zu können. Ansätze wie dieser von Planck sind grobe Ideen, aber selbst keine Physik. Zu Physik wird das ganze erst, wenn ihr eure Idee sauber formuliert, durchrechnet, möglichst eine Übereinstimmung mit dem Experiment bekommt und insbesondere überprüft, dass das Ganze zu dem passt, was wir schon über die Natur wissen. Solche Überlegungen erfordern detaillierte und systematische Überlegungen und vor allem Rechnungen. Die anschaulichen Startpunkte und Ideen sind genau das: Startpunkte und Ideen, aber selbst noch keine Physik. Mehr zu diesem Problem habe ich hier geschrieben. So, jetzt aber zurück zu Planck und den Quanten.
Planck nahm also diese Idee und rechnete. Heraus kam eine Formel, die perfekt zu der Menge Licht passte, die man auch experimentell von einem Schwarzen Objekt gemessen hatte. Wenn man also annahm, dass man Licht einer bestimmten Wellenlänge nicht mit beliebigen Energien erzeugen kann, sondern nur mit einem bestimmten Wert (der von der Wellenlänge abhängt), dann konnte man die Beobachtung erklären. Planck goss das ganze in eine Formel, die man so schreiben kann (Ihr dürft die Formel auch überspringen, wenn ihr gar keine Formeln mögt):
E = h c / L
Dabei ist E die Energie eines solchen “Energiepakets”, c ist die Lichtgeschwindigkeit und L die Wellenlänge. Die Größe h musste Planck einbauen, damit die Werte (und die Einheiten) zusammenpassten – später nannte man h das “Plancksche Wirkungsquantum”, was die Verwirrung noch steigern kann, wie wir gleich sehen werden. (Expertinnenhinweis: Meist schreibt man die Gleichung mit der Frequenz als E=hf, tue ich hier nicht, weil ich Wellenlängen anschaulicher finde.)
Was sagt uns diese Formel? Sie sagt uns, dass wir Lichtenergie nicht in beliebiger Größe bekommen können, sondern eben in Paketen. Nehmen wir mal rotes Licht, mit einer Wellenlänge von so etwa 750 Nanometern (0,000 000 75 Meter). Setzt man Zahlenwerte in die Formel oben ein, bekommt man eine Energie heraus, die den Wert 1.65 Elektronenvolt hat. (Das ist eine praktische Energieeinheit in der Atomphysik, abgekürzt eV – für uns ist das im Moment unwichtig, es geht nur um die Zahl.) Wenn ihr also eine rote Lampe habt, dann kann die Lichtenergie mit 1,65eV aussenden, oder mit 3,3eV (für zwei Pakete), aber nichts dazwischen. Wenn ihr stattdessen blaues Licht habt, mit einer Wellenlänge von 440 Nanometer, dann sind die Pakete etwa 2,8eV groß.
Diese “Energiepakete” nennt man auch “Quanten” oder “Lichtquanten”. (Manchmal spricht man auch von “Photonen”, aber der Begriff ist ziemlich knifflig, heute bleibe ich mal einfach bei “Quant”.) Ein Lichtquant ist also eine bestimmte Energiemenge, ein Energiepaket. Man sagt auch, dass die Energie von Licht “quantisiert” ist, weil sie eben nur in bestimmten Paketen auftreten kann.
Heißt das nun, dass es Licht generell nur in ganz bestimmten Energiemengen geben kann? Nein. Denn Licht kann ja beliebige Wellenlängen haben. Wenn ihr Lichtquanten mit einer Energie von beispielsweise 2,2 eV haben wollt, dann müsst ihr Licht mit einer Wellenlänge von 564 Nanometern nehmen, das wäre gelb. Für jede Größe der Energiepakete gibt es also eine passende Wellenlänge, bei der ihr genau dieses Paket bekommt.
Die Lichtenergie ist also quantisiert in dem Sinne, dass ihr Lichtenergie immer nur in Paketen erzeugen oder verschlucken könnt, deren Größe von der Wellenlänge abhängt. Wenn euch die Wellenlänge aber egal ist, dann könnt ihr Quanten mit jedem beliebigen Wert der Energie erzeugen. Es ist also nicht so, als gäbe es da “Lücken” in den Energiewerten und als gäbe es zu bestimmten Energien einfach gar keine passenden Lichtquanten. Wie wir gleich sehen werden, ist das bei “quantisierten Energieniveaus” wie im Wasserstoffatom anders.
Eine weitere Quelle der Verwirrung ist die Konstante h, das “Plancksche Wirkungsquantum” aus der Formel oben. Diese Konstante sorgt für die Umrechnung von Wellenlänge in Energie. Sie hat die physikalische Einheit Joule mal Sekunde. Weil alles, was diese Einheit hat, in der Physik auch als “Wirkung” bezeichnet wird, steckt der Begriff “Wirkung” auch im namen der Konstante. Verwechselt das aber nicht mit dem Alltagsbegriff – es muss nicht etwas “wirken”, nur weil irgendwo eine Größe im Spiel ist, die die Einheit einer “Wirkung” hat.
Schlimmer am Namen “Plancksches Wirkungsquantum” ist aber, dass er suggeriert, diese Größe selbst ist irgendwie ein “Quant”, also eine Menge von irgendwas. Ist sie nicht, sie ist ein Umrechnungsfaktor, um die Größe eines Lichtquants aus der Wellenlänge auszurechnen. Ein besserer Name wäre also zum Beispiel “Plancksche Quantenkonstante” gewesen, dann wäre klarer, dass die Größe selbst kein Quant ist. Der Name suggeriert, dass die Größe h sozusagen eine Einheit ist, und dass Quanten dann vielleicht in Paketen der Größe 1h, 2h, 3h usw. vorkommen, aber so ist es nicht. (Expertinnenhinweis: Beim Drehimpuls ist es tatsächlich so, dass man halbzahlige Vielfache von h-quer hat, ich weiß. Deswegen ist der Begriff “Wirkungsquantum” zumindest in dem Zusammenhang etwas sinnvoller. Aber wer das weiß, der ist hoffentlich vom Begriff “Quant” auch nicht mehr verwirrt…)
Soweit Planck. Einstein hat dann auch noch etwas beigetragen und hat (mit der Erklärung des sogenannten “Photoeffekts”) gezeigt, dass diese Lichtquanten nicht bloß eine hypothetische Rechnegröße sind, sondern physikalisch beobachtbare Effekte vorhersagen – Licht wird tatsächlich in Paketen mit dieser Größe absorbiert und emittiert.
Als nächstes springen wir so ins Jahr 1913. Da hat sich Niels Bohr mit Atomen und Atomspektren beschäftigt und hat das berühmte “Bohrsche Atommodell” aufgestellt. Danach kann man sich ein Atom so vorstellen, dass die Elektronen sich auf Kreisbahnen bewegen, und zwar nicht auf beliebigen Kreisbahnen, sondern nur auf ganz bestimmten.Wenn die Elektronen sich von einer Bahn auf eine andere bewegen, dann tun sie das “sprunghaft” und senden dabei ein Lichtquant aus oder absorbieren es, je nachdem, wie die Energien sich verhalten. Das Bild hier zeigt beispielsweise ein Elektron, das von der dritten zur zweiten Bahn springt und dabei ein Lichtquant mit Energie ΔE=h ν aussendet (das ist unsere Formel von oben, nur mit der Frequenz statt der Wellenlänge geschrieben):
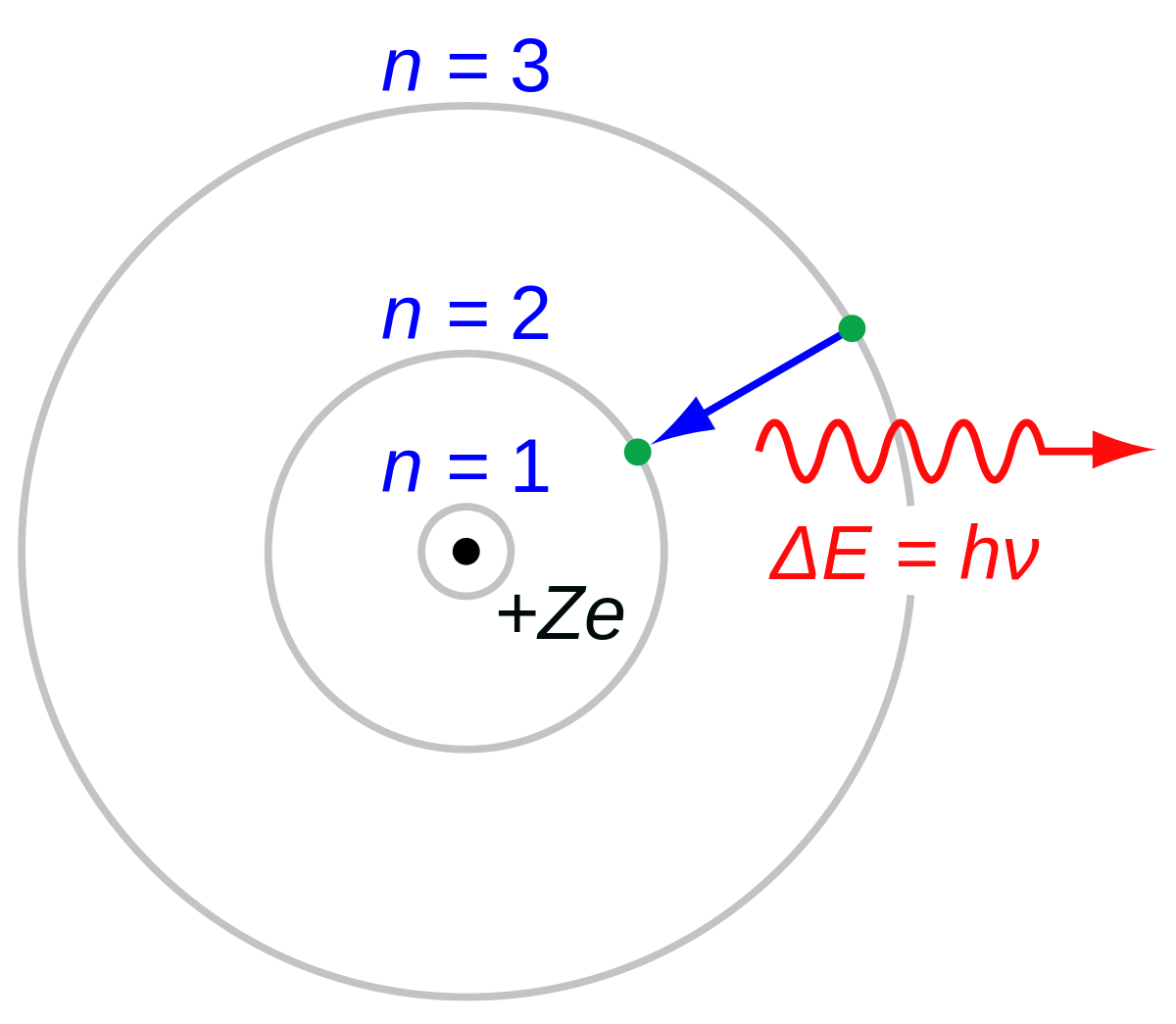
Von JabberWok, CC BY-SA 3.0, Link
Es sind also nicht beliebige Bahnen für die Elektronen möglich – anders als zum Beispiel bei den Bahnen von Planeten um die Sonne, die natürlich beliebige Abstände haben können. Vielmehr sind die Bahnen diskret, mit “Lücken” dazwischen. Zu jeder Bahn gehört auch ein Wert der Energie (immer negativ, weil die Elektronen ja gebunden sind), und auch diese Energien sind diskret. Das Elektron im Grundzustand des Wasserstoffatoms (n=1 oben im Bild) hat zum Beispiel eine Energie von -13,6eV, auf der nächst-höheren Bahn ist die Energie dann -3,4eV und so weiter. Die Energie kam also auch hier nur in bestimmten Größen und konnte nicht beliebige Werte annehmen, also war sie auch “quantisiert” oder “gequantelt”. Hier ist es jetzt tatsächlich so, dass es zu bestimmten Energiewerten keinen möglichen Zustand gibt – es gibt keine Möglichkeit, ein Elektron im Wasserstoffatom mit einer Energie von -10eV zu haben. (Expertinnenhinweis: Ihr könnt natürlich durch Linearkombination einen Erwartungswert von -10eV bekommen, aber das ist dann was anderes…)
Wenn ein Elektron von einer Bahn auf eine andere “springt”, dann ändert sich seine Energie entsprechend sprunghaft. Deswegen sprach man dann auch vom “Quantensprung”. Das Wort “Quant” wurde jetzt also nicht mehr für ein Energiepaket selbst verwendet, sondern wurde im Begriff “Quantisierung” auf die Energien eines Elektrons übertragen.
Ein Grund, warum das sinnvoll war, ist der, dass in den Formeln, die diese Bahnen beschreiben, das Plancksche Wirkungsquantum steckte. (Auf Basis dieser Annahme hatte Arthur Erich Haas auch schon ein Atommodell entwickelt, in dem die Größe h zentral war und das ein bisschen als Vorläufer für das Bohrsche Modell diente. Woran man mal wieder sieht, dass der Fortschritt in der Physik meist inkrementell ist und dass der häufige Fokus auf einige wenige Personen das verschleiert. Von Haas habe ich zumindest in diesem Zusammenhang im Studium nichts gehört.)
Aber natürlich ist die Energie eines Elektrons nicht immer quantisiert. Ein freies Elektron kann man, beispielsweise in einem elektrischen Feld, beschleunigen. Dabei sind beliebige Werte der Energie möglich, ich muss das Elektron nicht in “Energiesprüngen” beschleunigen, sondern seine Energie erhöht sich stetig. Es ist also nicht so, dass die Eigenschaften immer quantisiert werden – das ist nur manchmal der Fall. (Später konnte man dann zeigen dass man diskrete Energien bekommt, wenn ein Elektron gebunden ist, und kontinuierliche, wenn es ungebunden ist.)
Noch einmal etwa zehn Jahre später haben dann Heisenberg und Schrödinger das entwickelt, was wir heute “Quantenmechanik” nennen. Dabei wurde der Begriff der “Quantisierung” verwendet, Schrödinger beispielsweise schrieb (Quantisierung als Eigenwertproblem, Schrödinger, 1925):
In dieser Mitteilung mochte ich zunächst an dem einfachsten Fall des (nichtrelativistischen und ungestörten) Wasserstoffatoms zeigen, daß die übliche Quantisierungsvorschrift sich durch eine andere Forderung ersetzen läßt, in der kein Wort von ,,ganzen Zahlen” mehr vorkommt. Vielmehr ergibt sich die Ganzzahligkeit auf dieselbe natürliche Art, wie etwa die Ganzzahligkeit der Knotenzahl einer schwingenden Saite. Die neue Auffassung ist verallgemeinerungsfähig und rührt, wie ich glaube, sehr tief an das wahre Wesen der Quantenvorschriften.
Also: Schrödinger zeigte, dass man die “Quantisierung” der Bahnen beim Wasserstoffatom (die man mit n=1,2,3… durchnummeriert, wie wir oben gesehen haben) auf natürliche Weise als Konsequenz aus etwas anderem ergibt. Dieses “andere” war die berühmte Schrödingergleichung (zu der findet ihr bei meinen Artikelserien gleich ein 8-teiliges Mammutwerk, da wird auch genau erklärt, wie sich die “Quantisierung” auf ganz “natürliche Art” ergibt). Die Schrödingergleichung selbst enthält nicht mehr die Forderung, dass da irgendetwas diskret sein muss oder sich mit ganzen Zahlen durchnummerieren lässt. Das ergibt sich vielmehr automatisch aus der Mathematik, wenn man das Wasserstoffatom berechnet. Für andere Probleme (beispielsweise das frei herumfliegende Elektron) sagt die Schrödingergleichung ganz korrekt vorher, dass da nichts quantisiert ist.
Die “Quantisierung”, die bis dahin also als ein ganz fundamentaler Aspekt der Beschreibung von Elektronen galt, war nur eine Folgerung aus der Gleichung, mit der man die Elektronen beschreibt, und ergab sich auch nur in einigen Fällen. Eigentlich hätte man das zum Anlass nehmen können, den Begriff der “Quantisierung” oder des “Quants” zumindest aus dem Namen der Theorie herauszunehmen (man hätte zum Beispiel in Anlehnung an de Broglie die Theorie “Materiewellenmechanik” nennen können). Aber der Begriff “Quant” war zu diesem Zeitpunkt nun einmal sehr gebräuchlich und deswegen bekam die Theorie, aus der man eben auch die Quantisierung ableiten kann, den Namen “Quantenmechanik”. Man hat also den Begriff der “Quantisierung” mit einer neuen, zusätzlichen Bedeutung versehen: Wenn man eine Theorie der klassischen Physik so erweitert, dass in ihr die korrekten Regeln der Quantenmechanik gelten, spricht man von der “Quantisierung” der Theorie.
Das führt dann zu einer weiteren Quelle der Verwirrung zum Quantenbegriff: die sogenannte “zweite Quantisierung”. Das ist ein ziemlich irreführender Begriff aus der Quantenfeldtheorie (da wird nichts zweimal quantisiert), aber da ich darüber schon mal ausführlich geschrieben habe und da das auch eher was für die Fortgeschrittenen ist, kann ich mir das heute sparen. (Im Rahmen der Quantenfeldtheorie kann man dann auch verstehen, warum Quantenfelder teilchenartig aussehen.) Der Begriff “Quantenfeldtheorie” selbst entspricht aber genau der Nomenklatur, die ich gerade erklärt habe: Man nimmt die klassische Feldtheorie (die sich mit Größen beschäftigt, die an jedem Punkt des Raums definiert sind) und macht eine Quantentheorie draus.
Es kommt allerdings noch ein anderer Aspekt zum Quantenbegriff hinzu – und der führt dann wieder dazu, dass der Begriff “Quant” doch wieder etwas sinnvoller erscheint: In der Quantenmechanik beschreibt man Elektronen als eine “Welle” (mit Hilfe der sogenannten “Wellenfunktion”). Eine Welle ist ja ein ausgedehntes Objekt, das Elektron ist also gewissermaßen “verschmiert”. (Mehr zur Wellenfunktion und dem, was ich hier schreibe, findet ihr in meiner Serie zur Schrödingergleichung oder auch hier.) Wenn wir aber tatsächlich ein Elektron zu messen versuchen, dann finden wir immer ein ganzes Elektron, niemals nur ein Stück eines Elektrons. Dasselbe gilt auch zum Beispiel für Lichtquanten (darüber habe ich mal im Zusammenhang mit dem Nobelpreis 2012 geschrieben): wenn man Lichtquanten absorbiert oder emittiert, dann sind es immer ganze Quanten, niemals halbe. (Genau mit dieser Idee hat ja alles seinerzeit bei Planck und Einstein angefangen.) Insofern ist die Quantisierung (in dem Sinne, dass wir immer ganze Teilchen beobachten, auch wenn wir ihr Verhalten über Wellen beschreiben) doch auch ein zentraler Aspekt der Quantenmechanik – es ist eine Theorie mit Wellen, bei der ich aber trotzdem immer ganze Teilchen (“Quanten”) beobachte.Das gilt für alle Teilchen: Auch Quarks, Gluonen oder Higgs-Teilchen beobachtet man immer nur “ganz”, niemals bloß “halb”. (Das ist tatsächlich ein bisschen vereinfacht, weil man auch Überlagerungen von Zuständen mit unterschiedlicher Teilchenzahl haben kann, lest den Artikel zum Nobelpreis von 2012, wenn ihr mehr darüber wissen wollt.)
Dasselbe gilt auch für andere Phänomene: wenn zum Beispiel Atome schwingen, können sich Schwingungswellen bilden, ganz ähnlich wie bei einer schwingenden Seilwelle. Auch diese Schwingungswellen sind “quantisiert” – man kann nicht beliebige Energien in der Schwingung haben, sondern nur ganz bestimmte.
Der Begriff “Quant” oder “Quantisierung” hat also einige unterschiedliche Aspekte:
- Quanten sind Energiepakete, die man bei der Absorption und Emission zum Beispiel von Lichtenergie hat – abhängig von der Frequenz des Lichts kann man nur bestimmte Energiemengen absorbieren und emittieren.
- Ähnliche Quanten gibt es auch bei anderen Phänomenen, beispielsweise der Schwingung von Atomen.
- Elektronen (und andere Teilchen) haben in manchen Fällen keine beliebigen Werte der Energie, sondern es sind nur bestimmte Werte möglich (wie beim Wasserstoffatom). Die Energie dieser Teilchen ist damit “quantisiert” (und beim Übergang von einem Zustand zum anderen kann dann zum Beispiel ein Lichtquant mit dieser Energie ausgesandt werden).
- Wenn man Elementarteilchen wie Elektronen beobachtet, dann misst man immer ganze Teilchen, keine halben Elektronen oder Viertelquarks, obwohl man die Teilchen ja mit Hilfe von Wellen beschreiben kann.
- Wenn man eine Theorie von der klassischen Beschreibung in die Quantentheorische Beschreibung überführt, nennt man das die “Quantisierung” der Theorie.
Wir können diese Aspekte zum Abschluss nochmal anders betrachten, indem wir die naheliegende Laienfrage stellen: “Ist ein Elektron ein Quant”? Zunächst mal kann ein Elektron sich in einem Zustand wie beim Wasserstoffatom befinden, wo nicht beliebige Energien möglich sind – die Energie ist quantisiert und um das Elektron in einen anderen Zustand zu bringen, muss ich ihm eine bestimmte Mindestenergie zuführen weniger geht nicht. Aber das Elektron muss nicht in einem solchen Zustand sein – wenn es frei ist, kann ich seine Energie um beliebige Werte erhöhen. Auf der anderen Seite messe ich ein Elektron aber immer als ein Elektron, in dem Sinne ist es also ein Quant. (Man könnte im Rahmen der Quantenfeldtheorie sagen: Es ist eine quantisierte Anregung des Elektronfelds.) Und schließlich ist die Theorie, mit der ich das Elektron beschreibe, eine Quantentheorie und lässt sich durch “Quantisierung” aus der klassischen Mechanik ableiten.
Ihr seht, dass der Begriff “Quant” ein bisschen überfrachtet und unscharf ist. Das ist in der Physik nicht ungewöhnlich (ein anderes Beispiel ist der Begriff “Masse”), kann aber für Außenstehende verwirrend sein. Diese Verwirrung wird insbesondere dadurch gesteigert, dass populärwissenschaftlcihe Darstellungen ja typischerweise auf Formeln verzichten – damit sind die Begriffe alles, was man bekommt, und wenn diese Begriffe dann unscharf sind, macht es das Verständnis natürlich nicht einfacher. Das ist gerade beim Erklären von Physik ein echtes Problem: Einerseits will man natürlich die Begriffe so verwenden, wie es die Physikerinnen selbst tatsächlich auch tun, aber andererseits sind diese Begriffe ohne die zugehörigen Formeln eben oft verwirrend und haben unterschiedliche Aspekte, die nicht leicht auseinanderzuhalten sind. Ich hoffe, zumindest beim Quantenbegriff seht ihr jetzt etwas klarer,






Kommentare (58)