Das berühmte Doppelspalt-Experiment darf ja eigentlich in keiner Erklärung der Quantenmechanik fehlen. Leider wird bei der Darstellung häufig eine kleine, aber entscheidende Schlamperei begangen, die das Ganze wesentlich verwirrender macht. (Was nicht heißen soll, dass es nicht verwirrend ist, im Sinne von “für unseren mit klassischer Physik geschulten Verstand schwer nachvollziehbar.”)
Beim Doppelspalt-Experiment werden Elektronen oder Photonen (Lichtteilchen) durch eine Anordnung aus zwei eng nebeneinander liegenden Spalten geschickt und treffen dann auf einen Detektor-Schirm. Ist nur ein Spalt offen, sieht man auf dem Schirm hinter dem Spalt ein entsprechendes Bild hinter dem einen Spalt:

ist der andere Spalt offen, dann sieht man das Maximum hinter dem zweiten Spalt:
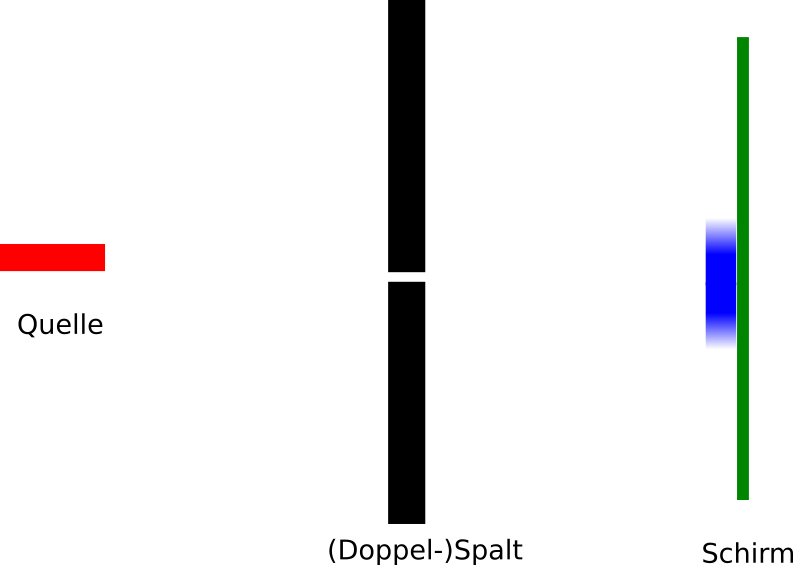
sind aber beide Schirme offen, dann sieht man nicht etwa eine einfache Überlagerung der beiden, sondern ein Interferenzmuster.
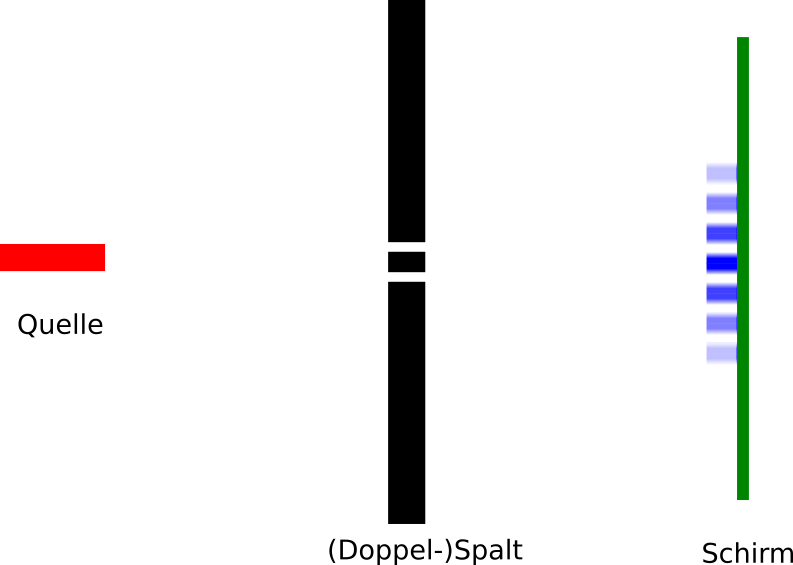
Ein solches Interferenzmuster kann man beispielsweise dadurch erklären, dass man annimmt, dass die Quelle (kohärente) Wellen aussendet, die sich dann an einigen Stellen aussenden oder verstärken, so wie dieses Bild es veranschaulicht. Die Linien darin sind die Wellenberge, dazwischen sind die Wellentäler

By inductiveload – Own work (Own drawing), Public Domain, Link
Diese Interferenz hat schon Young 1805 für Licht entdeckt. Das seltsame an der Sache ist aber, dass man auf dem Schirm trotzdem immer nur einzelne, ganze Teilchen detektiert. Selbst wenn man die Intensität soweit herunterregelt, dass zu jedem Zeitpunkt immer nur ein Photon oder Elektron unterwegs ist, bildet sich trotzdem das Interferenzmuster, obwohl man ja denken sollte, dass ein einzelnes Elektron entweder durch den einen oder durch den anderen Spalt geht und deshalb nicht interferieren kann. Man kann das Ganze in der Quantenmechanik vollkommen konsistent beschreiben – entweder nutzt man die sogenannte “Wellenfunktion” (klickt dazu rechts bei den Artikelserien auf meine Serie zur Schrödingergleichung) oder alternativ mit dem sogenannten Pfadintegral, das ich auch mal erklärt habe.
Philosophisch ist das Ganze schon recht rätselhaft – ist das Elektron nun eine Welle oder ein Teilchen? Wie kann ich den Widerspruch auflösen (der sich durch Effekte wie “Verschränkung” noch prägnanter darstellen lässt, dazu empfehle ich meine dreiteilige Serie Quantenmechanik verstehen, die ihr auch bei den Artikelserien findet)? Die Quantenmechanik stellt unser Alltagsbild der Realität durchaus in Frage, wie ich auch hier ausführlich dargestellt habe. Für eine detaillierte Diskussion empfehle ich auch das Buch “Beyond Weird” von Philipp Ball (auch wenn ich mich neulich über einen Aspekt aufgeregt habe, das Buch ist ansonsten sehr gut).
Darum soll es heute aber gar nicht gehen. Für das folgende reicht das Bild mit den Wellen vollkommen aus. Schaut es euch nochmal an. Es ist leicht einzusehen, dass der Effekt nur da auftreten kann, wo sich die beiden Einzelwellen überlagern, denn er kommt ja dadurch zustande, dass an einige Stellen Wellenberge der einen Teilweile auf Wellenberge der anderen treffen, an anderen Stellen dagegen Wellenberge auf Wellentäler. Im einen Fall verstärken sich die Wellen, im anderen löschen sie sich aus. (Das Verstärken habe ich in meinem Bild bei den Farbverläufen nicht so klar eingezeichnet.)
Wenn die beiden Spalte sehr weit auseinanderliegen, wird der Effekt also sicher verschwinden, denn dann können sich die Einzelwellen nicht mehr überlagern, weil es gar keinen Ort gibt, wo beide Einzelwellen eine nennenswerte Intensität haben. (Deswegen ist das Ganze mit Elektronen auch nicht einfach zu realisieren, denn da müssen die Spalten schon sehr schmal sein und sehr dicht zusammenliegen.)
Aber das ist genau das, was in vielen Büchern irreführend dargestellt wird. Da seht ihr oft erst ein Bild, das zeigt, was nur bei einem Spalt passieren würde:

dann das entsprechende Bild für den zweiten Spalt:

und dann, was man passiert, wenn beide Spalte offen sind:

So kann es aber nicht sein, denn wenn man die beiden Einzelbilder oben überlagert, gibt es gar keinen Bereich auf dem Schirm, der von beiden Wellen getroffen wird, also kann sich auch nichts überlagern.
Meist ist es bei diesen Artikeln oder Bildern (hier bei New Scientist , hier bei physics in a minute, ich habe hier auch ein Schulbuch herumliegen, wo so ein Bild verwendet wird) so, dass zuerst erklärt wird, wie sich klassische Teilchen verhalten. Dann sieht das Bild zunächst so aus:
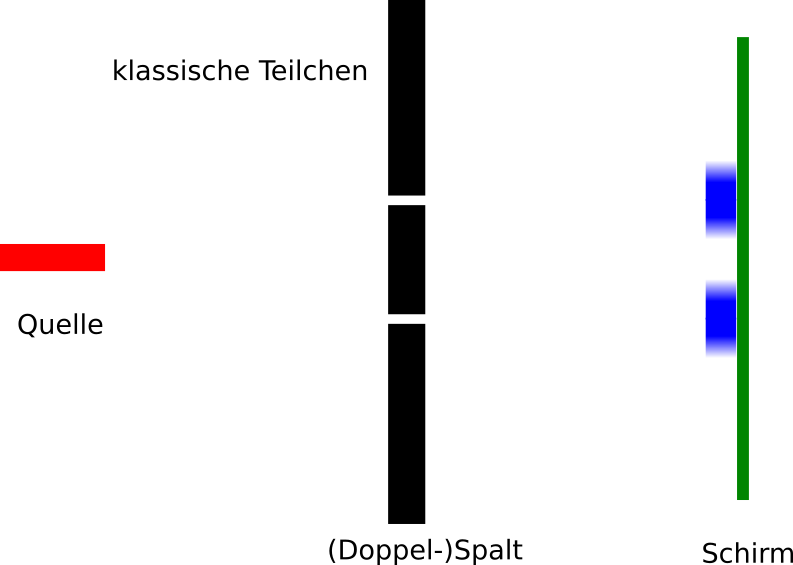
und danach wird das Bild mit dem Doppelspalt und der Interferenz gezeigt wie gerade eben.
Das ist dann nicht wirklich falsch, aber immer noch irreführend. Wen sich die Teilchen wirklich vollkommen wie klassische Teilchen verhalten und einfach nur gerade durch einen Spalt fliegen können, bekomme ich natürlich das Bild mit zwei klar getrennten Maxima (solange der Abstand zwischen den Spalten groß genug ist). Wenn ich dann aber den Übergang zu Wellen (oder quantenmechanischen Objekten mache), dann müsste ich auch nochmal zeigen, dass dann das Muster sich schon bei einem Einzelspalt verbreitert (weil es bei Wellen so ist, dass sich jeder Einzelspalt wie eine kleine Lichtquelle verhält, so wie das auch oben im Wellenbild gezeichnet wurde):

(Das zweite Bild zu malen, erspare ich mir, ebenso den Aspekt, dass eine Welle am Einzelspalt auch Beugung erfahren könnte.)
Also: Nur wenn ein Bereich existiert, der von jedem der Spalte erreicht werden kann, wenn nur dieser geöffnet ist, kann es auch Interferenz in diesem Bereich geben. Wenn die Muster der Einzelspalte räumlich getrennt sind, dann überlagert sich auch nichts. (Hinweis für die Expertinnen: Das muss auch so sein, denn man könnte ja zum Beispiel eine Welcher-Weg-Information abspeichern, dann muss sich das klassische Überlagerungsmuster ergeben, wenn ich die Information aber mit einem Quantenradierer vernichte, muss sich wieder das Interferenzbild als Summe der beiden Teile ergeben.) Feynman macht es in den Feynman Lectures übrigens (natürlich) richtig und erklärt extra, dass ein Teilchen (etwas militaristisch als Gewehrkugel illustriert) an den Wänden der Spaltöffnung abprallen kann und deshalb in alle Richtungen fliegt: “A bullet which happens to hit one of the holes may bounce off the edges of the hole, and may end up anywhere at all”.
Wenn ihr aber die Bilder für die Einzelspalte so zeichnet, dass die Muster auf dem Schirm vollkommen getrennt sind, dann ist es vollkommen unverständlich, warum sich dann in der Mitte, die dann ja gar nicht erreicht werden kann, plötzlich ein Maximum bilden soll. Man suggeriert damit, dass die Quantenmechanik noch viel mysteriöser ist – es kann dann scheinbar einen Effekt an einem Ort geben, an dem die Teilchen gar nicht sein können, wenn man einfach nur die Einzelbilder überlagert.
Wie gesagt, meist ist es so, dass zunächst von klassischen Teilchen am Doppelspalt gesprochen wird, die dann zwei deutlich getrennte Maxima erzeugen, dann kommt direkt der Übergang zur Quantenmechanik (so auch z.B. bei dieser Seite der LMU München). Das ist dann nicht wirklich falsch, aber es unterschlägt, dass eben schon bei einem Spalt der Impuls verbreitert wird, wenn man vom Teilchen zur Welle (oder zur Quantenmechanik) übergeht. Irreführend ist es in meinen Augen auf jeden Fall – wenn ihr also solche Darstellungen seht (oder selbst so etwas erklärt), dann achtet am besten darauf, es klarer zu machen.
PS: Falls ihr weitere Beispiele findet, hinterlasst gern links in den Kommentaren.






Kommentare (101)