Warum sind Dinge eigentlich nie an zwei Orten gleichzeitig?
Klingt wie eine dumme Frage? In unserer Alltagserfahrung ist es das natürlich auch – mein Stift liegt vor oder hinter meinem Bildschirm, aber nicht beides gleichzeitig – wie soll das auch gehen?
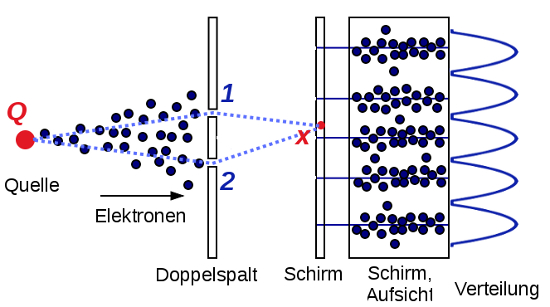
In der Quantenmechanik sieht die Sache aber anders aus: Dort haben Objekte (wenn wir sie nicht gerade “messen”, dazu komme ich noch) eine Wahrscheinlichkeit, dafür, an einem bestimmten Ort zu sein, aber auch nicht mehr. Nehmen wir mal wieder das berühmte und klassische Experiment der Quantenmechanik, den Doppelspalt-Versuch: Wir schießen einzelne Elektronen auf zwei schmale, eng beieinander liegende Spalte, dann bekommen wir dahinter nach einer Weile ein Muster aus hellen und dunklen Streifen:
(Bild gemeinfrei, modifiziert von Wikipedia.)
Jedes einzelne Elektron trifft auf den Schirm und kann dort gemessen (detektiert) werden. Man kann das Muster dadurch erklären, dass das Elektron eine Wahrscheinlichkeit dafür hat, durch den einen oder anderen Spalt zu laufen und dass diese beiden Möglichkeiten hinter dem Doppelspalt miteinander wechselwirken, so dass sich einige Möglichkeiten auslöschen, andere verstärken. (Ich erkläre das hier sehr verkürzt; mehr dazu findet ihr in diesem Artikel oder auch hier.)
Man sagt auch, dass sich das Elektron in einem Überlagerungszustand befindet. Praktischerweise habe ich Überlagerungszustände in einem meiner letzten Blogartikel erklärt (der schon sehr lange her ist – leider komme ich im Moment kaum zum Bloggen, zu viele andere Dinge und Hobbies interferieren da, und irgendwie sind es die Blogartikel, die da immer das Minimum der Wahrscheinlichkeit erwischen…)
Elektronen können also in einem Überlagerungszustand sein, beispielsweise einer Überlagerung aus “Elektron geht durch den oberen Spalt” und “Elektron geht durch den unteren Spalt”, und dass es solche Überlagerungszustände gibt, können wir nachweisen, indem wir Interferenzexperimente machen.
Jetzt könnte man sagen “Ja, o.k., das sind halt Elektronen, die genügen den seltsamen Regeln der Quantenmechanik (kurz QM), die gelten halt für klassische Objekte wie Stifte einfach nicht.” Fragt sich nur: Warum nicht? Denn auch der Stift besteht ja aus Elektronen (und Quarks und Gluonen in den Atomkernen), die den Regeln der QM genügen. Was sorgt also dafür, dass Stifte trotzdem nie in einer Überlagerung aus “hier” und “da” sein können?
Es kann nicht einfach so sein, dass die Regeln der QM irgendwann “aufhören” – beispielsweise, wenn Objekte zu groß oder zu schwer werden, denn es gibt makroskopisch direkt beobachtbare Quantenphänomene. In einem Supraleiter beispielsweise sind sehr viele Elektronen alle im selben Zustand und verhalten sich wie ein großes Quantenobjekt; in einem Laserstrahl haben wir eine komplexe Überlagerung von Zuständen mit unterschiedlich vielen Photonen (Ein bisschen habe ich das hier erklärt.) Und inzwischen schafft man es, auch an ziemlich großen Objekten die Überlagerung durch Interferenzen nachzuweisen, beispielsweise an Molekülen.
Ein weiterer Grund, warum die QM nicht einfach irgendwann “aufhören” kann zu gelten, wenn wir zu großen Objekten übergehen, ist der, dass die klassische Physik ja eine Konsequenz der QM sein sollte – die QM ist eine grundlegendere Theorie, die die klassische Physik umfasst. Da ist es doch zumindest seltsam, dass Quanteneffekte so empfindlich sein sollen, dass sie quasi sofort verschwinden, sobald man etwas größere Objekte anguckt.
Guckt man genauer hin, sind es eigentlich zwei leicht unterschiedliche Fragen, die wir hier stellen:
- Warum beobachten wir keine Interferenzphänomene an makroskopischen Objekten?
- Warum beobachten wir Objekte immer nur in bestimmten (“klassischen”) Zuständen (bei makroskopischen Objekten sind das bevorzugt Ortszustände)?
Und eng damit verwandt ist das größte offene Rätsel der QM, dass Messproblem:
3. Was passiert bei einer Messung? Wie (und warum) wird aus “Wahrscheinlichkeit” “Gewissheit”?
Die ersten beiden Fragen können (weitgehend) durch ein physikalisches Phänomen erklärt werden, dass man erst seit den 70er und 80er Jahren (des 20. Jh) so richtig untersucht, die so genannte “Dekohärenz”. Einige Leute behaupten auch, dass die Dekohärenz die 3. Frage beantwortet und das Messproblem löst, aber das ist [meiner Ansicht nach] falsch.
Was “Dekohärenz” ist? Das schauen wir uns jetzt ausführlich an. (Hinweis: Das meiste, was ich hier schreibe, habe ich aus dem Artikel von Schlosshauer, s.u., auch das Buch “Beyond Weird” ist sehr zu empfehlen, es ist allerdings an einigen Stellen etwas schwammig. Ich empfehle auch unbedingt, bei Sabine Hossenfelders backreaction-Blog vorbeizuschauen, sie erklärt das Ganze etwas anders, aber auch sehr klar.)
Interferenzen
Schauen wir noch einmal auf das Elektron am Doppelspalt: Es kann beide Wege gehen, befindet sich also hinter dem Doppelspalt in einer Überlagerung aus beiden Möglichkeiten, und diese Überlagerung führt zur Interferenz. Bezeichnen wir die beiden Möglichkeiten – wie in der QM üblich – mit Zuständen, die wir in seltsame Klammern einschließen:
|oben> für den Zustand, wo das Elektron durch den oberen Spalt geht und
|unten> für den Weg durch den unteren Spalt.
Das Elektron ist jetzt – da es für beide Spalte dieselbe Wahrscheinlichkeit hat, im Zustand
|oben> + |unten>
(wobei ich mir eigentlich notwendige mathematische Normierungsfaktoren spare. Wer’s genau wissen will, kann bei den Artikelserien klicken und meine Serie “Quantenmechanik verstehen” lesen.)
Die Regeln der QM (In der QM-verstehen-Serie detailliert erklärt) sagen uns jetzt, dass wir, um die Wahrscheinlichkeiten zu berechnen, diesen Ausdruck mit sich selbst multiplizieren müssen. Irgendwann in der Schule habt ihr mal die binomischen Formeln gelernt: (a+b)²=a² + 2ab + b².
Das geht hier genauso, nur dass man (aus Gründen…) statt (|oben>)² was anderes schreibt, nämlich <oben|oben>. Dann bekommen wir also (mit ziemlich viel mathematischer Schlampigkeit, weil ich auch eigentlich das Betragsquadrat für komplexe Zahlen nehmen müsste und so, aber darauf kommt es hier zum Glück nicht an):
<oben | oben> + 2 <oben | unten> + <unten | unten>
Wie kann man diese Formel interpretieren? Sie gibt die Wahrscheinlichkeit an, dass ein bestimmter Punkt auf dem Schirm vom Elektron getroffen wird. An den Punkten, die man nur auf dem Weg über den oberen (oder den unteren) Spalt erreichen kann (wenn es solche gibt) ist nur der erste (oder letzte) Term ungleich Null und man merkt von dem jeweils anderen Spalt nichts.
Anders sieht es an den Punkten aus, die auf beiden Wegen erreicht werden können: Dort gibt es drei Terme, der erste entspricht dem, was man auch in der klassischen Physik erwarten würde, wenn das Teilchen den oberen Weg geht, der dritte dem klassischen Ergebnis für den unteren Weg. Das Gesamtergebnis ist aber nicht einfach die Summe aus diesen beiden, denn es gibt ja auch noch den Term in der Mitte: Wir sehen, dass wir einen Ausdruck haben, in dem die Zustände oben und unten gemischt auftreten, und genau der ist für die Interferenz verantwortlich. Interferenz gibt es also genau an den Punkten auf dem Schirm, die von einem Elektron auf beiden Wegen erreicht werden können.
(Ich spare mir hier sehr viele Details, weil es heute auf die nicht so ankommt; wer es genauer wissen will, kann die oben verlinkten Artikel lesen oder einen Blick in die Feynman Lectures riskieren; Feynman erklärt das sehr ausführlich, allerdings mit ein wenig mehr Mathematik.)
Wir können das Interferenzmuster aber zerstören, wenn wir das Elektron beobachten. Wenn wir beispielsweise einen der beiden Spalte mit einem Laser bestrahlen, dann wechselwirken die Photonen mit dem Elektron, wenn es durch diesen Spalt geht, aber nicht, wenn es durch den anderen Spalt geht. Wir können uns (nicht super-realistisch, aber konzeptionell einfach) beispielsweise vorstellen, dass das Elektron ein Photon ablenkt und es zur Seite ablenkt, so dass es in einen Detektor fliegt.
Wir müssen jetzt die Photonen mit in das Spiel mit einbeziehen. Nehmen wir an, der Laser bestrahlt den oberen Spalt. Ich nenne den Zustand, wo die Photonen nicht durch das Elektron beeinflusst werden (weil das Elektron den unteren Weg genommen hat)
|p ungestört>
und den, wo das Elektron von den Photonen getroffen wird und eins der Photonen deshalb am Elektron gestreut wird
|p gestört>.
Wir haben jetzt hinter dem Spalt den Zustand
|oben> |p gestört> + |unten> |p ungestört>.
Nach der gleichen Logik wie eben müssen wir jetzt wieder das Quadrat dieses Ausdrucks bilden, um zu sehen, ob es Interferenzeffekte gibt. Wir bekommen damit
<oben | oben> <p gestört | p gestört> + 2 <oben | unten> <p gestört | p ungestört> + <unten | unten> <p ungestört | p ungestört>
Der erste und der dritte Term entsprechen dabei dem, was wir auch in der klassischen Physik hätten – der erste steht für den Fall, dass das Elektron den oberen Weg geht und die Photonen stört, der letzte für den Fall, dass das Elektron den unteren Weg geht und die Photonen nicht stört.
In der Mitte haben wir jetzt wie vorher <oben | unten> , zusätzlich aber multipliziert mit <p gestört | p ungestört>. Und dieser zweite Ausdruck ist gleich Null.Warum? Er entspricht der Interferenz zwischen dem gestörten und dem ungestörten Laserstrahl. Da wir aber im gestörten Laserstrahl ein Photon in eine ganz andere Richtung abgelenkt haben, können diese beiden Möglichkeiten gar nicht interferieren. (Mathematisch genauer: Da wir das nicht beobachten, müssen wir hier über die beiden Zustände komplett integrieren, und solange sie orthogonal sind, ist das Ergebnis Null.)
Häufig wird das anders ausgedrückt: Durch die Wechselwirkung mit dem Photon haben wir jetzt eine “Welcher-Weg-Information”, das heißt, wir wissen (oder können es zumindest prinzipiell wissen), welchen Weg das Elektron gegangen ist, dazu müssen wir ja nur schauen, ob ein Photon gestreut wurde oder nicht. Die Zustände |p gestört> und |p ungestört> sind direkt und eindeutig unterscheidbar, damit wissen wir, welchen Weg das Elektron gegangen ist. Dabei ist es übrigens nicht entscheidend, ob wir tatsächlich hingucken oder nicht – wenn das gestreute Photon auf eine Wand fällt und da absorbiert wird, ist das auch in Ordnung, denn prinzipiell könnten wir ja sehen, dass die Wand Energie vom Photon bekommen hat.
Falls ihr jetzt überlegt “Aber Moment mal, Photonen sind doch auch Quantenobjekte, könnte ich die beiden Photonen nicht mit ein paar geeigneten Spiegeln wieder zusammenführen, so dass sie doch miteinander interferieren könnten?”, dann habt ihr recht. Das kann man tun, und sobald ihr das so tut, dass der resultierende Zustand für die beiden Photonen nicht mehr eindeutig erkennen lässt, welchen Weg die Photonen genommen haben, ist das Interferenzmuster auch wieder da. Das wird später noch wichtig werden, aber auf die Details, wie man das genau macht (und wie alles logisch konsistent bleibt, wenn man die Photonen vielleicht erstmal irgendwo speichert und erst später entscheidet, ob man sie interferieren lässt oder nicht) gehe ich hier nicht ein. Wer dazu mehr wissen will, dem empfehle ich das Buch “Einsteins Schleier” von Zeilinger, der beschreibt einen ganzen Haufen sehr abgefahrener Quantenexperimente, die genau solche Tricks ausnutzen. Oder ihr googelt mal nach “Quantenradierer”.
Und falls ihr gerade überlegt, dass die beiden möglichen Zustände für das Photon (gestreut oder nicht gestreut) ja vielleicht nicht perfekt unterscheidbar sein könnten (vielleicht nehmen wir ein Photon, das nur ganz wenig gestreut wird) – ja, dann bekommt ihr ein teilweises Interferenzmuster. So was nennt man dann eine “schwache Messung”, aber darauf gehe ich heute nicht weiter ein. (Ein bisschen was dazu steht aber in diesem Artikel.)
Dekohärenz
Falls euch das eben zu detailliert war, hier die gute Nachricht: Entscheidend an dem Beispiel mit der Interferenz ist nur eins: Sobald euer Objekt, dessen Interferenz ihr beobachten wollt, mit anderen Objekten wechselwirkt, könnt ihr die Interferenz nicht mehr beobachten, weil der Zustand eures Objekts jetzt mit dem der anderen Objekte verknüpft ist. Diese “Verknüpfung” ist übrigens nichts anderes als ein Beispiel für die berühmte quantenmechanische Verschränkung. Durch den Laser habt ihr den Zustand eures Elektrons mit dem der Photonen verschränkt, und damit könnt ihr jetzt nicht mehr ohne Weiteres Interferenzen des Elektronzustands beobachten, weil dazu auch die verschränkten Teilchen passend interferieren müssten. (Ein wichtiges paper zum Thema hat deshalb auch den Titel “Destruction of interference by entanglement”.)
Und jetzt kommen wir endlich zur Dekohärenz. Stellt euch ein makroskopisches Objekt vor, an dem ihr ein Interferenzexperiment machen wollt; vielleicht so etwas wie einen Ball. Nehmt an, der Ball wäre in einem Überlagerungszustand aus zwei Positionen, hier und da. (So wie die beiden Wege oben und unten durch den Spalt.) Der Ball ist groß, er wird ständig von Luftmolekülen getroffen, absorbiert Photonen und wechselwirkt damit auf verschiedenste Weise mit jeder Menge anderer Teilchen. Diese Wechselwirkung ist “hier” anders als “da”, weil die Luftmoleküle eben “hier” auf den Ball treffen und abgelenkt werden, wenn er “hier” ist, und “da”, wenn er “da” ist.
Es passiert jetzt genau dasselbe wie bei unserem Elektron: Um eine Interferenz der beiden Zustände des Balls zu bekommen, müssten auch die Zustände all dieser Luftmoleküle, Photonen und so weiter miteinander interferieren können, und das ist bei der Vielzahl an Wechselwirkungen natürlich vollkommen unmöglich.
Weil der Ball mit der Umwelt wechselwirkt und sein Zustand dabei mit allen möglichen anderen Teilchen verschränkt wird, ist eine Interferenz nicht mehr möglich. Zustände, die interferieren können, nennt man manchmal auch “kohärent”, und diese “Kohärenz” geht verloren. Deshalb heißt das Ganze “Dekohärenz”.
Das klärt also unsere erste Frage von oben: Makroskopische Objekte können keine Interferenz zeigen, weil sie immer mit der Umgebung wechselwirken und dadurch mit ihr verschränkt werden. Deshalb muss man bei Experimenten, die Interferenz an Molekülen zeigen sollen (siehe oben) auch sicherstellen, dass es möglichst wenig Störeinflüsse aus der Umgebung gibt, ansonsten funktioniert es nicht. Wie groß ein Objekt maximal sein kann, um noch Interferenz zu zeigen, hängt damit davon ab, wie gut ihr das Objekt von allen Störeinflüssen isolieren könnt.
Diese Überlegung beantwortet auch noch eine weitere Frage, die ich oben aufgeworfen habe: Wieso verschwinden Quanteneffekte bei makroskopischen Objekten sofort? Sie tun das gar nicht wirklich, im Gegenteil: Der Quantenzustands eures makroskopischen Objekts wird mit allen möglichen anderen Objekten quantenmechanisch verschränkt, die Quantennatur verschwindet also nicht, im Gegenteil, sie breitet sich über die gesamte Umgebung aus. Diese Ausbreitung verhindert aber, dass ihr an dem Objekt selbst noch Interferenzphänomene beobachten könnt (alle gemischten Terme wie <oben|unten> werden mit unglaublich vielen weiteren Termen multipliziert, die alle praktisch Null sind), weil ihr dazu die gesamte Umgebung mit einbeziehen müsstet. Um mich mal selbst zu zitieren:
“Alle diese Verschränkungen werden verloren sein, wie Tränen im Regen….”.
Klassische Zustände
O.k., makroskopische Objekte können also keine Interferenzerscheinungen zeigen, weil sie sich durch Wechselwirkung mit der Umgebung verschränken. Das erklärt, warum wir an makroskopischen Objekten nur selten Quanteffekte direkt beobachten können. (Was nicht heißen soll, dass Quanteneffekte im Alltag nicht wichtig wären, siehe z.B. hier, hier und hier.)
Es erklärt aber nicht, warum die Zustände, die wir beobachten, typischerweise Zustände sind, bei denen sich Objekte an einem bestimmten Ort befinden, und nicht Überlagerungszustände aus zwei Unterschiedlichen Positionen. Rein aus Sicht der Quantenmechanik zeichnet Ortszustände nichts aus gegenüber anderen Zuständen, |hier> oder |da> sind genau so gute und legale Zustände wie |hier>+|da> (oder sogar |hier>-|da>), wie ich auch in meinem Überlagerungsartikel schon erklärt habe.
Auch hier ist die Dekohärenz verantwortlich. Zustände, die wir an einem makroskopischen Objekt beobachten, sind stabil, das heißt, sie sollten sich durch Wechselwirkung mit der Umwelt nicht (stark) ändern. Nehmen wir an, wir fangen mit einem Quantenzustand an, der eine Überlagerung aus zwei Ortszuständen ist. (Man spricht gern von “pointer states”, also “Zeigerzuständen”, weil man sich vorstellt, man hätte einen Zeiger, der uns Auskunft über einen Quantenzustand geben soll.) Am Anfang kann der Zustand noch mit sich selbst interferieren, aber dann kommen, wie oben erklärt, die Wechselwirkungen ins Spiel, die diese Möglichkeit der Interferenz zerstören.
Man kann sich jetzt fragen: “Was wird dann durch diese Vielzahl an Wechselwirkungen aus dem anfänglichen Überlagerungszustand?” Die Wechselwirkungen mit den vielen Gasatomen sind, wie erklärt, für die beiden Zustände unterschiedlich und sorgen für eine komplizierte Verschränkung mit der Umwelt. Der Zustand verändert sich dadurch immer weiter.
Erreichen wir irgendwann einen stabilen Punkt, wo sich der Zustand nicht mehr nennenswert ändert? Ja, das tun wir. Die Wechselwirkungen mit der Umwelt hängen vom Ort ab (weil Atome um so stärker wechselwirken, je näher sie sich kommen; weit entfernte Atome merken nicht viel voneinander.) Damit die Wechselwirkungen unserem Zustand nicht mehr viel anhaben können, muss dieser Zustand genau so sein, dass die vielen weiteren Wechselwirkungen sich sozusagen herausmitteln.
(Hinweis für die Fortgeschrittenen: Mathematisch lässt sich das relativ leicht und weniger schwammig erklären: Der Zustand kann trotz Wechselwirkungen mit der Umwelt nur stabil sein, wenn der zugehörige Projektionsoperator zu diesem Zustand mit dem Hamilton-Operator für die Wechselwirkung mit der Umwelt kommutiert. Da diese Wechselwirkungen vom Ort abhängen, kommutiert der Hamilton-Operator der Wechselwirkung mit der Ortsraum-Basis, also sind das auch die passenden Zeigerzustände. Schlosshauer erklärt das genau auf diese Weise.)
Noch mal etwas konkreter: Wir fangen mit einem Überlagerungszustand an, beispielsweise
|hier> + |da>
Die vielen Stöße mit der Umwelt führen dazu, dass dieser Zustand sich mit der Umwelt verschränkt und nicht mehr interferieren kann. Der |hier>-Zustand und der |da>-Zustand sind jetzt jeweils mit dem Zustand der Umwelt verschränkt, und die jeweiligen Zustände der Umwelt unterscheiden sich deutlich voneinander. Genau das zeichnet die Ortszustände aus – sie sind die Zustände, bei denen sich die Verschränkungen mit der Umwelt deutlich unterscheiden, bei Zuständen wie
|hier> + |da> oder |hier> – |da>
ist genau das nicht der Fall.
Die bevorzugten Zustände, die wir beobachten, sind also die, bei denen die Zustände der Umwelt sich unterscheiden, und das sind im wesentlichen Ortszustände, weil Gasatome entweder hier oder da auf unseren Zeiger treffen.
Wahrscheinlichkeiten
Weil es so viele Stöße mit der Umwelt gibt und diese Stöße keiner Regel folgen (Gasmoleküle purzeln ja chaotisch durch die Gegend), sind die Verschränkungen mit der Umwelt ziemlich chaotisch. Natürlich haben wir keine Chance, diese ganzen chaotischen Zustände im einzelnen nachzuverfolgen. Können wir trotzdem Aussagen über den Zustand machen?
Ja, das können wir. Dazu muss man sich erinnern, dass wir in der Quantenmechanik ja eigentlich nur von Wahrscheinlichkeiten (oder genauer “Wahrscheinlichkeitsamplituden”) reden können. Hier gibt es jetzt eine relativ einfache Regel: Wenn wir einen verschränkten Zustand haben, bei dem wir nur einen Teil beobachten können, dann müssen wir über alles, was wir nicht beobachten, mitteln. (Mathematisch kann man das mit der sogenannten Dichtematrix einsehen, das erklärt Sabine Hossenfelder im oben verlinkten Artikel perfekt.)
Wir fangen also an mit dem Zustand
|hier> + |da>
Dieser verschränkt sich jetzt (durch die Stöße mit Gasatomen, Wechselwirkung mit Photonen und so weiter) mit der Umwelt, ich schreibe das mal so
|hier> |Gasmoleküle stoßen hier> +
|da> |Gasmoleküle stoßen da>
Um jetzt die Wahrscheinlichkeiten der beiden Zustände |hier> und |da> zu sehen, können wir die Logik anwenden, die wir schon beim Doppelspalt gesehen haben. Die Zustände |Gasmoleküle stoßen hier> und |Gasmoleküle stoßen da> können aber nicht miteinander interferieren (genau wie beim Doppelspalt die beiden Zustände der Photonen), so dass wir keine gemischten Terme bekommen. Wir können das (mathematisch nicht so ganz korrekt, sondern eher symbolisch zu verstehen) so schreiben:
<hier|hier> <Gasmoleküle stoßen hier|Gasmoleküle stoßen hier> + <da|da> <Gasmoleküle stoßen da|Gasmoleküle stoßen da>
Weil wir den Zustand der Gasmoleküle aber ja nicht beobachten, müssen wir über alle Möglichkeiten für diese Zustände mitteln; dabei kommt für beide Möglichkeiten |hier> und |da> dasselbe heraus.
Am Ende landen wir deshalb bei einer Situation, die wir so schreiben können:
<hier|hier> + <da|da>,
weil die ganze Mittelung über die Gasatome für beide gleich ist (und irgendwelche konstanten Faktoren ignoriere ich hier ja ohnehin).
Wir können das interpretieren als einen ganz klassischen Zustand, der eine Wahrscheinlichkeit von 50% für |hier> hat und von |50%> für da – welcher der beiden Fälle eintritt, wissen wir nicht, aber Zufälle sind in der QM ja nichts besonderes.
Ist das Messproblem gelöst?
Auf den ersten Blick sieht es jetzt so aus, als hätten wir damit den heiligen Gral der QM gefunden – aus einem anfänglichen quantenmechanischen Überlagerungszustand ist etwas geworden, das rein klassische Wahrscheinlichkeiten hat, die nur darauf beruhen, dass wir nicht alles über unser System wissen. Haben wir damit das Messproblem gelöst?
Klare Antwort: Nein. (Ja, es gibt Leute, die das anders sehen, aber ich lehne mich jetzt mal weit aus dem Fenster und sage kategorisch: Diese Leute irren sich.)
Ich habe bei diesem Argument nämlich ein bisschen getrickst und geschummelt. Ich habe (korrekt) argumentiert, dass an aus der Verschränkung mit der Umwelt und unserer Unkenntnis über diese Umwelt eine klassische Wahrscheinlichkeit bekommt.
Aber unsere Unkenntnis der Umwelt ist ja nichts Fundamentales, sondern genau das: unsere Unkenntnis. Wenn wir den Zustand eines Quantensystems nicht genau kennen, dann müssen wir über die Möglichkeiten in diesem System mitteln (und das geht mathematisch mit der Dichtematrix). Aus Verschränkung und Unkenntnis ergibt sich damit genau die klassische Wahrscheinlichkeit.
Aber in der Natur gibt es keine “Unkenntnis” – die Tatsache, dass wir nicht in der Lage sind, über die Zustände aller Gasmoleküle usw. Bescheid zu wissen, heißt ja nicht, dass die nicht eindeutige Zustände haben.
Schauen wir nochmal auf den Doppelspalt: Wenn wir eine Wechselwirkung mit einem Photon haben, dann sehen wir kein Interferenzmuster auf dem Schirm mehr. Ich hatte aber dazugesagt, dass es prinzipiell möglich wäre, die beiden Möglichkeiten für unser Photon (gestreut oder nicht gestreut) am Ende wieder so zusammenzuführen, dass wir die beiden Möglichkeiten nicht mehr unterscheiden können (das ginge zum Beispiel mit einem so genannte Interferometer), und dann ist das Interferenzmuster auch wieder da.
Prinzipiell ginge das auch für unser makroskopisches System – theoretisch ist es denkbar, all die Zustände der Gasatome, die sich bei Streuung |hier> und |da> unterscheiden, wieder so zusammenzuführen, dass eine Interferenz dieser Zustände wieder möglich ist, und dann landen wir auch wieder bei unserem Zustand |hier>+|da>.
Praktisch ist das nicht möglich, deshalb bekommen wir für alle praktischen Zwecke niemals solche Interferenzen (was nebenbei bemerkt der Sargnagel für alle Ideen von “Quantenheilung”, “Homöopathie beruht auf Quantenverschränkungen” etc. ist). Aber theoretisch gibt es keinen Punkt, ab dem das wirklich absolut und kategorisch unmöglich ist.
Wir haben es hier mit zwei unterschiedlichen Wahrscheinlichkeitsbegriffen zu tun. Die klassische Wahrscheinlichkeit ist die, die es schon in der klassischen Physik gab: Auch wenn diese vollkommen deterministisch ist, sorgt unsere Unkenntnis aller Gegebenheiten dazu, dass beim Werfen einer Münze oder eines Würfels das Ergebnis zufällig ist.
Die Quantenmechanische Wahrscheinlichkeit ist (soweit wir wissen – es könnte natürlich eine fundamentalere Theorie geben, die die Wahrscheinlichkeiten erklärt) etwas anderes: Wenn wir ein Objekt in einem Überlagerungszustand haben und messen, dann wissen wir hinterher, in welchem Zustand es ist. Vorher hatten wir eine Wahrscheinlichkeit, hinterher haben wir Gewissheit, aber die Wahrscheinlichkeit beruhte eben nicht auf einer bloßen Unkenntnis, sondern ist fundamentaler. Dass das so ist, zeigt genau unser Elektron am Doppelspalt: Wenn wir es mit unserem Laser messen, indem wir seinen Zustand mit dem des Photons verschränken (und das Ganze nicht wieder durch Interferenz zunichte machen), dann wissen wir, wo das Elektron war, aber wenn wir es nicht messen, dann zeigt die Interferenz am Doppelspalt, dass es eben nicht eindeutig am einen oder anderen Spalt war.
(Anmerkung: Naja, theoretisch ist es denkbar, dass es das doch war und dass wir das nur fundamental nicht wissen können, es gibt Interpretationen der QM, die das möglich machen, beispielsweise die deBroglie-Bohm-Theorie, aber diese fiese Pandora-Büchse mache ich heute nicht auf…)
Jetzt könnte natürlich jemand einwenden “Moment. Wenn ich das Photon messe, indem ich gucke, ob es vom Elektron aus der Bahn geworfen wurde, lande ich dann nicht auch in einem Überlagerungszustand? Wäre es nicht theoretisch möglich, auch meinen Zustand wieder durch Interferenz so zusammenzuführen, dass hinterher wieder beide Möglichkeiten da sind und ich den Zustand des Photons nicht mehr kenne?” Gute Frage. Wir wissen, dass wir so etwas nicht beobachten, deshalb haben wir das Konzept der Messung ja überhaupt eingeführt (mehr dazu in diesem Artikel). Die QM soll die Welt so beschreiben, wie wir sie durch unsere Erfahrungen und Messungen vorfinden – und da sehen wir eben, dass wir so etwas nie beobachten und dass wir das Photon entweder sehen oder nicht. (Falls jemand jetzt auf die Viele-Welten-Theorie verweist – die löst das Problem nicht wirklich, ich verweise hier mal wieder auf den backreaction-Blog. Das Buch “Beyond Weid” ist dazu auch sehr zu empfehlen.)
Entscheidend ist hier also Folgendes: Die Dekohärenz (die Wechselwirkung unserer Objekte mit der Umwelt) sorgt für alle praktischen Zwecke dafür, dass wir über den unbekannten Zustand der Umwelt mitteln müssen, und das liefert uns eine klassische Wahrscheinlichkeit. Fundamental haben wir es aber immer mit Quantenzuständen zu tun, und deren Wahrscheinlichkeiten sind konzeptionell etwas anderes. Das Messproblem bleibt ungelöst.
Fazit
Das Konzept der Dekohärenz ist – daran besteht kein Zweifel – ein großer Sprung vorwärts für das Verständnis der QM. Die Verschränkungen mit der Umwelt, die wir bei makroskopischen Objekten gar nicht vermeiden können, sorgen dafür, dass wir an solchen Objekten keine quantenmechanischen Interferenzerscheinungen beobachten können. Weil die Wechselwirkung mit der Umwelt davon abhängt, so die Objekte sind, sind Zustände, in denen Objekte an einem Ort sind, gegenüber anderen Zuständen bevorzugt. Wichtig ist dabei, dass die Dekohärenz zeigt, dass es eben nicht so ist, dass Quanteneffekte bei großen Objekten verschwinden. Im Gegenteil – makroskopische Objekte sind in unglaublich komplexer Weise mit der Umwelt quantenmechanisch verschränkt, aber gerade das führt dazu, dass wir von diesen Quanteneffekten nichts merken.
Damit erklärt uns die Dekohärenz einiges darüber, warum unsere makroskopische Welt so aussieht, wie sie es tut.
Das Messproblem bleibt allerdings ungelöst.
Quellen:
M. Schlosshauer Quantum decoherence






Kommentare (53)