Wie bewegen sich die Himmelskörper? Das ist eine Frage, die uns Menschen schon fast von Anfang an beschäftigt. Zuerst aus eher mystisch-religiösen Gründen, weil wir in den Lichtern am Himmel Symbole unserer Götter gesehen haben und aus ihrer Bewegung die Zukunft vorhersagen wollten. Später war es dann der Wunsch, das Universum aus wissenschaftlicher Sicht zu verstehen. Und bis heute haben wir diese Frage noch nicht vollständig beantwortet. Das sogenannte Dreikörperproblem zeigt sehr gut, wie viel wir einerseits schon heraus gefunden haben und wie komplex dieses Thema andererseits ist.
Die moderne Himmelsmechanik, wie die Wissenschaft von der Bewegung der Himmelskörper heißt, begann im Prinzip mit Johannes Kepler. Zu Beginn des 17. Jahrhunderts stellte er die ersten mathematischen Regeln auf, die beschrieben wie sich Planeten um die Sonne bewegen. Ein paar Jahrzehnte später lieferte Isaac Newton dann einen detaillierten mathematischen Unterbau für die Gesetze von Kepler und erklärte, wie man die Gravitationskraft berechnen kann, die zwischen den Himmelskörpern berechnen kann.
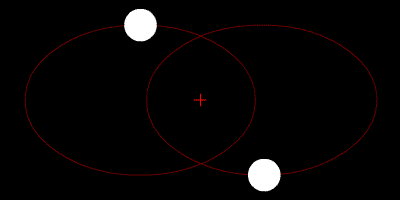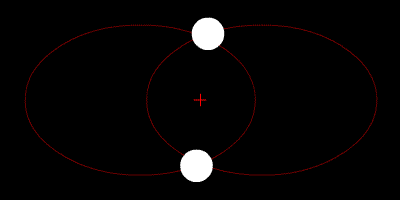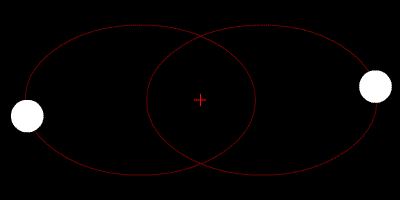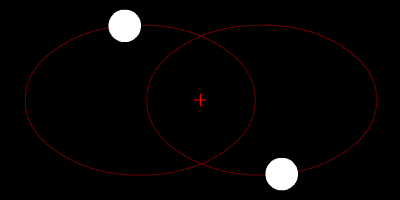
Simpel: Das Zweikörperproblem (Bild: Public Domain)
Dass, was Kepler untersucht hatte, entspricht aus heutiger Sicht einem Zweikörperproblem. Er gab Regeln an, die beschreiben wie sich ein Planet um einen Stern herum bewegt. Diese Regeln gewann er aus der Interpretation von Beobachtungsdaten – mit Newtons Formel für die Wirkung der Gravitation ließ sich dieses Problem später dann auch mathematisch behandeln. Stellt man die entsprechenden Gleichungen auf die beschreiben, wie die Gravitation zwischen Stern und Planet wirkt und löst diese, dann erhält man genau das gleiche Ergebnis, auf das auch schon Kepler gekommen ist. Alle Planeten bewegen sich entlang elliptischer Bahnen um die Sonne (Keplers 1. Gesetz), sie bewegen sich umso schneller, je näher sie auf ihrer Bahn der Sonne kommen (Keplers 2. Gesetz) und eine Umrundung der Sonne dauert umso länger, je größer die Bahn ist (Keplers 3. Gesetz).
Es war aber schon damals klar, dass diese Lösung nicht die echte Lösung sein konnte. Denn unser Sonnensystem besteht nicht nur aus einem Planet und einem Stern. Und jeder Himmelskörper übt eine gravitative Wirkung auf jeden anderen Himmelskörper aus. In Keplers Beschreibung des Sonnensystem bewegt sich aber jeder Planet völlig unabhängig und ungestört von allen anderen Planeten. Mit Newtons Gleichungen wäre es nun aber theoretisch möglich, all diese Wechselwirkungen zu berechnen und ein reales Bild der Bewegung der Planeten zu erhalten.
Es gelang allerdings niemand, diese Gleichungen auch tatsächlich zu lösen. Die größten Mathematiker der letzten Jahrhunderte haben sich daran versucht und blieben erfolglos. Nicht einmal der scheinbar leichte Fall der Bewegung dreier Himmelskörper konnte gelöst werden und das verschafft dem Dreikörperproblem die Faszination, die ihm bis heute innewohnt.
Das Dreikörperproblem lässt sich leicht formulieren: Wie bewegen sich drei Himmelskörper unter ihrer gegenseitigen gravitativen Anziehungskraft? Bei nur zwei Körper ist es einfach. Kenne ich Position und Geschwindigkeit der beiden Objekte zu einem bestimmten Zeitpunkt, dann kann ich Newtons Formel benutzen, um ihre Position und Geschwindigkeit für jeden beliebigen Zeitpunkt in der Zukunft zu berechnen (und diese Lösung ist identisch mit dem, was qualitativ durch Keplers Gesetze beschrieben wird). Aber sobald ein dritter Körper dazu kam, wurde das Problem viel, viel schwerer zu lösen.
Also verlegten sich die Astronomen und Mathematiker vorerst darauf, Fälle zu untersuchen die ein bisschen einfacher waren. Dazu gehört das sogenannte eingeschränkte Dreikörperproblem. Auch hier wird die Bewegung dreier Himmelskörper betrachtet. Um die Sache ein bisschen weniger kompliziert zu machen, geht man aber davon aus, dass eines der drei Objekt viel weniger Masse hat als die anderen beiden, so dass man seine gravitative Wirkung vernachlässigen kann. Man hat dann zwei Himmelskörper, die sowohl einander als auch den kleinen dritten Körper beeinflussen und eben diesen dritten Körper, der nur beeinflusst wird, selbst aber keine gravitative Wirkung auf die anderen beiden ausübt.Ein gutes Beispiel dafür ist die Bewegung eines Asteroiden oder kleinen Mondes in der Nähe eines großen Planeten: Sonne und Planet beeinflussen die Bewegung des Asteroiden und Sonne und Planet beeinflussen natürlich auch ihre gegenseitige Bewegung. Aber der winzige Asteroid hat viel zu wenig Masse, um irgendeine relevante Wirkung auf Sonne oder Planet auszuüben.
Aber auch das eingeschränkte Dreikörperproblem erwies sich als schwer zu lösen. Immerhin aber gelang es hier, bestimmte Spezialfälle zu identifizieren, über die sich dann doch etwas aussagen ließ. Dazu gehören die berühmten Lagrange-Punkt (die vom französischen Mathematiker Joseph Louis-Lagrange im 18. Jahrhundert gefunden wurden). Im eingeschränkten Dreikörperproblem gibt es fünf ganz spezielle Punkte, an denen sich alle wirkenden Kräfte der beiden großen Körper exakt aufheben. Der dritte kleine Körper kann sich dort für lange Zeit auf stabilen und vorhersagbaren Bahnen bewegen. Das eingeschränkte Dreikörperproblem ist zwar immer noch ein vereinfachtes Modell, aber immerhin gut genug, um auch in der Realität Anwendung zu finden. Denn betrachtet man zum Beispiel die Lagrange-Punkte der Planeten in unserem Sonnensystem, dann findet man in ihrer Nähe tatsächlich viele kleine Himmelskörper: Die “Trojaner”-Asteroiden, über die ich hier und hier mehr geschrieben habe (sogar unsere Erde hat ihren eigenen Trojaner).
Die Lagrange-Punkte sind stationäre Lösungen für das Dreikörperproblem. Ein Objekt, das sich exakt in einem Lagrange-Punkt befindet, wird auch für alle Zeiten genau dort bleiben (Aber natürlich bewegt sich der Lagrange-Punkt immer noch um die Sonne herum, da seine Position ja von der Position des sich ebenfalls bewegenden Planeten abhängt. Das “stationär” bezieht sich auf die Lösung, also die Bahn des Himmelskörpers, die sich nicht verändert, nicht auf seine Position). Das ist noch weit von einer allgemeinen Lösung entfernt, aber es war zumindest ein Anfang. 1911 fand der amerikanische Astronom William Duncan MacMillan dann einen weiteren Spezialfall, der heute meistens unter dem Namen des russischen Mathematikers Kirill Alexandrowitsch Sitnikow bekannt ist,der es in den 1960er Jahren weiter bearbeitet hat. Das Sitnikov-Problem basiert ebenfalls auf dem eingeschränkten Dreikörperproblem: Zwei (annähernd gleich) große Himmelskörper umkreisen einander unter ihrem gegenseitigen gravitativen Einfluss. Der kleine, dritte Himmelskörper befindet sich genau im Massenschwerpunkt der beiden großen und wenn das der Fall ist, dann – so fanden MacMillan und Sitnikov heraus – führt er nur eine eindimensionale Bewegung aus. Das soll heißen: Der dritte Himmelskörper bewegt sich ausschließlich entlang einer Linie, die durch den Massenschwerpunkt führt und senkrecht auf die Ebene steht, in der sich die beiden großen Objekte bewegen. Hier ist ein Video, dass zeigt wie das aussehen kann:
Auch für das Sitnikov-Problem existiert keine allgemeine exakte Lösung, die die Bewegung der Himmelskörper für alle Zeiten vorhersagen kann. Aber MacMillan und Sitnikov konnten zumindest für einige spezielle Konfigurationen periodische Lösungen identifizieren. Für andere Fälle ist die Bewegung des dritten Körpers aber extrem unvorhersagbar und chaotisch, wie ich hier ausführlich erklärt habe.
Und was das allgemeine Dreikörperproblem anging, war man auch noch nicht wirklich weitergekommen. Ganz im Gegenteil: Gegen Ende des 19. Jahrhunderts zeigte der französische Mathematiker Henri Poincaré, dass es unmöglich ist, das Dreikörperproblem zu lösen. Genauer gesagt konnte er nachweisen, dass man niemals eine einfache mathematische Gleichung finden kann, mit der sich Position und Geschwindigkeit dreier beliebiger Himmelskörper für alle Zeiten vorhersagen lassen. Eigentlich war Poincaré zuerst überzeugt, er hätte das Dreikörperproblem gelöst und stellte erst später fest, dass er sich geirrt hatte. Dafür aber legte er mit seiner korrigierten Version gleich auch den Grundstein für die moderne Chaostheorie! (Ich habe die Geschichte von Poincarés Entdeckung ausführlicher in meinem aktuellen Buch “Asteroid Now: Warum die Zukunft der Menschheit in den Sternen liegt”* beschrieben)
Es gibt (unter anderem) zwei wichtige Gründe, die das Dreikörperproblem so schwer zu lösen machen. Über einen davon habe ich in meiner Artikelserie über Störungsrechnung (Teil 1, Teil 2, Teil 3, Teil 4) geschrieben: Wenn die Umlaufzeiten zweier Himmelskörper in einem ganzzahligen Verhältnis zueinander stehen, können sich die gravitativen Wirkungen im Laufe der Zeit aufschaukeln und so eine Resonanz (siehe hier für Details) macht die Bewegung unvorhersagbar und die mathematische Behandlung so gut wie unmöglich. Der zweite wichtige Punkt sind Kollisionen: Wenn zwei Himmelskörper miteinander zusammenstoßen, dann befinden sie sich zur gleichen Zeit am gleichen Ort und der Abstand zwischen ihnen wird dabei Null. Der Abstand bestimmt aber, wie groß die gravitative Wirkung ist und spielt eine fundamentale Rolle in den Formeln die zur Berechnung der Bewegung nötig sind. Je kleiner der Abstand, desto größer die Gravitationskraft. Und wenn der Abstand verschwindet, dann wird die Gravitationskraft unendlich groß!

Kollisionen machen auch das Dreikörperproblem kaputt! (Bild: NASA/JPL/Caltech)
Mit unendlich großen Zahlen und einer Division durch Null kommt die Himmelsmechanik nicht wirklich gut klar und es ist kein Wunder, dass das Dreikörperproblem unlösbar blieb. Denn wie sollte man ausschließen, dass es niemals zu Kollisionen kommen kann? Ganz einfach: In dem man es einfach ausschließt! Das war zumindest das, was der finnische Mathematiker Karl Frithiof Sundman im Jahr 1912 gemacht hat. Er war der erste, der eine Lösung für das Dreikörperproblem angeben konnte. Allerdings nicht in Form einer einfachen Gleichung (dass das nicht geht hatte ja Poincaré schon gezeigt), sondern in Form einer unendlich langen mathematischen Reihe. Das klingt seltsam, ist es aber nicht: Ein Beispiel: Die Summe 1 + 1/2 + 1/4 + 1/8 + 1/16 + … hat unendlich viele Einträge. Trotzdem ist das Ergebnis nicht unendlich groß sondern einfach gleich 2. Jeder neue Eintrag in der Summe ist ausreichend kleiner als der vorherige und damit ist sicher gestellt, dass die gesamte Summe niemals beliebig groß werden kann. Man nennt das eine konvergente Reihe und genau so sah die Lösung aus, die Sundman für das Dreikörperproblem gefunden hatte. Damit er zu dieser Lösung kommen konnte, musste er allerdings vorab fordern, dass es niemals zu einer Kollision der drei Himmelskörper kommen kann (vereinfacht gesagt; wer alle Details zu Sundmans Geschichte erfahren will, dem empfehle ich diesen ausführlichen wissenschaftshistorischen Artikel (pdf)). Abgesehen davon war Sundmans Lösung zwar durchaus beeindruckend, aber leider auch völlig unbrauchbar. Denn um mit der unendlichen Summe die Lösung des Dreikörperproblems so genau zu berechnen, dass man damit brauchbare astronomische Vorhersagen treffen kann, müsste man sehr, sehr viele der unendlich vielen Einträge der Reihe berechnen. Die Zahl der nötigen Terme ist in diesem Fall wirklich absurd groß: Es wäre eine 1, auf die 8 Millionen Nullen folgen! Vereinfacht gesagt: Sundmans Lösung existiert zwar, ist aber in der Praxis vollkommen unbrauchbar um damit irgendetwas anzustellen.
Das Dreikörperproblem hat die Astronomen aber trotzdem weiter beschäftigt und tut das weiterhin. 1993 entdeckte der amerikanische Physiker Christopher Moore eine weitere periodische Lösung und zwar eine wirklich faszinierende. In seiner Arbeit (“Braids in classical dynamics”, pdf) konnte er zeigen, dass sich drei Himmelskörper unter bestimmten Voraussetzungen hintereinander entlang einer Bahn bewegen können, die die Form einer “8” hat. Wie drei Autos auf einer Rennstrecke sausen sie die 8 entlang und tun das für alle Zeiten und auf exakt vorhersagbare Weise. Diese periodische Lösung ist aber, so wie auch die des Sitinikov-Problems, nur von mathematischen Interesse. Es ist kaum vorstellbar, dass sich so spezielle Konfigurationen wie die von Sitnikov oder Moore irgendwo im realen Universum tatsächlich finden sollten.
Aber wer weiß, was aus diesen mathematischen Spezialfällen irgendwann für neue Erkenntnisse erwachsen! Deswegen ist es auch gut, wenn sich die Wissenschaftler weiterhin Gedanken darüber machen. Erst vor kurzem ist den Serben Milovan Šuvakov und Veljko Dmitrašinović dabei ein regelrechter Durchbruch gelungen. Sie fügten den bisher bekannten stationären/periodischen Lösungen gleich 13 (!) neue Fälle hinzu (“Three Classes of Newtonian Three-Body Planar Periodic Orbits”). Manche dieser Lösungen sind sehr simpel, andere sind höchst komplex. Sie tragen Namen wie “Bumblebee”, “Yin-Yang” oder “Dragonfly” und man kann sie hier betrachten. Das hier zum Beispiel ist die “Motte” (und bei weitem nicht das komplexeste Bewegungsmuster der drei Himmelskörper, das sich in der serbischen Sammlung findet):
Das Dreikörperproblem wird die Astronomen und Mathematiker mit Sicherheit auch in der Zukunft beschäftigen. Eine einfach Lösung, mit der sich für alle Fälle die Bewegung der Himmelskörper für jeden beliebigen Zeitpunkt vorhersagen lässt, wird es allerdings nicht geben. Aber das ist zumindest in der Praxis auch nicht nötig. Mittlerweile haben wir ja Computer, die sehr schnell sehr viele Rechnungen durchführen können. Damit ist es heute sehr einfach, die Gleichungen, die rein mathematisch nicht vollständig lösbar sind, am Computer numerisch und näherungsweise zu lösen. Diese “Näherungslösungen” sind aber so exakt, dass wir dank ihnen zum Beispiel Raumsonden punktgenau durchs Sonnensystem steuern können. Was die konkrete Astronomie angeht, stellt das Dreikörperproblem also schon längst kein Problem mehr dar. Aber trotzdem: Die Komplexität die hinter der Bewegung dreier Himmelskörper steckt und die Unmöglichkeit einer vollständigen Beschreibung werden die Mathematiker weiterhin faszinieren. Und wer weiß, welche speziellen Lösungen man hier doch noch finden kann…













Kommentare (48)