Wie werden Wahrscheinlichkeiten im Alltag wahrgenommen – und welche Probleme ergeben sich daraus? Und was um alles in der Welt haben flüchtende Taxifahrer mit spanischen Bombenlegern zu tun?
Das Taxi-Problem gehört zu den Themen, die ich in meinen Vorlesungen immer wieder sehr gerne behandle. Noch unterhaltsamer ist eigentlich nur noch das Ziegen-Problem, zu dem ja Jürgen in GeoGraffitico vor einiger Zeit schon mal etwas geschrieben hatte.
Grüne und blaue Taxen…
Die Ausgangssituation des Taxi-Problems sieht wie folgt aus: In einer nicht näher bezeichneten Stadt existieren zwei konkurrierende Taxi-Unternehmen. Die Taxen des ersten Unternehmens, „Green Cab”, sind grün, die Taxen des zweiten Unternehmens, „Blue Cab”, dagegen blau. Der Marktanteil von „Green Cab” liegt bei 85%, womit (da ja kein drittes Unternehmen existiert) 15% Marktanteil für „Blue Cab” verbleiben.
Nun kommt es zu einem Verkehrsunfall mit Fahrerflucht, für den es leider nur einen einzigen Zeugen gibt. Dieser Zeuge gibt an, der Fahrer eines blauen Taxis habe den Unfall verursacht, und sei anschließend mit dem Fahrzeug geflohen. Andere Spuren gibt es nicht, so dass die ermittelnde Behörde sich auf die Aussagen des Zeugen verlassen muss. Der antwortet zwar ehrlich und nach bestem Wissen und Gewissen – aber wie groß ist die Wahrscheinlichkeit, dass seine Schilderung des Unfallhergangs trotzdem fehlerhaft ist?
Dass er ein Taxi gesehen hat, steht außer Frage, da sich auf allen Taxen in unserer Stadt die Aufschrift „TAXI” in riesigen Lettern findet. Da der Zeuge sich in diesem Punkt also kaum irren kann und zudem keinen Grund für eine Falschaussage hat, arbeitet der flüchtige Fahrer also mit Sicherheit für eines der beiden Taxi-Unternehmen. Aber was ist mit der Farbe des Wagens? Der Zeuge ist sich zwar sicher, ein blaues Taxi erkannt zu haben, könnte sich aber auch irren, denn immerhin war es schon ziemlich dämmrig…
Die ermittelnde Behörde führt daher einen Test mit dem Zeugen durch, in dessen Rahmen er Farbbeispiele vorgeführt bekommt, an die er sich später erinnern soll. Zur Freude der Ermittler zeigt sich, dass der Zeuge über ein sehr gutes Farbgedächtnis verfügt, denn es gelingt ihm, 80% der Farbbeispiele richtig zuzuordnen. Lässt sich daraus nun der Schluss ziehen, dass auch die Beschreibung des Unfallwagens mit 80%iger Sicherheit korrekt ist?
Warum ist diese Annahme falsch?
Die meisten Menschen würden dieser Aussage wohl auf Anhieb zustimmen – mir ging es jedenfalls so. Und es klingt doch auch logisch: Wenn der Zeuge einen Wagen mit x-beliebiger Farbe sieht, dann liegt die Wahrscheinlichkeit dafür, dass er sich später korrekt an die Farbe erinnern kann, genau bei 80%. Demnach müsste das Unfalltaxi doch ebenfalls mit 80%iger Wahrscheinlichkeit blau gewesen sein?
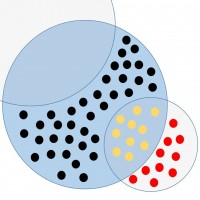
Tatsächlich ist dem aber nicht so, denn man vernachlässigt bei der Schlussfolgerung die Tatsache, dass in der Stadt sehr viel mehr grüne als blaue Taxen unterwegs sind. Nehmen wir einfach mal an, in der Stadt sind insgesamt nur 100 Taxen unterwegs (es ist eine sehr kleine Stadt). Von diesen 100 Taxen muss eines in den Unfall verwickelt gewesen sein – und aus den jeweiligen Marktanteilen von 85% bzw. 15% ergibt sich, dass 85 grüne und 15 blaue Taxen die Straßen der Stadt „bevölkern”.
Wie wir wissen, ist sich der Zeuge sicher, ein blaues Taxi gesehen zu haben. Dass er mit 80%iger Wahrscheinlichkeit richtig liegt bedeutet natürlich auch, dass er in 20% aller Fälle die Farbe nicht korrekt zuordnen kann. Er würde demnach von den 85 grünen Taxen 68 korrekt als grün erkennen und 17 fälschlicherweise als blau. Umgekehrt würde er von den 15 blauen Taxen 12 korrekt als blau erkennen und 3 fälschlicherweise als grün. Diese Umstände gilt es bei der die Berechnung der Wahrscheinlichkeit für ein blaues Unfalltaxi zu beachten.
Letztendlich gibt es vier Möglichkeiten, wie die Geschichte ablaufen kann:
- Das Unfalltaxi war grün und wird als grün erkannt
- Das Unfalltaxi war grün und wird als blau erkannt
- Das Unfalltaxi war blau und wird als blau erkannt
- Das Unfalltaxi war blau und wird als grün erkannt
Oder (ad hoc und unschön) grafisch dargestellt:
Da die Zeugenaussage (blaues Taxi) bereits vorliegt, interessieren uns zwei der vier Ereignisketten nicht weiter. Konzentrieren wir uns also auf die beiden anderen:
- Das Unfalltaxi war grün und wird als blau erkannt
- Das Unfalltaxi war blau und wird als blau erkannt
Wie man sieht, besteht jede Ereigniskette aus zwei Einzelereignissen, nämlich
- Taxi der Farbe xy ist in den Unfall verwickelt und
- Farbe xy des Taxis wird richtig / falsch erkannt
Die Wahrscheinlichkeit für das richtige Erkennen der Farbe ist uns aus dem Test bekannt, sie liegt bei 80%. Die Wahrscheinlichkeit des vorausgehenden Ereignisses („Taxi der Farbe xy ist in den Unfall verwickelt”) ergibt sich aus den Marktanteilen der beiden Taxi-Unternehmen. Wenn man nun noch beachtet, dass die Irrtumswahrscheinlichkeit des Zeugen bei 20% liegt (wenn er in 80% aller Fälle die Farbe richtig erkennt), dann kann man den beiden verbleibenden Ereignisketten leicht die Wahrscheinlichkeiten zuordnen:
- Das Unfalltaxi war grün (85%) und wird als blau erkannt (20%)
- Das Unfalltaxi war blau (15%) und wird als blau erkannt (80%)
Wie groß ist nun die Wahrscheinlichkeit dafür, dass das Unfalltaxi tatsächlich blau gewesen ist, wie der Zeuge behauptet? In der Statistik verwenden wir für Berechnungen mit so genannten “bedingten Wahrscheinlichkeiten” den Satz von Bayes. Dabei wird die Wahrscheinlichkeit des zu untersuchenden Ereignisses (blaues Taxi wird als blau erkannt) ins Verhältnis zur Summe der bedingten Wahrscheinlichkeiten aller Ereignisketten gesetzt (blaues Taxi wird als blau erkannt und grünes Taxi wird als blau erkannt):
Wir landen bei einer Wahrscheinlichkeit von gerade mal 41%! Ein verblüffendes Ergebnis – obwohl der Zeuge eine 80%ige Sicherheit bei der Identifikation von Farben an den Tag legt, liegt die Wahrscheinlichkeit dafür, dass das Taxi tatsächlich blau gewesen ist, unterhalb der 50%-Grenze. Was nichts anderes bedeutet, als dass man bessere Chancen hat, die Farbe des Unfalltaxis zu ermitteln, wenn man einfach eine Münze wirft…
Aber ist das Ganze nun eine mathematische Spielerei, oder ein praxisrelevantes Problem?
Auch wenn es auf den ersten Blick wie eine Spielerei erscheint, ist das dargestellte Problem sogar im höchsten Maße praxisrelevant – unter anderem natürlich auch für „echte” Ermittlungen oder Gerichtsverfahren, in denen Zeugenaussagen eine Rolle spielen. Es begegnet uns aber auch anderswo – nämlich überall dort, wo bedingte Wahrscheinlichkeiten nicht richtig wahrgenommen werden. Wie im Falle des Taxi-Problems wird viel zu häufig eine Wahrscheinlichkeit (der Zeuge liegt in 80% aller Fälle richtig) korrekt interpretiert, eine andere (nur 15% aller Taxen sind blau) jedoch einfach „ausgeblendet”.
Wo tritt so etwas noch auf?
Beispielsweise bei flächendeckenden HIV-Tests. Die gibt es nämlich aus gutem Grund nicht. Zwar sind die Tests an sich sehr ergebnissicher (mehr noch als der Zeuge im Taxi-Fall), der Anteil der HIV-Infizierten in der Bevölkerung ist jedoch – dem Himmel sei Dank – äußerst gering (sehr viel geringer als der Anteil der blauen Taxen). Ein flächendeckender Test würde zu einer so großen Menge an Fehldiagnosen führen, dass er einfach keinen Sinn macht – trotz der hohen Güte des eigentlichen Testverfahrens.
Auch in der Terror-Abwehr spielen bedingte Wahrscheinlichkeiten eine große Rolle. Ein Beispiel mit Fehlalarmen in spanischen Hotels habe ich vor Jahren mal mit meinen Studenten berechnet. In diesem Szenario gab es einen Terrorismus-Experten, der sogar mit 95%iger Sicherheit eine echte von einer falschen Bombendrohung unterscheiden konnte – eine wesentlich bessere „Trefferquote” als unser Zeuge im Taxi-Fall. Trotzdem veranlasst dieser Experte eine überflüssige Hotel-Evakuierung nach der anderen.
Warum? Natürlich deshalb, weil in unserem Szenario (wie auch im wahren Leben) auf einen „echten” ETA-Terroristen knapp hundert Idioten kommen, die eine Bombendrohung nur so zum Spaß durchgeben. Echte Drohungen und „Spaßdrohungen” stehen also in einem sehr viel krasseren Mißverhältnis zueinander, als grüne und blaue Taxen – und das führt dann auch bei einer Sicherheit von 95% zu so vielen „false positives”, dass es auf Außenstehende fast wie ein Ratespiel des Experten wirkt.
Nicht richtig wahrgenommene bedingte Wahrscheinlichkeiten finden wir im Alltag sozusagen „an jeder Ecke”. Es gäbe etliche weitere gute Beispiele – da ich den Post aber nicht in extreme Längen ziehen möchte, belasse ich es an dieser Stelle mal bei einigen Nennungen. Wer sich für die Thematik begeistern kann, kann sich ja am Wochenende spaßeshalber mal darüber Gedanken machen, welchen Zusammenhang es zwischen diesen Stichwörtern und dem Problem der falschen Wahrnehmung von bedingten Wahrscheinlichkeiten geben könnte:
- „Cold Reading”
- Ausländerkriminalität
- Horoskop-Vorhersagen
- DNA-Tests vor Gericht
- BSE-Massentests bei Kühen
- Gewalttätige Computerspieler
- „Homeland Alert Level” in den USA
Jedem, der es versucht, wünsche ich jetzt schon ein vergnügliches Wochenende. Falls daran Interesse bestehen sollte, kann ich das eine oder andere Szenario gerne mal ausführlich und mit Zahlenbeispielen hier im Blog „durchkauen”. Das Kommentarfeld wartet auf Eingaben…
Lesetipp: Mark Daniel Schweizer: Kognitive Täuschungen vor Gericht – eine empirische Studie, Dissertation an der Rechtswissenschaftlichen Fakultät Zürich, 2005


Kommentare (24)