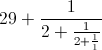
Das Prinzip sollte mittlerweile klar sein, oder? Als nächstes käme dann
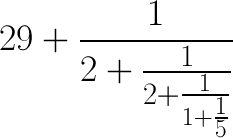
Und so kann man das Spiel immer weiter spielen. Der entstehende Kettenbruch wird die ursprüngliche Zahl immer genauer approximieren. Aber für uns reicht es erstmal. So einen Kettenbruch kann man natürlich auch wieder in einen normalen Bruch umrechnen. Unsere erste Approximation war 29 + 1/2. Umgerechnet ergibt das 59/2. Die nächste Approximation war 29 + 1/(2+1/2), was dem Bruch 147/5 entspricht. Der nächste verbesserte Kettenbruch liefert 206/7 und der letzte Kettenbruch, bei dem wir dann gestoppt haben, vereinfacht sich zu 1177/40. Dank der Methode mit den Kettenbrüchen haben wir also einen einfachen Weg, um eine Reihe von Brüchen zu finden, die unsere Ausgangszahl immer besser approximieren!
Christiaan Huygens hatte damals bei 206/7 halt gemacht. Dieser Bruch näherte das Verhältnis der Umlaufzeiten von Saturn und Erde ausreichend gut an. Das Zahnrad für den Saturn brauchte also 206 Zähne, das für die Erde nur 7 – dann würden sie sich ausreichend genau mit der richtigen Geschwindigkeit bewegen!
Aber was hat das alles mit dem goldenen Schnitt zu tun? Der “goldene Schnitt” ist das berühmte Teilungsverhältnis, dass man überall in der Kunst und der Natur findet. Man teilt dabei eine Strecke so, dass das Verhältnis der Gesamtstrecke zum größeren Abschnitt dem Verhältnis des größeren zum kleineren Abschnitt entspricht. Nennt man diese beiden Abschnitte a und b, dann kann mit ein wenig Geometrie (ich zeig das jetzt nicht vor) leicht ausrechnen, dass das Verhältnis a/b immer einen bestimmten Wert haben muss. Diese Zahl nennt man Φ, die Zahl des goldenen Schnitts:
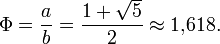
Diese Zahl ist irrational, sie lässt sich also nicht als Bruch mit zwei ganzen Zahlen schreiben. Aber natürlich kann man mit ihr das gleiche Spiel spielen, wie Huygens mit seinem Verhältnis von Planetenumläufen. Tut man das, dann bekommt man einen äußerst interessanten Kettenbruch:
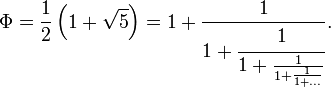
Er besteht nur aus Einsen! Was bedeutet das? Erinnern wir uns an die Art und Weise, wie man den Kettenbruch konstruiert: Man bestimmt einen Näherungsbruch, und berechnet den Fehler. Dieser Fehler wird dann wieder in einen Näherungsbruch umgewandelt, der an den ursprünglichen Bruch dran gehängt wird. Dann berechnet man den Fehler davon, und so weiter. Wichtig ist, dass der Fehler immer unter dem Bruchstrich steht. Ist der Fehler klein, dann muss die Zahl unter dem Bruchstrich groß sein (1/10 ist ein wesentlich kleinerer Fehler als 1/2). Ist der Fehler groß, dann ist die Zahl klein. Wenn also in der Kettenbruchentwicklung von Φ nur Einsen, also nur kleine Zahlen vorkommen, dann heißt das, dass wir bei jedem Schritt der Approximation einen großen Fehler machen. Schlechter geht es in diesem Fall nicht mehr. Die Zahl des goldenen Schnitts ist von allen irrationalen Zahlen diejenige, die sich am schlechtesten durch einen Bruch nähern lässt!
Das ist übrigens auch der Grund, warum sie in der Natur so oft zu finden ist. Da ist es nämlich oft von Vorteil, wenn bestimmte Dinge, wie zum Beispiel die Anordnung von Blättern oder Blütenständen bei Pflanzen, möglichst schlecht approximierbar sind. Ein Blättermuster, dass sich schnell exakt wiederholt, also mit einer Periode die durch einen kleinen Bruch approximierbar ist, führt z.B. dazu, dass die Blätter direkt übereinander stehen und sich gegenseitig das Licht wegnehmen (ich habe das hier genauer erklärt).
Mit dem goldenen Schnitt lässt sich aber auch noch jede Menge anderes cooles Zeug anstellen. Sie eignet sich offensichtlich ideal, um daraus ein Metal-Lied zu machen. Im “Golden Ratio Song” wird nicht nur über den goldenen Schnitt gesungen, auch die Musik selbst wird durch Φ bestimmt. Das Ergebnis ist genial:
Im “Making of” des Videos wird nochmal ausführlich erklärt, wo der goldene Schnitt überall auftaucht:











Kommentare (16)