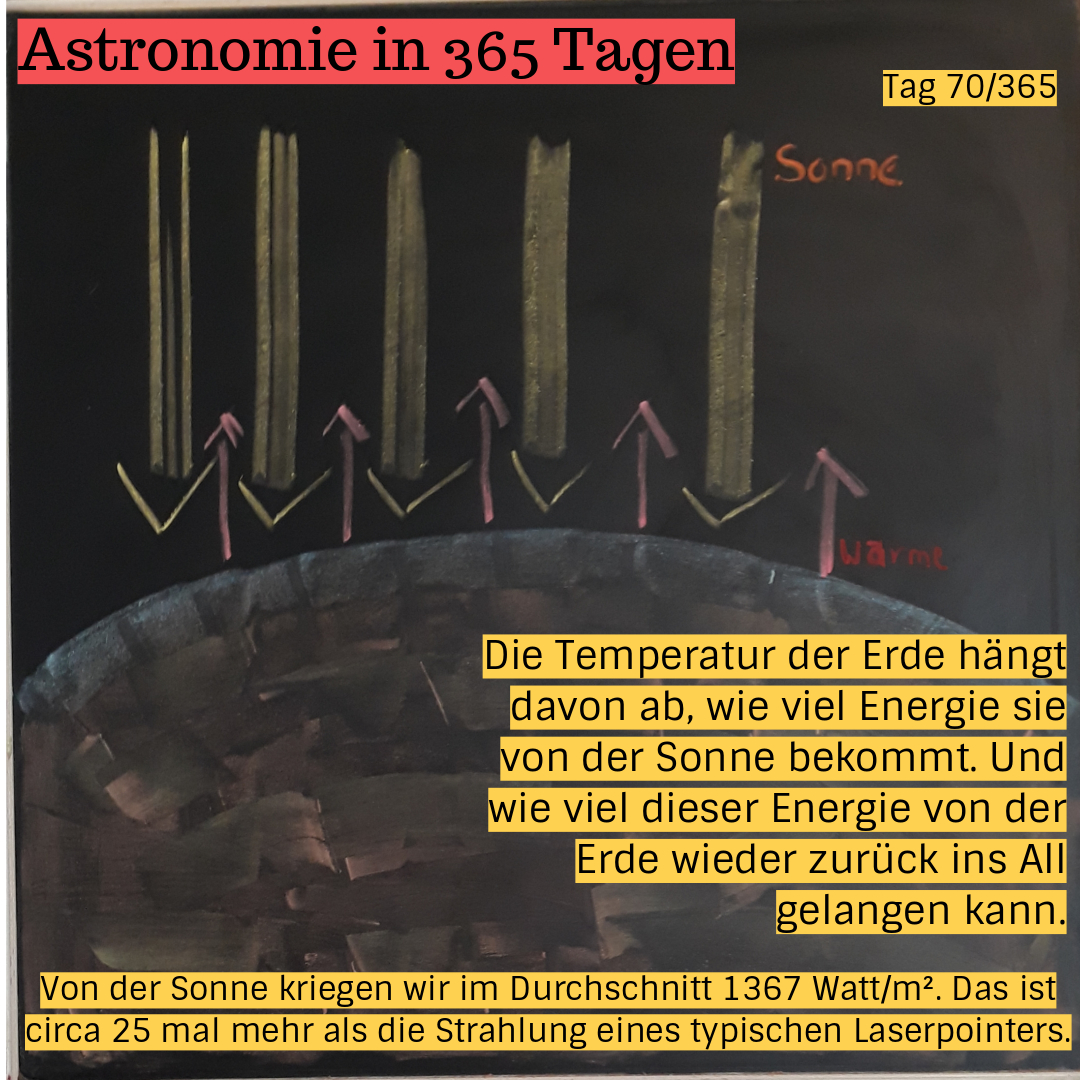
Die Temperatur der Erde hängt davon ab, wie viel Energie sie von der Sonne bekommt. Und wie viel dieser Energie von der Erde wieder zurück ins All gelangen kann. Von der Sonne kriegen wir im Durchschnitt 1367 Watt/m². Das ist circa 25 mal mehr als die Strahlung eines typischen Laserpointers.
—————————–
Das hier ist die Blog-Seite zur Einführung in die Astronomie “Astronomie in 365 Tagen” bei Instagram. An jedem Tag des Jahres gibt es eine neue Lektion; Details zum Projekt gibt es hier. Wer möchte, kann über meinen Instagram-Account bzw #astronomie365 mit dabei sein.
Ich hab die Domain astronomie365.de eingerichtet unter der die gesammelten Blogartikel erreichbar und leichter verlinkbar sind.
Falls jemand Lust hast, sich grafisch besser auszutoben als ich und die Bilder für andere Zwecke anders formatieren will findet man die Rohdaten der Bilder hier bei Google Drive. Die Texte dazu gibt es bei den jeweiligen Blogartikeln (Solange ich als Autor genannt und die Texte nicht verändert werden, können diese Bilder gerne weiterverwendet werden).
Text Tag 70
Tag 70/365: Die Temperatur der Erde hängt davon ab, wie viel Energie sie von der Sonne bekommt. Und wie viel dieser Energie von der Erde wieder zurück ins All gelangen kann. Von der Sonne kriegen wir im Durchschnitt 1367 Watt/m². Das ist circa 25 mal mehr als die Strahlung eines typischen Laserpointers.











Kommentare (18)