Es herrscht immer noch Covid-19-Pandemie und Corona-Krise. Und ich bin immer noch nur Astronom und kein Virologe. Weswegen ich die Interpretation des Geschehens und die medizinischen Ratschläger weiterhin den echten Expertinnen und Experten überlasse. Was aber nichts daran ändert, dass mich das Thema – natürlich! – sehr interessiert. Unter anderem die Frage die derzeit vermutlich alle beschäftigt: Wie lange wird dieser Ausnahmezustand noch dauern? Wann wird alles wieder “normal”? Das interessiert mich einerseits ganz persönlich: Ein großer Teil der Arbeit mit der ich meinen Lebensunterhalt verdiene findet derzeit nicht statt und auch wenn es mir glücklicherweise besser geht als denen deren Geschäfte und Tätigkeiten momentan komplett ruhen und die überhaupt kein Einkommen haben. So wie alle anderen will ich auch wieder in Urlaub fahren, Freunde und Familie treffen, ins Restaurant gehen, und so weiter. Mich interessiert die Frage aber auch, weil sie etwas berührt mit dem ich als Wissenschaftler tatsächlich viel zu tun hatte: Computersimulationen!
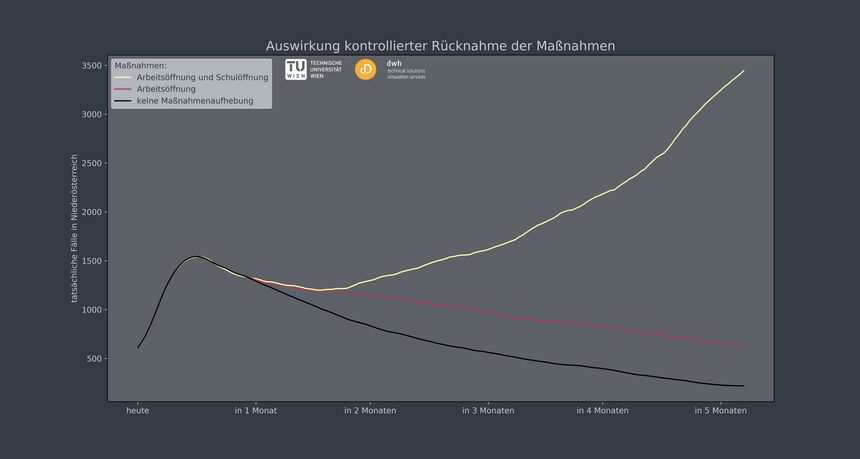
In den Medien sehen wir derzeit immer wieder Diagramme wie dieses hier:
Es stammt von Computersimulationen die von der TU Wien durchgeführt werden und zeigt wie sich die Situation in Österreich (ähnliche Diagramme wird es vermutlich auch für Deutschland und andere Länder geben) entwickeln könnte. Die schwarze Kurve zeigt – für das Beispiel des Bundeslandes Niederösterreich – die Entwicklung der Covid-19-Fälle im Laufe der Zeit. Es werden vorerst immer mehr Menschen infiziert, dann irgendwann weniger und irgendwann im August ist alles mehr oder weniger vorbei. Allerdings nur unter der Bedingung dass sämtliche Maßnahmen die jetzt existieren (Ausgangsbeschränkungen, Schulschließungen, usw) auch weiterhin in Kraft bleiben. Was eher düstere Aussichten sind – es ist zweifelhaft ob wir das bis zum Sommer durchhalten. Die rote Kurve zeigt was passiert, wenn wir die Leute nach Ostern zumindest wieder arbeiten gehen lassen. Dann wird es etwas länger dauern bis die Zahl der infizierten Menschen sinkt aber nicht dramatisch viel länger. Sollten wir nach Ostern aber auch die Schulen öffnen, wird die Lage sich dramatisch ändern. Dann werden die Fälle steigen und im Sommer ist alles sehr viel schlimmer als jetzt.
Solche Diagramme sind nicht nur interessant. Sondern natürlich auch eine wichtige Handlungsgrundlage für die Politik. Aber, und das ist die Frage die ich mir in den letzten Tagen gestellt habe: Wie berechnet man so etwas eigentlich? Ich kenne mich mit Computersimulationen aus, die das Universum betreffen. Wenn jemand wissen möchte, wie sich Planeten oder Asteroiden in den nächsten Jahrhunderttausenden bewegen: Kein Problem! Genau so etwas zu modellieren und zu berechnen war mein Job in meiner Zeit als Wissenschaftler. Aber Menschen sind keine Himmelskörper und Viren ebenfalls nicht. Wie modelliert man die und wie findet man heraus, welchen Effekt die Schließung von Schulen oder Arbeitsstätten auf die Ausbreitung einer Krankheit hat?
Ich habe also ein wenig recherchiert (ohne Anspruch auf Vollständigkeit!) um herauszufinden, wie sehr sich die epidemiologischen Computersimulationen von denen der Himmelsmechanik unterscheiden. Die kurze Antwort: Sehr! Die etwas längere Antwort: Sehr, aber zumindest was die Grundlagen angeht, gibt es Ähnlichkeiten.
Die mathematische Behandlung des ganzen Themenkomplexes kann man grob in zwei Bereiche aufteilen. Da ist zuerst einmal die Frage nach der Ausbreitung der Krankheit in einer Gruppe von Menschen. Wenn man es ganz simpel betrachtet gibt es gesunde Menschen die sich infizieren können und infizierte Mensche die Gesunde anstecken können. So ein Modell nennt man SI-Modell (von “S” für “susceptible”, also die gesunden Menschen und “I” für die Infizierten). Die Wechselwirkung zwischen beiden Gruppen lässt sich dann durch eine relativ simple Differentialgleichung beschreiben. Die Menge der Gesunden wird immer kleiner und gleichzeitig muss die Gruppe der Infizierten um die gleiche Anzahl wachsen. Wie schnell das passiert (am Ende sind in diesem Modell alle infiziert), hängt von der Ausbreitungsgeschwindigkeit der Krankheit ab. So ein Modell ist natürlich nicht wahnsinnig realistisch, denn zum Glück werden infizierte Menschen ja auch immer wieder mal gesund. Deswegen gibt es auch “SIR-Modelle”, wo noch die Gruppe der “removed individuals” dazu kommt, also derjenigen, die aus der ganzen Krankheitssache raus sind; sei es durch Gesundung oder aber durch den Tod. Jetzt kriegt man noch eine zusätzliche Gleichung ins Modell die beschreibt mit welcher Rate Menschen gesunden/sterben. Man kann natürlich auch die Genesenen und die Toten als unterschiedliche Gruppen betrachten; man kann eine Gruppe von Menschen einführen, die zwar schon infiziert sind aber die Krankheit noch nicht weitergeben; man kann berücksichtigen dass Menschen nach der Genesung erneut erkranken können (was im aktuellen Fall glücklicherweise nicht zu passieren scheint), und so weiter (wer wirklich mehr wissen will, kann sich in die Tiefen der Kermack–McKendrick-Theorie einarbeiten die in den 1920er Jahren von britischen Wissenschaftlern entwickelt worden ist).
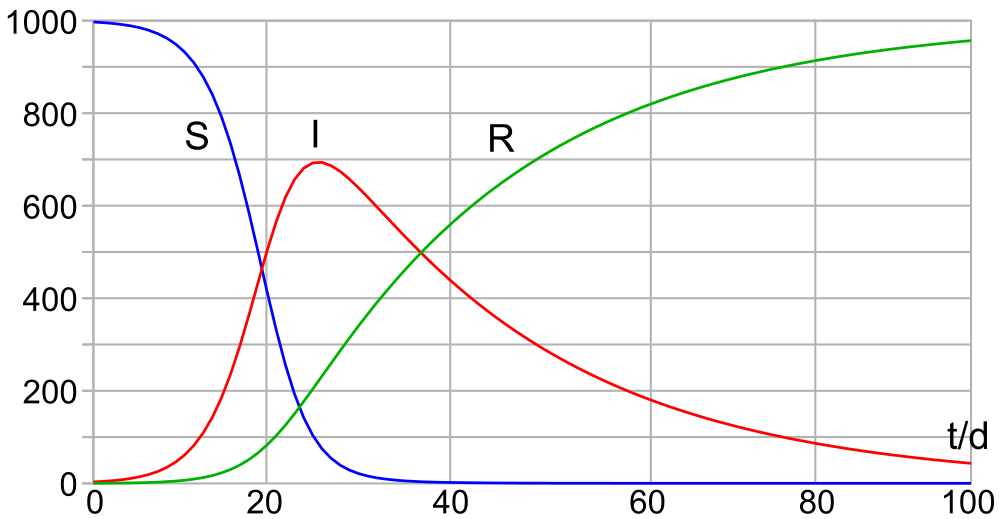
Typische Ergebnisse der Berechnung in einem SIR-Modell. Die Kurve, die wir “flatten” wollen ist die rote mit dem “I”. In dem Fall hat das Beispiel aber nix mit Corona zu tun sondern ist nur ein Beispiel (Bild: Klaus-Dieter Keller, gemeinfrei)
Am Ende kriegt man auf jeden Fall eine mehr oder weniger komplexe Anordnung von Differentialgleichung, die auf die eine oder andere Art zu lösen sind wenn man wissen will wie sich die Krankheit ausbreitet. Und hier ist auch die erste Gemeinsamkeit mit der Astronomie, denn selbsverständlich läuft auch hier alles über Differentialgleichungen. Was nicht überraschend ist, denn eine Differentialgleichung ist ja nichts anderes als eine Formel die angibt wie sich eine Größe ändert wenn sich gleichzeitig eine andere ändert. In der Astronomie will man zum Beispiel wissen wie sich die Position von Planeten ändert, was von der auf sie wirkenden Gravitationskraft anderer Himmelskörper abhängt, deren Position sich aber ja auch ändert. In der Epidemiologie hat man die sich verändernde Anzahl der Menschen in den verschiedenen Gruppen die bestimmt, wie sich diese Menge in Zukunft ändern wird.
In der Astronomie bin ich mit dem Aufstellen der Differentialgleichung quasi fertig. Ich muss mir dann “nur” noch eine vernünftige Methode überlegen sie auch am Computer lösen zu können. Wer gerne wissen will wie man das konkret macht kann gerne die Serie lesen, die ich vor langer Zeit einmal dazu geschrieben habe: Teil 1, Teil 2, Teil 3, Teil 4. In der Welt der Viren und der Menschen ist die Sache aber noch lange nicht zu Ende. Denn es reicht nicht zu wissen, wie sich so eine Krankheit rein mathematisch ausbreiten wird. Wir wollen es konkret wissen: Was passiert, wenn alle Schülerinnen und Schüler zuhause bleiben? Was passiert, wenn wir die Anzahl der engen Kontakte zwischen Menschen um 20 Prozent verringern? Um 50 Prozent? Was passiert, wenn die Theater 5 Wochen lang geschlossen bleiben und was, wenn die Schwimmbäder erst im Juni öffnen statt im Mai?
Um diese Fragen zu beantworten braucht es noch eine ganz andere Art von Computermodell. Und muss sich von der reinen Mathematik der Differentialgleichungen ab- und den etwas unordentlicheren Gebiete der Statistik und Soziologie zuwenden. Die Wissenschaftlerinnen und Wissenschaftler der TU Wien von denen das Diagramm ganz am Anfang stammt haben das in einem kurzen Dokument (pdf) ausführlich dargestellt. Es geht um “agentenbasierte Simulationsmodell” – was aber nichts mit Spionen zu tun hat die durch die Gegend laufen, die Bevölkerung bespitzeln und schauen wer gerade besonders heftig hustet.
Die “Agenten” sind das, was im Computermodell die Menschen repräsentiert. In der Astronomie habe ich ja auch keine ausgewachsene Planeten im Computer nachgebaut. Mein simulierter Mars ist ebenso ein simpler Punkt wie mein simulierter Jupiter, dass der eine eine eisige Staubwüste mit coolen Kratern und riesigen Vulkanbergen ist, spielt ebenso keine Rolle wie die beeindruckenden Wolkenbänder des Jupiters. Ich muss nur wissen, welche Masse die Dinger haben, denn die ist es ja, die für die Gravitationskraft und damit für die Bewegung verantwortlich ist. Genauso muss man natürlich nicht alle Eigenschaften aller Menschen simulieren die im Computermodell die Ausbreitung der Krankheit simulieren. Die Grundlage der Epidemie-Modelle der TU Wien bildet ein “individuenbasiertes Populationsmodell” namens GEPOC (über das man hier im Detail nachlesen kann: “GEPOC ABM: A generic agent-based population model for Austria”). Ganz vereinfacht gesagt: In diesem Modell “leben” jede Menge Menschen. Diese Menschen haben ein konkretes Alter und können weiblich oder männlich sein (was in diesem Fall nur heißt, dass sich manche “Agenten” fortpflanzen können und manche nicht). Die Menschen können sterben oder auswandern. Zu Beginn der Simulation schaut man natürlich darauf, dass die Population im wesentlich dem entspricht, was man simulieren will; das also die Zu- und Abwanderungsraten; die Geburts- und Sterberaten halbwegs der Realität entsprechen. Danach geht man der Reihe nach alle Agenten durch wobei die Reihenfolge vom Zufall bestimmt wird und bestimmet – ebenfalls per Zufall (aber anhang der entsprechenden realen Daten) – ob der Agent stirbt, auswandert oder einen neuen Agenten erschafft (d.h. Nachwuchs bekommt). Der Todes-, Geburts- und Auswanderungszeitpunkt wird ebenfalls per Zufall bestimmt und wenn das alles durch ist, wird das Modell aktualisiert. Die toten und ausgewanderten Agenten werden aussortiert; die neue geborenen Agenten kommen ins System dazu und erhalten per Zufall ein Geschlecht.

Je weniger Kontakte (rechts) desto langsamer breitet sich die Krankheit aus (Bild: TU Wien/dwh)
Soweit hat das alles noch nicht viel mit der Corona-Epidemie zu tun. Aber wenn man die Auswirkungen auf die Bevölkerung kennen will, braucht man natürlich zuerst einmal eine Bevölkerung mit der man simulieren kann. Diese Grundlage kann man nun erweitern. Zum Beispiel in dem man die Leute irgendwo wohnen lässt, sie also auch geografisch zuordnet. Und im konkreten Fall muss man natürlich auch die Kontakte zwischen den Agenten beschreiben. Wer trifft wie oft wie viele andere Menschen in welchen Zusammenhängen? Das kann man nun wirklich nicht mehr rein mathematisch lösen; dazu braucht man konkrete Daten. Die man entsprechend erheben muss. Was nichts anderes heißt als das man ausreichend viele echte Menschen ausreichend lange und intensiv befragt und ihre Kontakte aufzeichnet. Zum Glück gibt es auch Wissenschaftlerinnen und Wissenschaftler die genau das tun. Zum Beispiel in dieser Arbeit – “Social Contacts and Mixing Patterns Relevant to the Spread of Infectious Diseases” – in der 7290 Menschen aus acht europäischen Ländern untersucht und 97.904 Kontakte aufgezeichnet worden sind. Solche Daten kann man benutzen um die Interaktion der Agenten zu modellieren und genau das haben die Forscherinnen und Forscher der TU Wien getan.
Dazu wurde – jetzt im Fall der Stadt Wien – die Geografie in entsprechende Bereiche aufgeteilt. Es gibt Haushalte, Schulen (für alte und junge Kinder), Arbeitsstätten und Orte an denen man seine Freizeit verbringt. Dazu kommen Kinderbetreuungseinrichtungen, Einrichtungen für ältere Menschen und Orte an denen Großveranstaltungen stattfinden. Aus den bekannten und erhobenen Kontaktdaten und dem dynamischen Bevökerungsmodell wird nun simuliert welche Agenten in Abhängigkeit ihres Alters, Geschlechts, und so weiter wie viel Zeit an den entsprechenden Orten verbringen. Und DAS wird nun mit den mathematischen Modellen zur Ausbreitung der Virusepidemie kombiniert von denen ich zu Beginn erzählt habe. Man kann nun also einerseits in der Simulation verfolgen wie lange sich die Agenten an den unterschiedlichen Orten aufhalten und wie viele andere Agenten sie dort treffen. Und andererseits berechnen wie viele davon sich bei solchen Kontakten infizieren und die Infektion im Laufe der Zeit weiterverbreiten. Dann kann man im Modell die entsprechenden politischen Maßnahmen simulieren. Wenn die Schulen gesperrt sind, dann können die Kinder dort nicht mehr hin. Werden aber dafür vermehrt zuhause sein oder vielleicht auch an den Freizeit-Orten. Man kann simulieren wie sich verstärktes Home-Office auswirkt, in dem man die Zahl der Arbeitsstätten verringert, und so weiter.
In der Praxis ist das alles natürlich noch deutlich komplexer als ich es dargestellt habe. Aber man hat vielleicht zumindest einen kleinen Eindruck davon bekommen, wie all die Diagramme entstehen die momentan unser Leben bestimmen. Ein paar relevante Punkte muss man aber auf jeden Fall noch anmerken. Wenn ich in einer himmelsmechanischen Simulation die Bewegung der Planeten modelliere, dann kann ich mir ziemlich sicher sein, dass die modellierte Zukunft auch genau so eintreffen wird. Die Naturgesetze die die Bewegung der Himmelskörper bestimmen sind bekannt. Und die Himmelskörper halten sich daran, sie können nicht anders. Ein Planet kann sich nicht einfach entscheiden mal aus Spaß an der Freunde irgendwo anders hin zu fliegen. Meine Simulation wird nur dann fehlerhaft sein, wenn ich entweder selbst einen Fehler gemacht habe oder aber wenn ich zu sehr vereinfacht habe. Ich werde zum Beispiel keine brauchbaren Daten über die Bewegung des Mondes bekommen wenn ich nicht auch die Erde in meiner Simulation inkludiere. Ansonsten aber kann ich mich darauf verlassen, dass das eintritt was im Modell passiert. Und wir verlassen uns ja auch darauf: Wenn eine Raumsonde zum Mars fliegt, dann schicken wir sie an einen Ort, an dem der Mars zum Zeitpunkt des Starts noch gar nicht ist. Wir haben im Modell simuliert wo er sein wird, wenn die Sonde landet und die Simulation stimmt so exakt mit der Realität überein, dass die Sonden dann auch genau dort landen wo sie sollen.
Viren sind wie Wetter. Fast. Na ja, eigentlich gar nicht. (Bild: NOAA, gemeinfrei)
Bei den Modellen der Epidemiologen ist das anders. Menschen können sich entscheiden sich plötzlich anders zu verhalten als zuvor! Man kann das vielleicht besser mit Wettervorhersagen vergleichen: Da können wir für ein paar Tage ziemlich genau prognostizieren was passieren wird. Aber weil das ganze so enorm komplex ist, kann sich darüber hinaus alles sehr schnell ändern. Die Grafik die ich ganz zu Beginn gezeigt habe, macht Vorhersagen über einen Zeitraum von mehreren Monaten. Deren Gültigkeit hängt erstens von den vorhandenen Daten ab: Wie lang ist die Inkubationszeit, wie groß die Ansteckungsrate, wie hoch die Sterblichkeit, und so weiter. Das sind Daten, die wir derzeit noch nicht exakt kennen; wir erfoschen die Covid-19-Pandemie ja immer noch und die Parameter auf denen die Simulation basiert ändern sich. Zweitens kommt es aber auch auf die Menschen an. Wenn die sich plötzlich anders verhalten, weil sie zum Beispiel verständlicherweise keine Lust mehr haben zuhause zu hocken, dann sind auch die entsprechenden Prognosen hinfällig.
Die mathematischen Modelle und Computersimulationen zur Ausbreitung der Covid-19-Pandemie werden uns in den nächsten Monaten mit Sicherheit begleiten. Sie werden uns dabei helfen, die Übersicht in der Krise zu behalten. Wann sie zu Ende sein wird, können sie zwar vorhersagen aber nur bedingt. Denn am Ende liegt es an uns selbst, wie schnell die Sache durchgestanden ist. Und natürlich an diesem fiesen kleinen Virus! Blödes Ding!











Kommentare (25)