Letzte Woche wurde der Physik-Nobelpreis 2020 verliehen. Die eine Hälfte haben Reinhard Genzel und Andrea Ghez bekommen. Sie haben die Bewegung von Sternen im Zentrum unserer Galaxie untersucht und so nachweisen können, dass die Sterne ein Objekt umkreisen, das nur ein gewaltiges schwarzes Loch sein kann. Ein sogenanntes “supermassereiches schwarzes Loch” das mehr als 4 Millionen mal mehr Masse als unsere Sonne hat. Was Genzel und Ghez dabei genau getan haben, habe ich letzte Woche schon genauer erklärt. Das war aber, wie gesagt, nur die eine Hälfte des Nobelpreises. Die andere Hälfte hat der britische Mathematiker und theoretische Physiker Roger Penrose bekommen. Und zwar “, für die Entdeckung, dass die Bildung Schwarzer Löcher eine robuste Vorhersage der Allgemeinen Relativitätstheorie ist”.
Das klingt spannend, es klingt wichtig und man kann sich nicht so wirklich etwas darunter vorstellen. Und tatsächlich IST es spannend, es IST enorm wichtig und leider IST es auch sehr schwer, die Forschung von Penrose anschaulich zu erklären. Es geht dabei um etwas, das “Singularitätstheorem” heißt und ich sage gleich dazu, dass ich weit davon entfernt bin, ein Experte auf diesem Gebiet zu sein. Ich werde also Penroses Arbeit nicht im Detail erklären können. Aber zumindest einen groben Überblick sollte ich schaffen.
Die Arbeit am Singularitätstheorem begann in den 1960er Jahren. Und nicht nur Roger Penrose alleine hat daran gearbeitet sondern auch Stephen Hawking (der, wenn er nicht schon tot wäre, jetzt also genau so mit einem Nobelpreis geehrt werden müsste). Aber eigentlich fängt die Geschichte noch ein bisschen früher an, nämlich im Jahr 1915 als Albert Einstein seine Allgemeine Relativitätstheorie veröffentlichte. Also seine wissenschaftliche Beschreibung der Art und Weise wie Raum, Zeit, Masse und Gravitation zusammenwirken, mit der überraschenden Erkenntnis dass Masse die Raumzeit krümmt, Objekte bei ihrer Bewegung durch den Raum dieser Krümmung folgen und wir diese Bewegung im gekrümmten Raum als Gravitationskraft wahrnehmen.

Sir Roger Penrose (Bild: Biswarup Ganguly, CC-BY 3.0)
Schon kurz nachdem Einstein die mathematischen Gleichungen veröffentlicht hatte, mit denen man beschreiben konnte wie Raum und Zeit sich unter dem Einfluss von Massen krümmen, fand der Physiker Karl Schwarzschild die erste exakte Lösung dafür. Allerdings eine Lösung mit einem Problem, nämlich einer “Singularität”. Vereinfacht gesagt bedeutet das, dass sich die Raumzeit unter Umständen so extrem krümmen kann, dass die Krümmung an einem Punkt unendlich groß wird. Betrachtet man zum Beispiel eine Masse – etwa einen kollabierenden Stern – der unter seinem eigenen Gewicht in sich zusammenfällt, wird im Laufe der Zeit immer mehr Masse auf immer kleinerem Raum konzentriert. Dieser Kollaps geht immer weiter, bis irgendwann die gesamte Masse in einem einzigen Punkt vereint ist. Man hat dann also einen Punkt mit einer unendlich großen Dichte und einer daraus folgenden unendlich großen Raumkrümmung. Genau das nennt man “Singularität” und genau die war das Problem.
Erstens, weil man sich nicht darüber im Klaren war, ob das wirklich eine Folge von Einsteins Theorie zur Beschreibung der Gravitation war. Oder vielleicht doch nur eine Folge diverser Vereinfachungen die Schwarzschild machen musste, um seine Lösung zu finden. Oder anders gefragt: Sind Singularitäten nur ein mathematisches Überbleibsel der Art und Weise wie Einsteins Gleichungen behandelt wurden; ein Überbleibsel das nichts mit der Realität zu tun hat und ignoriert werden kann? Oder stecken die Singularitäten direkt in Einsteins Gleichungen mit drin?
Genau das ist es, was Penrose und Hawking mit dem Singularitäten-Theorem untersucht haben. Die mathematischen Details dieser Arbeit übersteigen meine Fähigkeiten. Im Wesentlichen geht es aber darum, dass man bestimmte, sehr einfache und “logische” Bedingungen aufstellt. Zum Beispiel die, dass die Gravitation immer nur anziehend wirkt (und nicht sowohl anziehend als auch abstoßend wirken kann, wie zum Beispiel die elektromagnetische Kraft). Oder dass die Raumzeit “chronologisch” ist, also kein Ereignis in seiner eigenen Zukunft oder Vergangenheit liegt. Es gibt noch ein paar weiterer solcher Bedingungen, die aber alle nicht sonderlich extrem oder außergewöhnlich sind und bei denen man durchaus davon ausgehen kann, dass sie im Universum erfüllt sind. Wenn nun diese Bedingungen gelten, so Penrose und Hawking, dann führt Einsteins Allgemeine Relativitätstheorie zu Singularitäten. Eine Singularität ist also kein mathematische Absonderlichkeit die man ignorieren kann. Sondern folgt direkt aus Einsteins Gleichungen.
Bis jetzt habe ich das Wort “schwarzes Loch” noch nicht erwähnt. Aber daran kommt man natürlich nicht vorbei bei diesem Thema. Wenn ein großer, massereicher Stern am Ende seinses Lebens in sich zusammenfällt, dann wird er unter seinem eigenen Gewicht immer dichter und dichter. Ist die Masse groß genug, dann kennen wir keine Kraft, die diesen Kollaps aufhalten kann. Und dann passiert genau das, was nach Einstein, Penrose und Hawking passieren muss: Die gesamte Masse vereint sich in einem einzigen Punkt mit unendlich großer Dichte und unendlicher Raumkrümmung. Genau das hat das Nobelpreiskomitee gemeint, als es von der “Entdeckung, dass die Bildung Schwarzer Löcher eine robuste Vorhersage der Allgemeinen Relativitätstheorie ist” gesprochen hat.
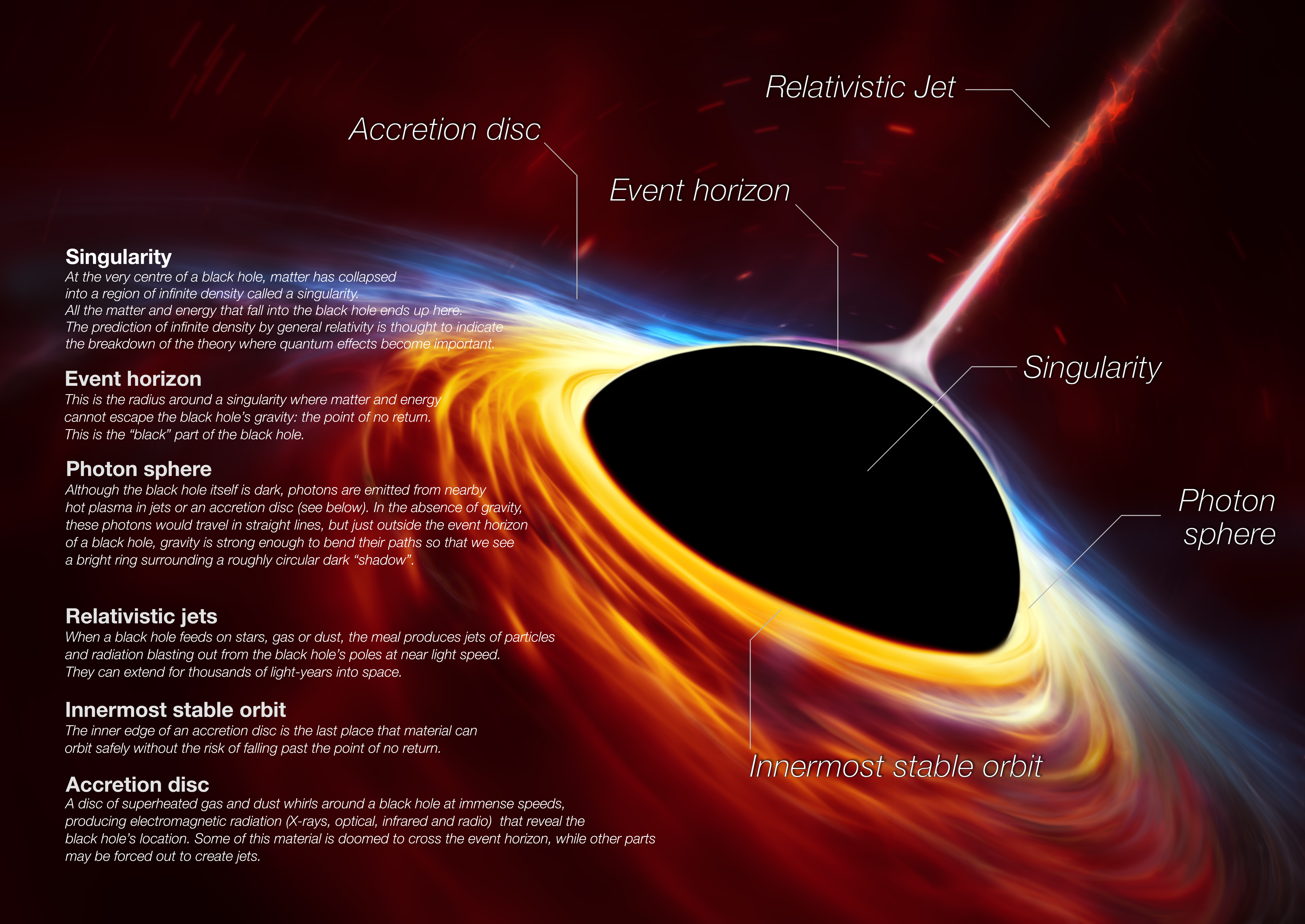
Aufbau eines schwarzen Lochs (Bild: ESO)
Die Geschichte ist damit aber noch nicht zu Ende. Das Singularitätstheorem funktioniert nicht nur bei schwarzen Löcher. Stephen Hawking konnte 1966 zeigen, dass es auch auf das ganze Universum anwendbar ist. Also: Dass unser Kosmos selbst in der Vergangenheit eine Singularität hat; also einem Zustand unendlich großer Dichte entsprungen ist. Hawking hat gezeigt, dass in der Vergangenheit des Universums ein “Urknall” zu finden sein muss (wie ich hier ein wenig ausführlicher erklärt habe). Die Arbeit von Penrose und Hawking (und all ihrer Kollegen) hat uns sehr viel sehr spektakuläre und verwirrende Erkenntnisse über die Natur von Raum und Zeit gebracht. Der Nobelpreis ist absolut verdient. Auch wenn es so etwas wie eine “Singularität” in der Realität nicht geben kann. Schwarze Löcher sind keine Singularitäten, zumindest dann nicht, wenn man den Begriff im obigen mathematischen wörtlichen Sinne verwendet. Es kann im Kosmos keine Punkte geben; also Objekte die keine räumliche Ausdehnung haben. Es kann darüber hinaus keinen Punkt geben, dessen Dichte unendlich groß ist. Unendlichkeiten dieser Art können nicht existieren; darüber sind sich so gut wie alle Forscherinnen und Forscher einig. Das hat Konsequenzen: Penrose und Hawking haben gezeigt, dass die Singularitäten direkt aus Einsteins Beschreibung der Gravitation folgt. Sie sind dort quasi fix eingebaut. Und wenn es keine Singularitäten geben kann, dann folgt daraus: Einsteins Beschreibung der Gravitation und der Raumzeit ist nicht vollständig. Wir haben irgendeinen Aspekt der Angelegenheit noch nicht vernünftig verstanden; irgendetwas, was dazu führt, dass die Singularität eben nicht Auftritt.
Kurzer Einschub: Das alles bedeutet nicht, dass schwarze Löcher nicht existieren können. Wenn wir ein schwarzes Loch nicht mit der Singularität gleichsetzen, sondern es als Region in der Raumzeit bezeichnen, aus der nichts entkommen kann, dann gibt es die Dinger definitiv. Wir haben sie >indirekt nachgewiesen und direkt beobachtet. Es braucht keine unendlich hohe Dichte und Raumkrümmung damit aus einer Region nichts mehr entkommen kann. Sie muss nur groß genug sein, denn umso größer sie ist, desto schneller müsste man sein um dieser extrem gekrümmten Region der Raumzeit entkommen zu können. Und wenn diese benötigte Geschwindigkeit größer als die Lichtgeschwindigkeit ist, dann bleibt alles darin für immer gefangen. Die Grenze, an der die Raumkrümmung groß genug ist, nennt man “Ereignishorizont” und alles was sich dahinter befindet, ist für das Universum außerhalb davon verloren.
Penrose hat auch jede Menge andere coole Sachen in der Mathematik erforscht – zum Beispiel Parkettierungen (Bild: gemeinfrei)
Solche “Ereignishorizont-Objekte” haben wir im Universum nachgewiesen; sie sind real. Die offene Frage betrifft das, was sich dahinter befindet. Irgendwas muss mit der Masse hinter dem Ereignishorizont ja passieren. Sie kann nicht einfach verschwinden. Die Relativitätstheorie sagt uns, dass sie zu einem unendlich dichten Punkt kollabiert, was falsch sein muss. Also folgt daraus, dass die Relativitätstheorie nicht ausreicht, um das zu beschreiben, was hinter dem Ereignishorizont passiert. Eine über die Relativitätstheorie hinausgehende Theorie haben wir allerdings noch nicht. Obwohl sich viele Forscherinnen und Forscher seit Jahrzehnten damit beschäftigen; inklusive Roger Penrose. Seine mathematische Arbeit hat zum Beispiel zur Entwicklung der Schleifenquantengravitation beigetragen, einer Hypothese die die Relativitätstheorie mit der Quantenmechanik verbinden und eine Beschreibung des Universums finden will, in der keine Singularitäten auftauchen. Penrose hat auch die sogenannte “Cosmic Censorship”-These aufgestellt, also die Behauptung, dass es keine “nackten Singularitäten” geben kann. So eine “nackte Singularität” ist genau das, von dem ich vorhin gesprochen habe, ein Punkt der Raumzeit mit unendlicher Krümmung der NICHT von einem Ereignishorizont umgeben ist. Ob Penrose mit dieser Hypothese recht hat, ist nicht klar. Je nach mathematischem Modell lautet die Antwort mal “Ja” und mal “Nein” – solange wir keine Theorie haben, die über Einsteins Allgemeine Relativitätstheorie hinaus geht, werden wir wohl auch keine definitive Antwort bekommen.












Kommentare (22)