Es gibt keine Schwerkraft, sondern nur die Raumzeitkrümmung – das haben wir im letzten Teil gesehen. Deshalb lohnt es sich, zum Abschluss noch einmal einen Blick auf die Raumzeitkrümmung zu werfen, also auf die Metrik.
Ihr erinnert euch noch an Teil II und Teil III? Dort haben wir gesehen, dass Geodäten zeigen, ob ein Raum gekrümmt ist: Laufen zwei Geodäten immer aufeinander zu, dann ist die Krümmung positiv, laufen sie voneinander weg, dann ist sie negativ.
Geodäten über der Erde
Geodäten in der Raumzeit sind die Weltlinien von Teilchen, die kräftefrei sind (dran denken: Schwerkraft gibt es nicht) und nur der Raumzeitkrümmung folgen. Als erstes lassen wir drei Teilchen in einer Erdumlaufbahn starten, die alle den gleichen Abstand von der Erde haben. Die Anfangsgeschwindigkeit der Teilchen ist Null, sie fallen also einfach auf die Erde zu (Bild zum Vergrößern anklicken):
Dabei habe ich die Erde zweidimensional gezeichnet, damit ich die dritte Dimension für die Zeit nehmen kann. Ich habe ein Koordinatensystem mit Ursprung im Zentrum der Erde mitgezeichnet; das wird später noch hilfreich werden. Ein Wort der Warnung: Dieses und die folgenden Bilder sind nicht maßstabsgetreu.
Was passiert mit unseren Teilchen? Sie beschleunigen auf die Erde zu, und zwar alle um denselben Betrag. Weil sie von Außen kommen, nähern sie sich dabei einander an. In dieser Richtung ist die Raumzeit also positiv gekrümmt.
Als nächstes starten wir die drei Teilchen mit unterschiedlicher Entfernung zur Erde. Das nächste Teilchen wird, weil es dichter an der Erde ist, stärker beschleunigt, das am weitesten entfernte Teilchen am wenigsten. Entsprechend laufen die Geodäten auseinander:
Die Raumzeit hat also auch einen negativen Krümmungsanteil.
Man kann beide Bilder zusammenfassen, indem man sich anschaut, was aus einem Kreis aus Teilchen wird: Der wird in der einen Richtung gelängt, in der anderen gestaucht:
Wenn der Kreis ein materielles Objekt wäre, dann würde er sich also verformen. Für den Kreis würde es so aussehen, als würde die Seite, die näher zur Erde ist, stärker angezogen, die Seite, die am weitesten weg ist, schwächer. Kommt euch sowas bekannt vor? Richtig, wir haben gerade die Gezeiten wiederentdeckt (bei denen ist es natürlich die Erde, deren Ozeane in der Raumkrümmung des Mondes verzerrt werden):
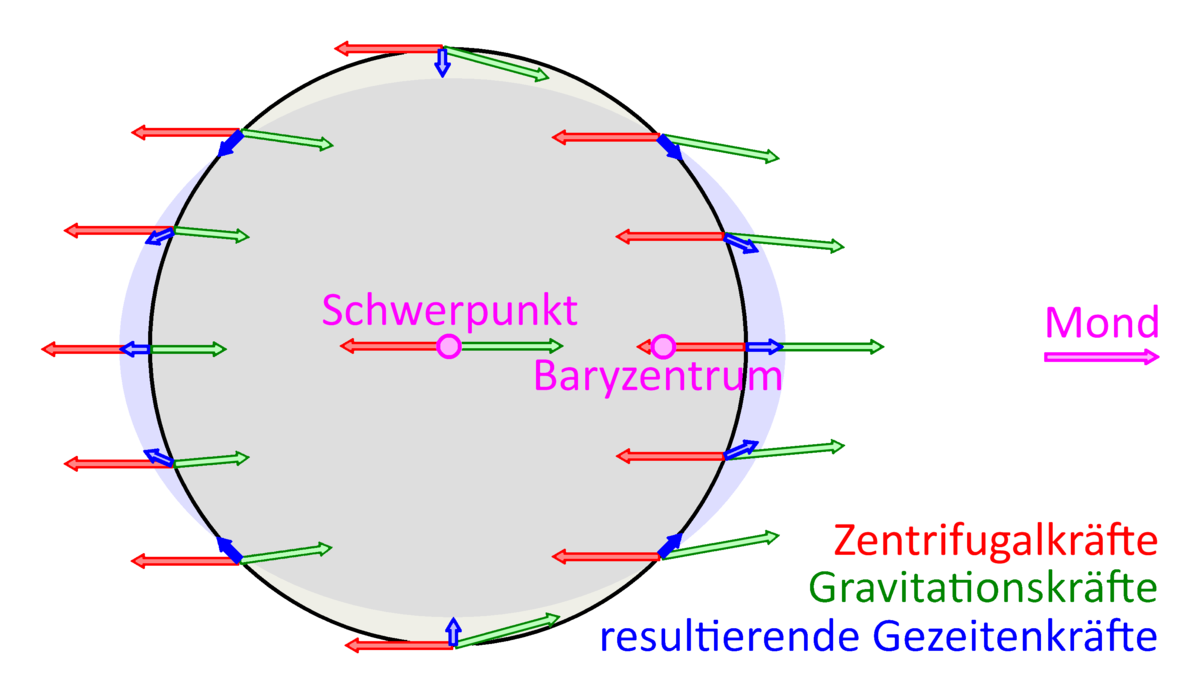
Von de:Benutzer:Dringend, bearbeitet von Lämpel – eigene Skizze, CC BY-SA 3.0 de, Link
Bild wie immer von Wikipedia [hier war früher ein anderes bild, das hatte aber Copyrightprobleme…] – allerdings dort ganz klassisch mit “Kräften” erklärt, statt richtig mit der Raumzeitkrümmung. Die Raumzeitkrümmung erklärt auch vollkommen zwanglos und stressfrei, warum es zwei Flutberge geben muss – der Kreis wird zur Ellipse verzerrt, nicht zu einem Ei.
Letztes Mal hatte ich ja behauptet, dass man ein “Schwerefeld” und eine Beschleunigung in einer Rakete nicht voneinander unterscheiden kann. Das gilt allerdings nur, wenn man ein sehr kleines Labor hat – wenn das Labor groß genug ist, dann könnte man Gezeiteneffekte sehen, die es in einer beschleunigten Rakete nicht gibt. (Das ist allerdings kein Widerspruch zum Äquivalenzprinzip – man kann sich nämlich auch ein vollkommen homogenes Schwerefeld über einer massiven Platte vorstellen, bei dem gibt es keine Gezeiten.)
Gezeiteneffekte machen es also möglich, die Krümmung der Raumzeit sichtbar zu machen. Unser Kreis wird beispielsweise zur Ellipse verzerrt. Da er in einer Richtung länger, in der anderen kürzer wird, können wir sehen, dass die mittlere Krümmung der Raumzeit gerade gleich Null ist. Das muss auch so sein, denn eine nicht verschwindende mittlere Krümmung der Raumzeit gibt es nur da, wo Materie ist (also beispielsweise im Inneren der Erde).
Die Raumkrümmung im Erdinnern
Die Bilder von oben gelten außerhalb der Erde. Im Erdinnern sieht die Raumkrümmung anders aus. (Ich nehme hier der Einfachheit halber an, dass die Erde eine perfekte Kugel mit konstanter Dichte ist.)






Kommentare (115)